0%

Cpp基础（5）函数

发表于 更新于 分类于 本文字数： 12k
复习了C++中函数的内容

函数基础

函数的定义和声明

函数是C++程序的基本构成单元，一个C++程序由一个或多个源文件组成，一个源程序文件可以由一个或多个函数组成。一个典型的函数（function）定义包括：返回类型（return type）、函数名字、由0个或多个形参（parameter）组成的列表以及函数体。函数执行的操作在语句块，称为函数体。

1
2
3
4
5
6
7
8
//计算阶乘
int fact(int val)
{
    int ret = 1;
    while (val > 1)
        ret* = val--;
    return ret;
}

函数的类型是指函数返回值的数据类型，若函数类型与return语句中表达式的值不一致，则以函数类型为准，系统自动进行类型转换。

1
2
3
4
int bigger(float x, float y)
{
    return (x > y ? x : y);   //返回时会转换为整数
}

函数的名字也必须在使用之前声明，函数只能定义一次，但可以声明多次。函数的声明不包含函数体，所以也就无须形参的名字，但是加上便于理解。函数声明也称作函数原型（function prototype）。

建议变量在头文件中声明，在源文件中定义。与之类似，函数也该在头文件中声明而在源文件中定义。这样可以确保同一函数的所有声明保持一致。定义函数的源文件应该把含有函数声明的头文件包含进来，编译器负责验证函数的定义和声明是否匹配。

需要注意的是：函数不能嵌套定义，函数间可以互相调用，但不能调用main函数。

函数的调用

函数的调用完成两项工作：一是用实参初始化函数对应的形参，二是将控制权转移给被调用函数。此时主调函数（calling function）的执行被暂时中断，被调函数（called function）开始执行。执行函数的第一步是（隐式地）定义并初始化它的形参。当遇到一条return语句时函数结束执行过程，return语句也完成两项工作：一是返回return语句中的值（如果有的话），二是将控制权从被调函数转移回主调函数。

1
2
3
4
5
6
int main()
{
    int j = fact(5);
    cout << "5! is" << j << endl;
    return 0;
}

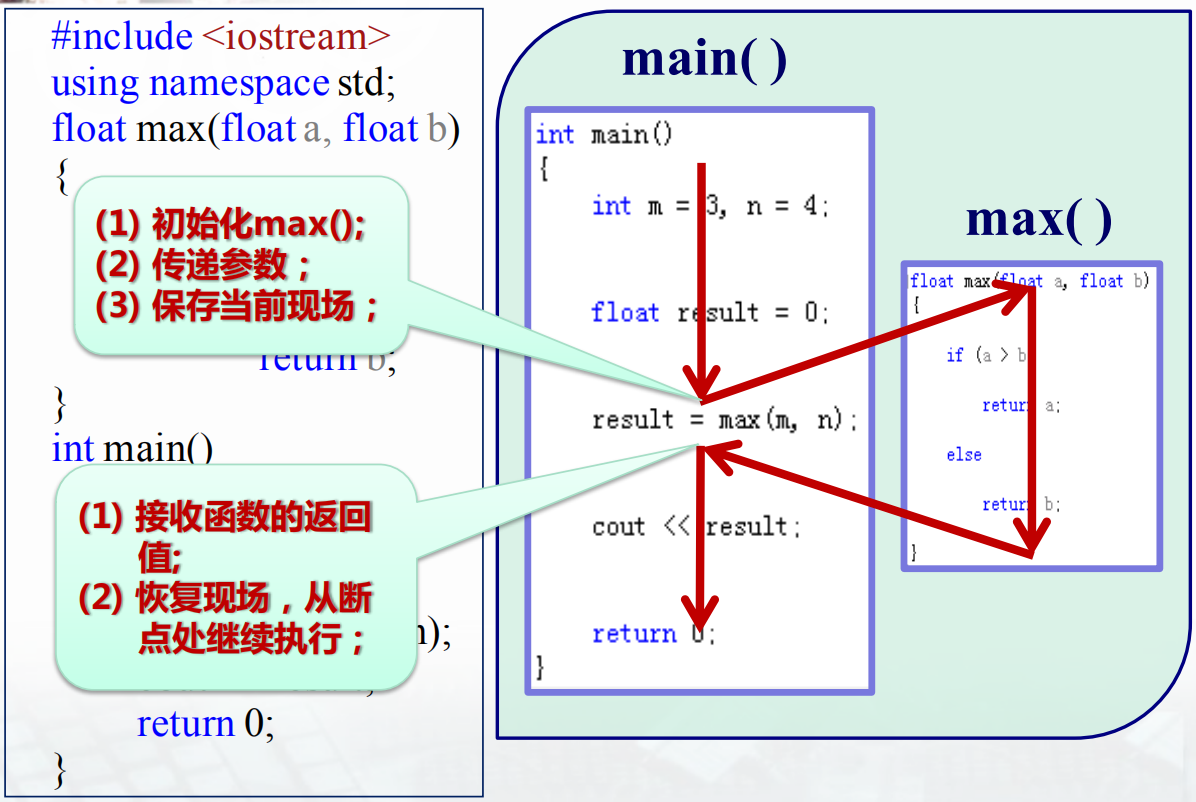
QQ图片20200130201451

一个函数调用的执行过程可以分为3个阶段：

  1. 首先把实参值传入被调用函数形参的对应单元中，中断主调函数当前的执行，并且保存返回地点（称为断点）。
  2. 执行被调用函数语句，直到return语句返回。若被调用函数中没有return语句，则直到其全部语句执行完毕后自动返回到位于主调函数中的断点处。
  3. 从保存的断点处，主调函数继续执行其他剩余语句。

形参和实参

实参是形参的初始值，编译器能以任意可行的顺序对实参求值。实参的类型必须与对应的形参类型匹配。实参与形参具有不同的存储单元，实参与形参变量的数据传递是“值传递”（passed by value）；函数调用时，系统给形参分配存储单元，并将实参对应的值传递给形参。

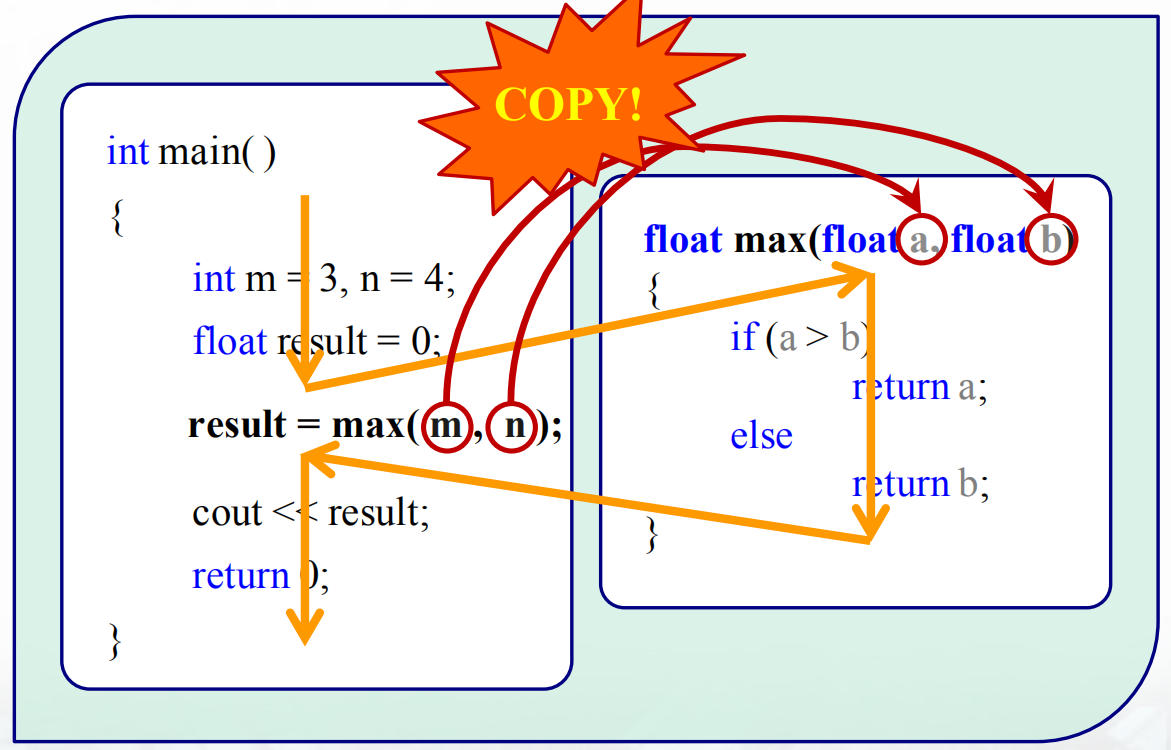
QQ图片20200130202050

函数的形参列表可以为空，但是不能省略，其中每个形参都是含有一个声明符的声明，即使两个形参的类型一样，也必须把两个类型都写出来，且任意两个形参都不能同名，

函数的返回类型不能是数组类型或函数类型，但可以是指向数组或函数的指针。一种特殊的返回类型是void，它表示函数不返回任何值。

变量的作用范围

根据变量在程序中作用范围的不同，可以将变量分为：

局部变量：在函数内或块内定义，只在这个函数或块内起作用的变量；

全局变量：在所有函数外定义的变量，它的作用域是从定义变量的位置开始到本程序文件结束。

当全局变量与局部变量同名时，局部变量将在自己作用域内有效，它将屏蔽同名的全局变量，即在局部变量的作用范围内，全局变量不起作用。

需要注意的是，不在必要时不要使用全局变量。因为全局变量在程序的全部指向过程中都占用存储单元；过多地使用全局变量，程序的可读性变差；会增加函数之间的“关联性”，降低了函数的独立性，使函数可移植性降低。

QQ图片20200130204440

自动对象与局部静态对象

对于普通局部变量对应的对象来说，当函数的控制路径经过变量定义语句时创建该对象，当到达定义所在的块末尾时销毁它，把只存在于块执行期间的对象称为自动对象（automatic object）。

形参是一种自动对象，我们用传递给函数的实参初始化形参对应的自动对象。对于局部变量对应的自动对象，分为两种情况：如果变量定义本身含有初始值，就用这个初始值进行初始化；否则，如果变量定义本身不含初始值，执行默认初始化。

有时局部变量的生命周期贯穿函数调用及之后的时间，可以将局部变量定义为static类型。局部静态对象（local static object）在程序的执行路径第一次经过对象定义语句时初始化，并且直到程序终止才被销毁。

1
2
3
4
5
6
7
8
9
10
11
12
//下面的函数统计它自己被调用了多少次
size_t count_calls()
{
    static size_t ctr = 0;
    return ++ctr;
}
int main()
{
    for (size_t i=0; i!=10; ++i)
        cout << cout_calls() << endl;
    return 0;
}

指针形参

指针用做函数参数，在函数内部改变指针的值只能改变局部变量，不会影响实参原来的值；在函数内部通过解引用操作改变指针所指内容的值，即实参指针所指内容的值也发生了改变。

例子：编写一个函数，使用指针形参交换两个整数的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
using namespace std;
void mySWAP(int *p, int *q)
{
	int tmp = *p;
	*p = *q;
	*q = tmp;
}

int main()
{
	int a = 5, b = 10;
	int *r = &a, *s = &b;
	cout << "交换前：a=" << a << "，b=" << b << endl;
	mySWAP(r, s);
	cout << "交换后：a=" << a << "，b=" << b << endl;
	return 0;
}

1

需要注意的是，下面的函数并不能满足要求，因为在函数内部改变指针的值（改变指针所指的地址）只能改变局部变量。

1
2
3
4
5
6
void mySWAP(int *p, int *q)
{
	int *tmp = p;
	p = q;
	q = tmp;
}

引用形参

我们知道对于引用的操作实际上是作用在引用所引的对象上。引用形参的行为与之类似。

与值传递（实参的值被拷贝给形参，形参和实参是两个相互独立的变量）不同的是，引用形参是传引用的方式，形参是对应的实参的别名，形参绑定到初始化它的对象，如果改变了形参的值，也就是改变了对应实参的值。

用引用形参重写上面例子中的程序，引用形参绑定初始化它的对象，p绑定我们传给函数的int对象a，改变p的值也就是改变p所引对象的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
using namespace std;
void mySWAP(int &p, int &q)
{
	int tmp = p;
	p = q;
	q = tmp;
}

int main()
{
	int a = 5, b = 10;
	cout << "交换前：a=" << a << "，b=" << b << endl;
	mySWAP(a, b);
	cout << "交换后：a=" << a << "，b=" << b << endl;
	return 0;
}

QQ图片20200131142122

使用引用形参避免拷贝

拷贝大类类型对象或者容器对象比较低效，甚至有的类类型不支持拷贝。当某种类型不支持拷贝操作时，函数只能通过引用形参访问该类型的对象。

如果函数无须改变引用形参的值，最好将其声明为常量引用。把函数不会改变的形参定义成（普通的）引用是一种比较常见的错误，这么做有几个缺陷：一是容易给使用者一种误导，即程序允许修改变量s的内容；二是限制了该函数所能接受的实参类型，我们无法把const对象、字面值常量或者需要进行类型转换的对象传递给普通的引用形参。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//比较两个string 对象的长度
bool isShorter(const string &s1, const string &s2)
{
    return s1.size() < s2.size();
}

//判断一个string对象是否含有大写字母
bool HasUpper(const string &str)  //无须修改参数的内容，设为常量引用类型
{
    for (auto c : str)
        if(isupper(c))
            return true;
    return false;
}

//把字符串的所有大写字母转成小写
void ChangeToLower(string &str)
{
    for (auto &c : str)
        c = tolower(c);
}

使用引用形参返回额外信息

一个函数只能返回一个值，然而有时函数需要同时返回多个值，引用形参为一次返回多个结果提供了有效的途径。（对于引用的操作实际上是作用在引用所引的对象上）

例子：定义一个名为find_char的函数，返回string对象中某个指定字符第一次出现的位置，同时能“返回”该字符出现的次数。

一种思路是定义一个新的数据类型，包含位置和数量两个成员，显然比较复杂；另一种更简单的方法是，给函数传入一个额外的引用实参。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
string::size_type find_char(const string &s, char c, string::size_type &occurs)
{
    auto ret = s.size();
    occurs = 0;
    for (decltyoe(ret) i = 0; i!=s.size(); i++)
    {
        if(s[i] == c)
        {
            if(ret == s.size())
                ret = i;         //记录c第一次出现的位置
            ++occurs;
        }
    }
    return ret;                 //出现次数通过occurs隐式地返回
}

数组形参

数组有两个特殊性质：不允许拷贝数组，以及使用数组时通常会将其转换成指针。所以我们不能以值传递的方式使用数组参数，当我们为函数传递一个数组时，实际上传递的是指向数组首元素的指针。

尽管不能以值传递的方式传递数组，但是我们可以把形参写成类似数组的形式：

1
2
3
4
//这三个print函数是等价的
void print(const int*);
void print(const int[]);
void print(const int[10]);

当编译器处理对print函数的调用时，只检查传入的参数是否是const int*类型；如果我们传给print函数的是一个数组，则实参自动地转换成指向数组首元素的指针，数组的大小对函数的调用没有影响。以数组为形参的函数也必须确保使用数组时不会越界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<iostream>
using namespace std;
void sum(int *p, int n)
{
    int total = 0;
    for (int i=0; i<n; i++)
    {
        total+=*p++;
    }
    cout << total << endl;
}
int main()
{
    int a[10] = {1,2,3,4,5,6,7,8,9,10};
    sum(a,10);
    return 0;
}

多维数组名做函数参数

当将多维数组传递给函数时，真正传递的是指向数组首元素的指针，而多维数组的首元素是一个数组，指针就是一个指向数组的指针。数组第二维（以及后面所有维度）的大小都是数组类型的一部分，不能省略。

1
2
3
//这两个print等价
void print(int (*matrix)[10], int rowSize);   //（*matrix)的括号不能少
void print(int matrix[][10], int rowSize);

例子：求一个$3\times 4$的矩阵的所以元素中的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int maxvalue(int (*p)[4])
{
    int max = p[0][0];
    for(int i=0; i<3; i++)
        for(int j=0; j<4; j++)
            if(p[i][j] > max)
                max = p[i][j];
    return max;
}
int main()
{
    int a[3][4] = {{1,3,5,7},{9,11,13,15},{2,4,6,8}};
    cout << "The Max value is" << maxvalue(a);
    return 0;
}

数组引用形参

形参也可以是数组的引用，此时引用形参绑定到对应的实参上，也就是绑定到数组上。但此时函数只能作用于固定大小的数组。

1
2
3
4
5
void print(int (&arr)[10])    //只能将函数作用于大小为10的数组，(&arr)的括号不能少
{
    for(auto elem : arr)
        cout << elem <<endl;
}

函数的递归

什么是递归

我们已经知道：函数不能嵌套定义，函数可以嵌套调用。那么一个函数能调用“自己”嘛？答案是可以的

例子：已知 n，求n的阶乘$n!$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<iostream>
using namespace std;
int fact(int n)
{
    if(n==1)
        return 1;
    else 
        return n*fact(n-1);     //每次调用，数据规模缩小
}
int main()
{
    cout << fact(4) <<endl;
    return 0;
}

深入理解递归的过程

递归调用与普通调用在实质上是一样的。

QQ图片20200201100341

通过下面的两个例子来理解递归的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
using namespace std;
int recur()
{
	char c;
	c = cin.get();
	if (c != '\n')
		recur();
	cout << c;
	return 0;
}
int main()
{
	recur();
	return 0;
}

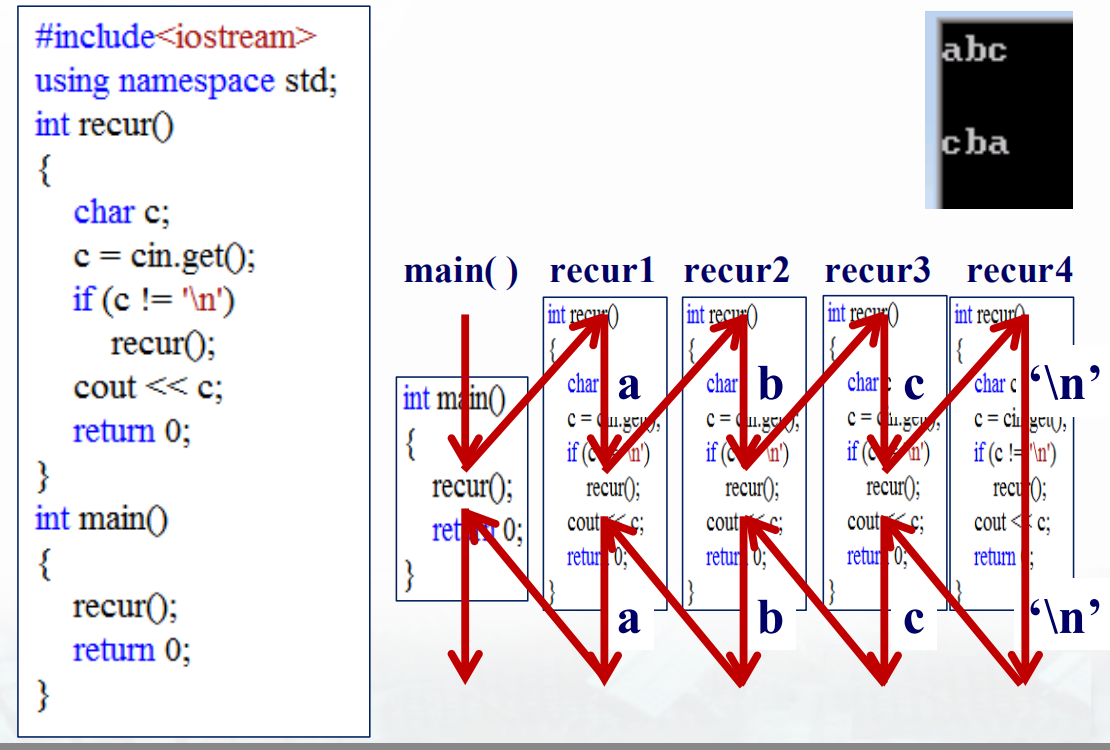
QQ图片20200201100347

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
using namespace std;
int recur()
{
	char c;
	c = cin.get();
	cout << c;
	if (c != '\n')
		recur();
	return 0;
}
int main()
{
	recur();
	return 0;
}

QQ图片20200201100351

递归的作用

用递归来完成递推

递归的关注点放在求解目标上，重在表现第i次与第i+1次的关系，让程序变得简明。必须要确定第1次的返回结果。

例子：斐波那契数列

1
2
3
4
5
6
7
8
9
int f(int n)
{
    if(n == 1)
        return 1;
    if(n == 2)
        return 1;
    else
        return(f(n-1)+f(n-2));  
}

模拟连续发生的动作

主要是搞清楚连续发生的动作是什么；搞清楚不同动作之间的关系；搞清楚边界条件是什么。

例子1：将一个十进制整数转换成二进制数

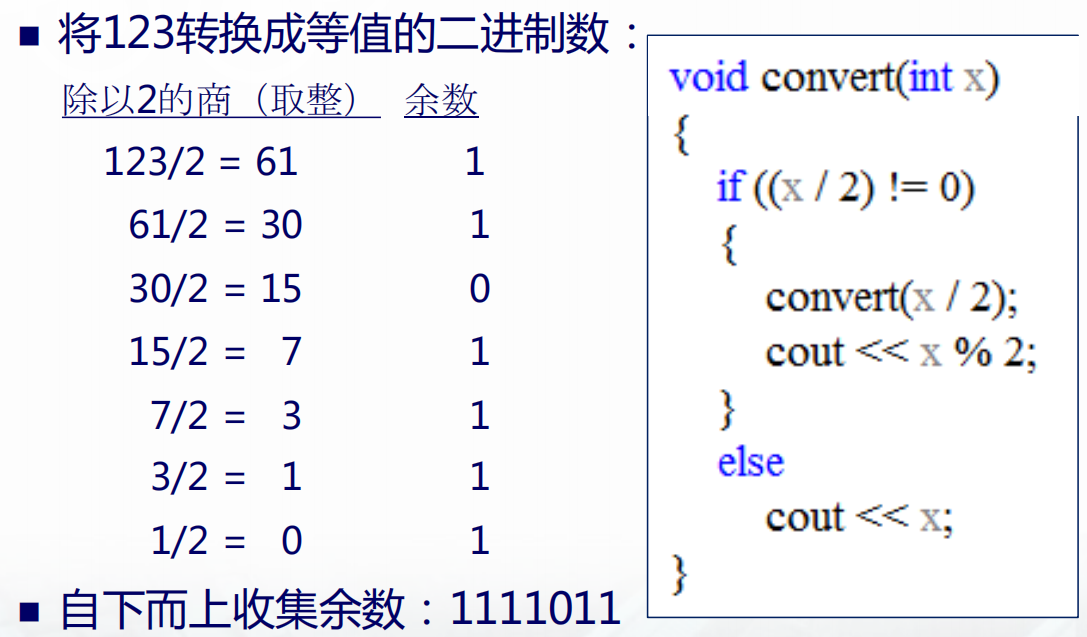
QQ图片20200201110807

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<iostream>
using namespace std;
void convert(int x)
{
	if ((x / 2) != 0)
	{
		convert(x / 2);
		cout << x % 2;
	}
	else
		cout << x;
}
int main()
{
	int x;
	cin >> x;
	convert(x);
	return 0;
}

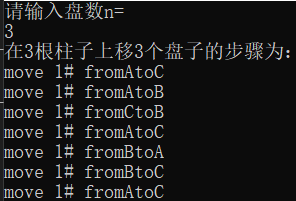
例子2：汉诺塔问题

相传在古代印度有位僧人整天把三根柱子上的金盘倒来倒去，他想把64个一个比一个小的金盘从一根柱子上移到另一个柱子上去。移动过程中恪守下述规则：每次只允许移动一只盘，且大盘不得落在小盘上面。

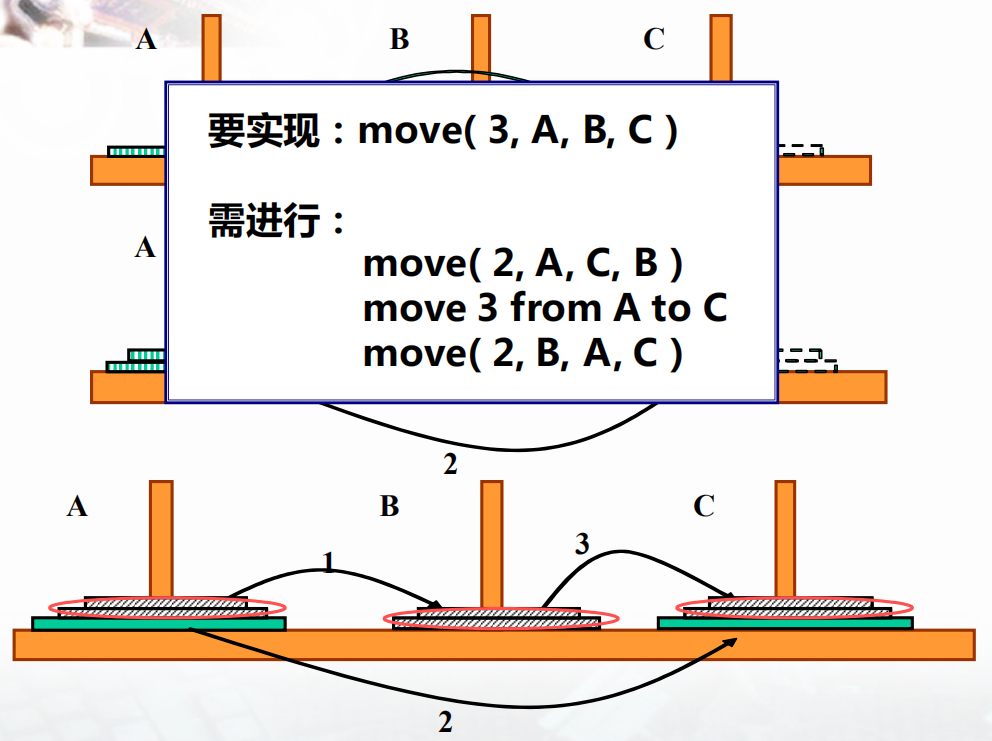
QQ图片20200201112556

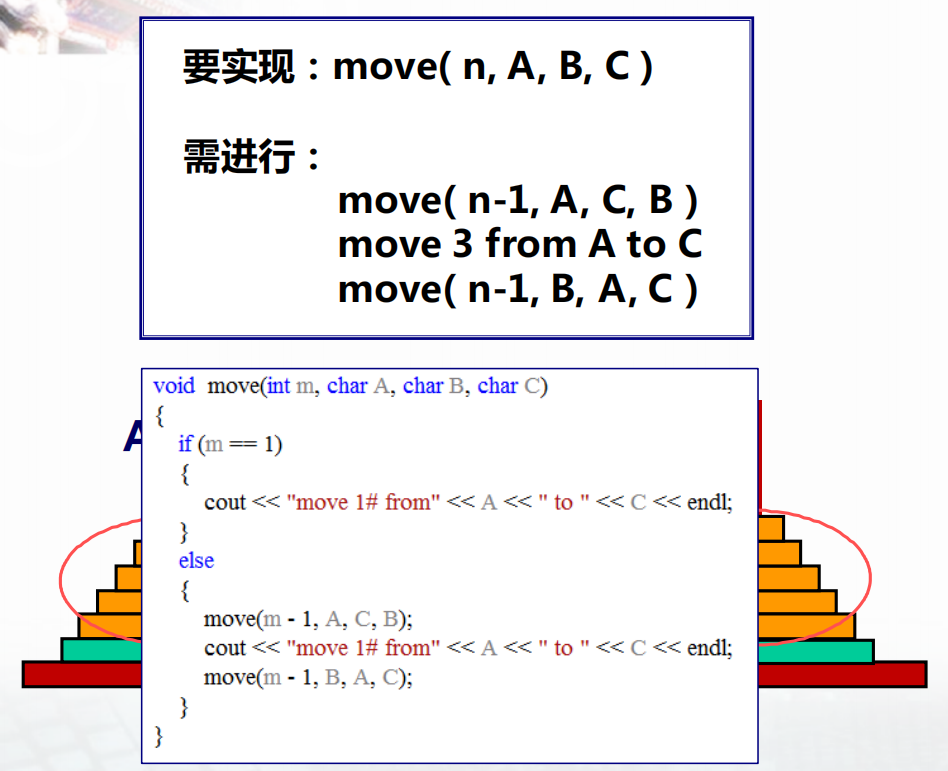
QQ图片20200201112717

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
using namespace std;
void move(int m, char A, char B, char C) //表示将m个盘子从A经过B移动到C
{
	if (m == 1)
	{
		cout << "move 1# from" << A << "to" << C << endl;  //直接可解结点
	}
	else  //如果m不为1，则要调用move(m-1)
	{
		move(m - 1, A, C, B);
		cout << "move 1# from" << A << "to" << C << endl;
		move(m - 1, B, A, C);
	}
}
int main()
{
	int n;
	cout << "请输入盘数n=" << endl;
	cin >> n;
	cout << "在3根柱子上移" << n << "个盘子的步骤为：" << endl;
	move(n, 'A', 'B', 'C');
	return 0;
}

QQ图片20200201112602

进行“自动的分析”

先假设有一个函数能给出答案，再利用这个函数分析如何解决问题；搞清楚最简单的情况下答案是什么。

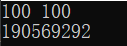
例子：放苹果

把m个同样的苹果放在n个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？注意：5,1,1和1,5,1是同一种分法。

思路：

  1. 假设有一个函数f(m,n)能解决这个问题，那么最简单的情况是m<=1||n<=1，此时只有1种分法。

  2. 当n>m时，必有盘子会空着，空着的盘子不影响结果，那么有f(m,n)=f(m,m)。

  3. 当n<=m时，分两种情况：

    (1)如果有盘子空着，那么减少一个盘子也不会影响结果，有f(m,n)=f(m,n-1)。

    (2)如果盘子全满，那么每个盘子至少有1个苹果，那么只需考虑剩下m-n个苹果在n个盘子中的分法，则有

    f(m,n)=f(m-n,n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include<iostream>
using namespace std;
int count(int m, int n)
{
	if (m <= 1 || n <= 1)   return 1;
	if (m < n)
		return count(m, m);
	else
		return count(m, n - 1) + count(m - n, n);
}
int main()
{
	int m, n;
	cin >> m >> n;
	cout << count(m, n) << endl;
}

QQ图片20200201114810

递归问题解法小结

面对一个问题时：

  1. 假设有一个函数f()可以解决问题；接下来考虑这个函数是什么样的？
  2. 找到f^n()与f^n-1()之间的关系；
  3. 确定f()的参数；
  4. 分析并写出边界条件。

例子1：组合问题

用递归法计算从n个人中选择k个人组成一个委员会，求不同的组合的个数一共是多少？

思路：

  • 由n个人里选k个人的组合数=由n-1个人里选k个人的组合数+由n-1个人里选k-1个人的组合数；
  • 当n = k或k = 0时，组合数为1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<iostream>
using namespace std;
int comm(int n, int k)
{
	if (k > n)
		return 0;
	else if (n == k || k == 0)
		return 1;
	else
		return comm(n - 1, k) + comm(n - 1, k - 1);
}

int main() 
{
	int n, k;
	cout << "Please enter two integers n and k: ";
	cin >> n >> k;
	cout << "C(n,k) = " << comm(n, k) << endl;
	return 0;

}

QQ图片20200202104441

探索式递归

例子1：下楼问题

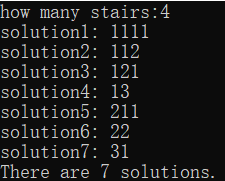
从楼上走到楼下共有h个台阶，每一步有3种走法：走1个台阶；走2个台阶；走3个台阶。问可以走出多少种方案？将所有的方案输出。

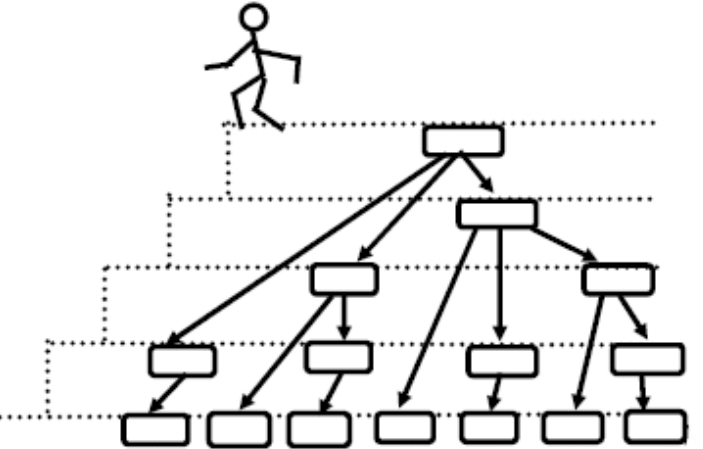
QQ图片20200201183838

思路：

  1. 既然要列出所有方案，所以需要用一个数组存放每步走的步数，可设为take[99]，步数存放在take[ ]中，满足条件就打印出来；

  2. 假设有一个函数Try( )能解决问题，接着寻找Try^n^( )与Try^n+1^( )的关系；

  3. Try^n^( )代表走完第n步的状态，即已经填完第n个take[ ]；

  4. Try^n( )与Try^n+1( )的关系：在走完第n步后，再走第n+1步时，有三种选择（走1、2、3步），每个选择下有三种可能性：

    • 如果剩下的台阶数小于想要走的步数：返回
    • 如果剩下的台阶数恰好等于要走的步数：打印输出
    • 如果剩下的台阶数大于想要走的步数：走下去
  5. Try( )的参数如何确定：Try^n^( )与Try^n+1^( )之间哪些数据是不一样的？而且是需要由Try^n( )传递给Try^n+1^( )的？

​ Try^n^( )代表走完第n步的情况，Try^n+1^( )代表走完第n+1步的情况；

​ Try^n^( )需要将走完第 n步后剩余的台阶数传递 给Try^n+1^( )。

​ 因此可以将Try^n^( )定义为：Try(i, s)，i表示剩余的台阶数，s表示步数。

QQ图片20200201185823

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<iostream>
using namespace std;
int take[99];    //记录每一个走的台阶数
int num = 0;     //num记录解决方案的个数
void Try(int i,int s)
{
	for (int j = 1; j <= 3; j++)
	{
		if (i < j)
			continue;
		take[s] = j;
		if (i == j)
		{
			num++;
			cout << "solution" << num << ": ";
			for (int k = 1; k <= s; k++)
				cout << take[k];
			cout << endl;
		}
		else
			Try(i - j, s + 1);
        //take[s]=0;  
	}
}
int main()
{
	int h = 0;
	cout << "how many stairs:";
	cin >> h;
	Try(h, 1);
	cout << "There are " << num << " solutions." << endl;
	return 0;
}

QQ图片20200201191406

例子2：字母全排列

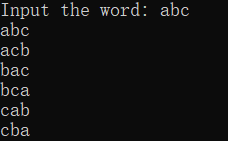
从键盘读入一个英文单词（全部字母小写，且该单词中各个字母均不相同），输出该单词英文字母的所有全排列。

如输入abc，则打印出abc, acb, bac, bca, cab, cba。

思路：

需要反复做的事情是：选择第n个位置的字母，依次检查每个字母，如果某个字母没被选择过，则进行：

  1. 将该字母放第n个位置；
  2. 标记该字母已经被选择；
  3. 如果全部位置都已选完，打印输出；否则，为下一个位置选择字母；
  4. 把刚刚标记过的字母重新标记为“未选择”；

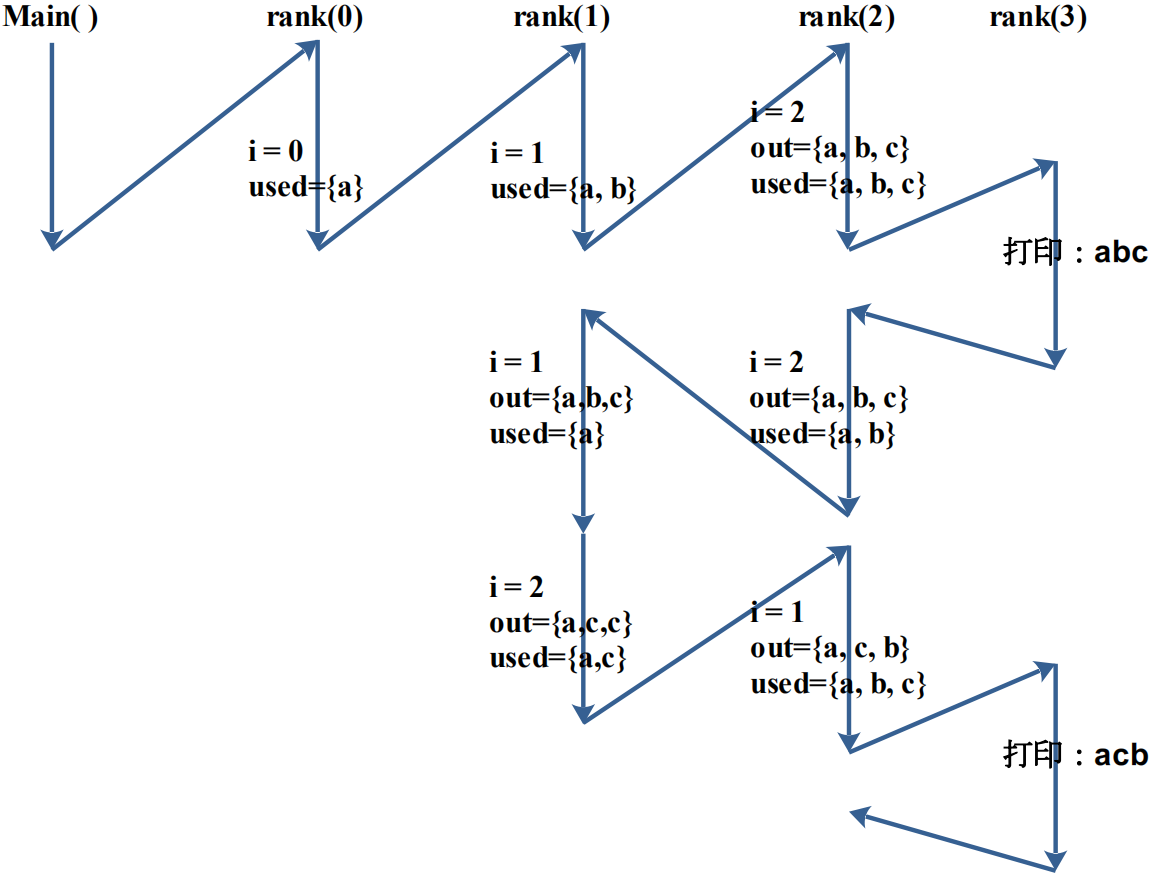
假设一个函数ranker( )能够完成上述事情，每次调用之间的区别在于位置n，ranker(1)—>ranker(2)—>ranker(3)……—>ranker(n)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
using namespace std;
char in[30] = { 0 };    //存放输入的单词
char out[30] = { 0 };   //存放准备输出的字符串
int used[30] = { 0 };   //记录第i个字母是否已经使用过
int length = 0;         //记录输入的单词的长度

void ranker(int n)
{
	if(n==length)       //如果全部字母已经被选择完，则打印输出
	{
		cout << out << endl;
		return;
	}
	for (int i = 0; i < length; i++)  //依次查看每个字母
	{
		if (!used[i])          //如果某个字母没有被选用
		{
			out[n] = in[i];    //选入该字母
			used[i] = 1;       //标记该字母已经被选择
			ranker(n + 1);     //为下一个位置寻找字母
			used[i] = 0;	   //回溯，标记字母未被使用，让其可重新被选择
		}
	}
}

int main()
{
	cout << "Input the word: ";
	cin >> in;
	length = strlen(in);
	ranker(0);   //从第一个字母开始
	return 0;
}

QQ图片20200201195215

QQ图片20200201201948

例子3：分书问题

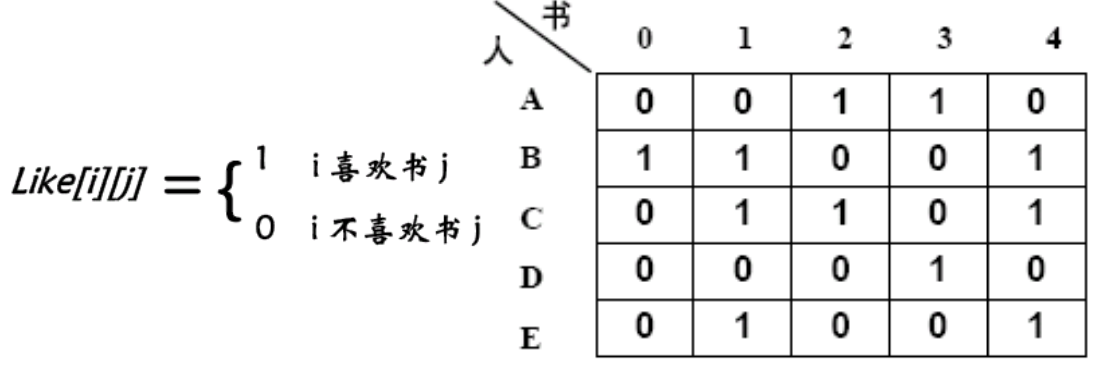
有编号分别为1, 2, 3, 4, 5的五本书，准备分给A，B，C，D，E五个人，每个人阅读兴趣用一个二维数组加以描述。请写一个程序，输出所有分书方案，让人人都能拿到喜欢的书。

QQ图片20200201202457

思路：

  1. 假设函数trybook( )可以解决问题，从第0个人开始分书，函数trybook(i)应该要完成：
  2. 试着给第i个人分书，从0号书开始试，当第i个人喜欢第j个书，且j书还没被选走时（因此要建一个数组记录书被选走的状态），那么第i个人就得到第j本书；
  3. 如果不满足上述条件，则什么也不做，返回循环条件；
  4. 若满足条件，则做三件事情：
    • 做事：将第j个书分给第i个人，同时记录j书已被选用；
    • 判断：查看是否将所有5个人所要的书分完，若分完，则输出每个人所得之书；若未分完，去寻找其他解决方案；
    • 回溯：让第i个人退回j书，恢复j书尚未被选用的状态。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
using namespace std;
int like[5][5] = { {0,0,1,1,0},{1,1,0,0,1},{0,1,1,0,1},{0,0,0,1,0},{0,1,0,0,1} };
int book[5] = { 0 }; //book[5]记录书是否被选用，选用记为1
int take[5] = { 0 }; //take[5]记录第i个人领到那本书
int num;             //num记录分书方案的个数
void trybook(int i)  //第i个人
{
	for (int j = 0; j <=4; j++)  //第j本书
	{
		if ((like[i][j] > 0) && (book[j] == 0)) //若第i个人喜欢第j本书，且第j本书还没被选用
		{
			take[i] = j;  //把第j本书分给第i个人
			book[j] = 1;  //记录第j本书已经被选用
			if (i == 4)   //如果第5个人已经拿到书，即书已分完，则输出方案
			{
				num++;
				cout << "第" << num << "个方案" << endl;
				for (int k = 0; k <= 4; k++)
					cout << take[k] << "号书给" << char(k + 65)<<" ";
				cout << endl;
			}
			else       //如果书没分完，则继续给下一个人分书
				trybook(i + 1);
            //take[i] = -1;  把第i个人的书退回，实际上可以不加这一条
			book[j] = 0;   //回溯，把第j本书标记为未选用
		}
	}
}

int main()
{
	int n = 0;
	trybook(0);
	return 0;
}

QQ图片20200202101401

探索式递归问题的解法

第n步需要做什么？对于面前的每种选择：

  1. 把该做的事情做了；
  2. 判定是否得到解；
  3. 递归（调用第n+1步）；
  4. 看是否需要回溯。