计算
对象:规律,技巧
目标:高效,低耗
Computer science should be called called computing science, for the same reason why surgery is not called knife science.
-E.Dijkstra
- 计算 = 信息处理
借助某种工具,遵照一定规则,以明确而机械的形式进行
- 计算模型 = 计算机 = 信息处理工具
算法
所谓算法,即特定计算模型下,旨在解决特定问题的指令序列
输入:待处理的信息(问题)
输出:待处理的信息(答案)
正确性:的确可以解决指定的问题
确定性:任一算法都可以描述为一个由基本操作组成的序列
可行性:每一基本操作都可以实现,且在常数时间内完成
有穷性:任一算法在执行有限次基本操作之后终止并给出输出
- 列子:Hailstone序列
1 | int hailstone(int n){//计算序列Hailstone(n)的长度 |
问题:对于任意的n,总有|Hailstone(n)| < ∞ ?
目前还不能证明
- 程序不一定是算法
好算法
正确:符合语法,能够编译,链接
能够正确处理简单的,大规模的,一般性的,退化的,任意合法的输入
健壮:能辨别不合法的输入并做适当处理,而不致非正常退出
可读性:结构化 + 准确命名 + 注释 + …
效率:速度尽可能快 ;存储空间尽可能少 (最重要的)
Algorithms + Data Structures = Programs -N. Wirth, 1976
(Algorithms + Data Structures) × Efficiency = Computation
计算模型
好的数据结构和算法才能有高效的计算,从而有好的应用。
算法分析
两个主要方面:
正确性:算法功能与问题要求一致?
数学证明?并不简单
成本: 运行时间+所需存储空间
如何度量?如何比较?
考察:$T_A(P)$ = 算法A求解问题实例P的计算成本。
意义不大,因为可能出现的问题实例太多。那么如何归纳概括?
观察:问题实例的规模,往往是决定计算成本的主要因素。
特定算法 + 不同实例
- 令$T_A(n)$ = 用算法A求解某一问题规模为n的实例,所需的计算成本。
讨论特定算法A(及其对应的问题)时,简记作$T(n)$。
然而这一定义仍有问题,同一问题等规模的不同实例,计算成本不尽相同,甚至有实质差别。
稳妥起见,取$T(n) = max\{ T(P)| |P| = n \}$,亦即,在规模同为n 的所有实例中,只关注最坏(成本最高)的实例。
特定问题 + 不同算法
- 同一问题通常有多种算法,如何评判其优劣?
- 实验统计是最直接的方法,但足以准确反映算法的真正效率?
- 但实验统计还是不足够的,还要考虑:
- 不同的算法,可能更适应于不同规模的输入
- 不同的算法,可能更适应 与不同类型的输入
- 同一算法,可能由不同程序员、用不同程序语言、经不同编译器实现
- 同一算法,可能实现并运行与不同的体系结构、操作系统
- 为给出客观的评判,需要抽象出一个理想的平台或模型
- 不再依赖于上述种种具体的因素
- 从而直接而准确地描述,测量并评价算法
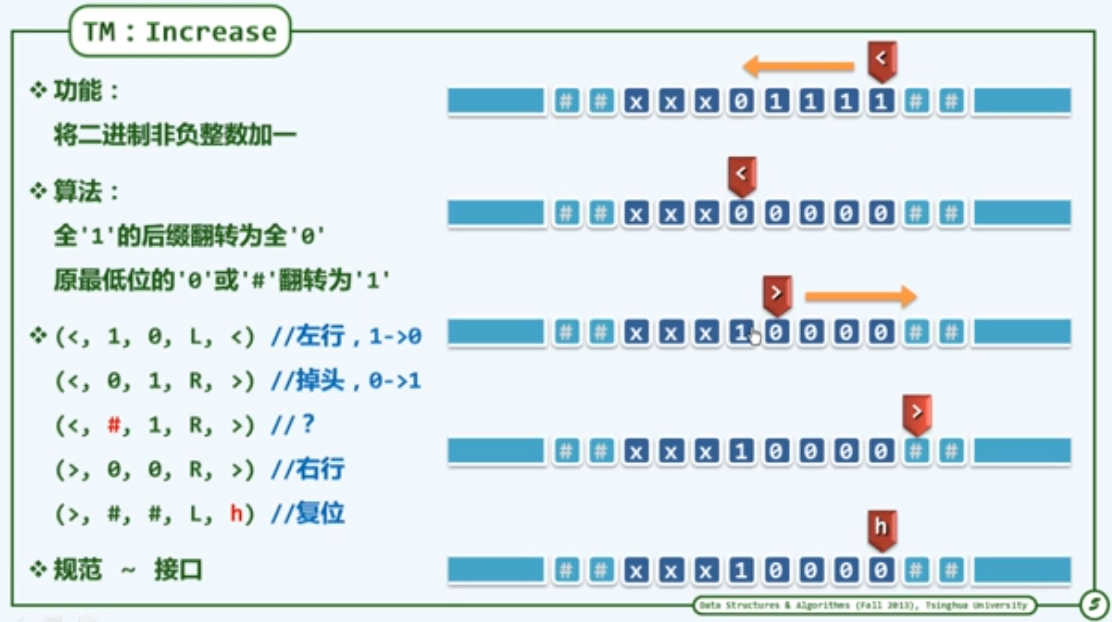
图灵机 Turing Machine
- Tape:依次均匀地划分为单元格,各注有某一字符,默认为’#’
- Alphabet:字符的种类有限
- Head:总是对准某一单元格,并可读取和改写其中的字符;每经过一个节拍,可转向左侧或右侧的邻格
- State:TM总是处于有限种状态中的某一种,每经过一个节拍,可(按照规则)转向另一种状态
- Transition Function :(q, c; d, L/R, P)
若当前状态为q且当前字符为c,则将当前字符改写为d;转向左侧/右侧的邻格;
转入p状态,一旦转入特定的状 态’h’,则停机。
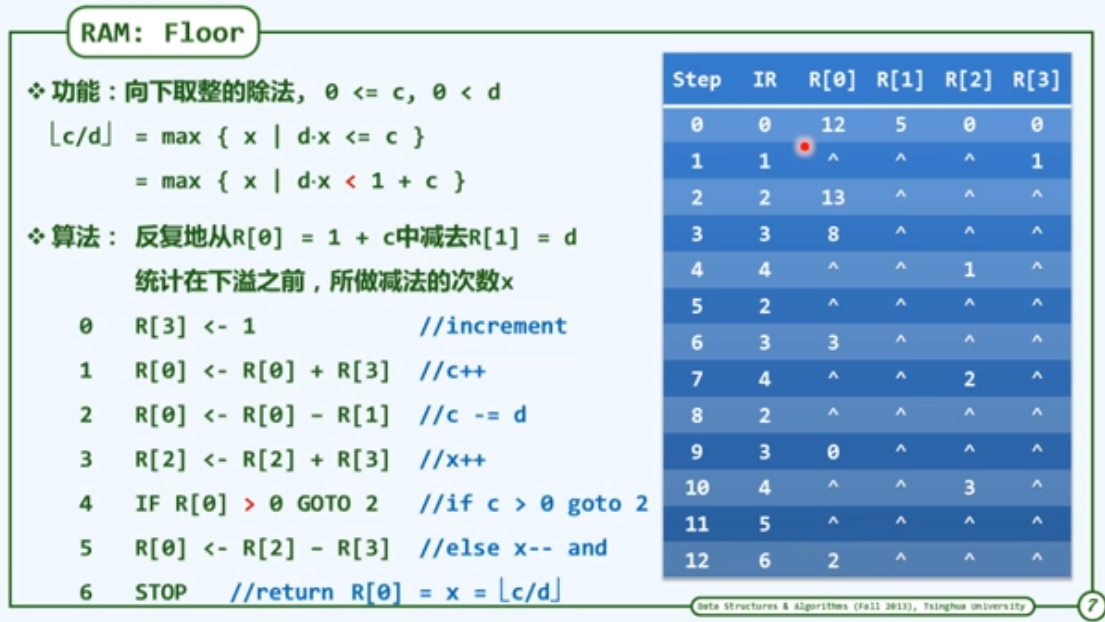
RAM: Random Access Machine
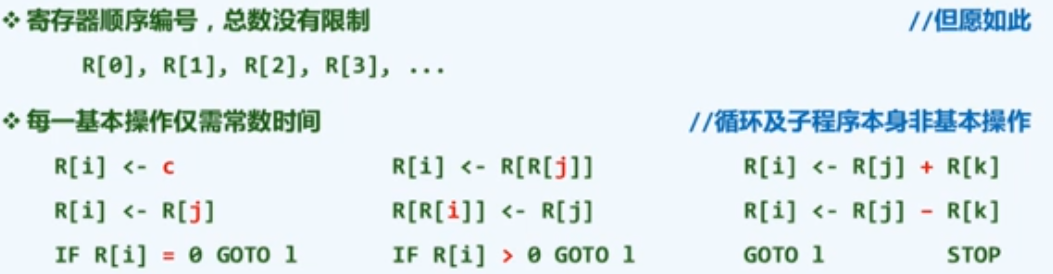
与TM模型一样,RAM模型也是一般计算工具的简化与抽象,使我们可以独立于具体的平台,对算法的效率做出可信的比较与评判。
在这些模型中:
- 算法的运行时间 转化为 算法需要执行的基本操作次数
- $T(n)$ = 算法为求解规模为n的问题,所需执行的基本操作次数
大$O$记号
渐进分析
- 回到原先的问题:随着问题规模的增长,计算成本如何增长?
注意:这里更关心足够大的问题,注重考察成本的增长趋势
- 渐进分析:在问题规模足够大后,计算成本如何增长?
Asymptotic analysis:当n>>2后,对于规模为n输入,算法
需执行的基本操作次数:T(n) = ?
需占用的存储单元数:S(n) = ? //通常可不考虑
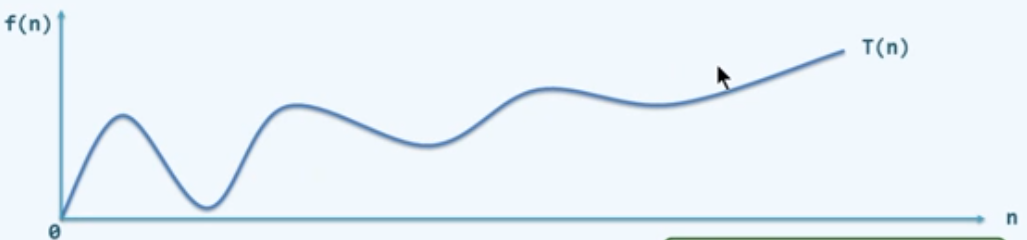
大$O$记号(big-$O$ notation)
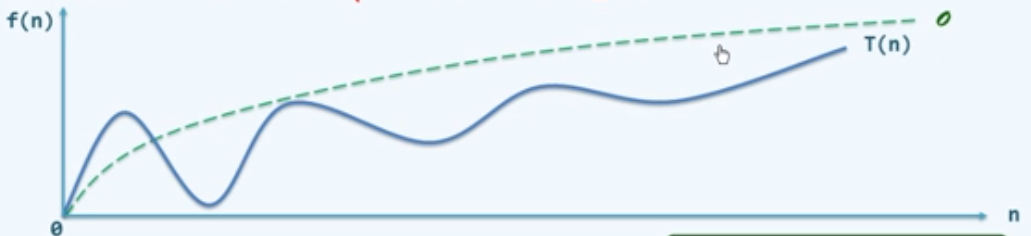
与T(n)相比,f(n)更为简洁,但依然反映前者的增长趋势
- 常系数可忽略:$O(\,f(n)\,)=O(c\times \,f(n)\,)$
- 低次数可忽略:$O(n^a+n^b)=O(n^2),\,a>b>0$
其它记号:
- $T(n)=\Omega(\,f(n)\,)$:
$ \exists c>0, 当n>>2后,有T(n)<c\cdot f(n)$
- $T(n)=\Theta(\,f(n)\,)$:
$ \exists c_1>c_2>0, 当n>>2后,有c_1\cdot f(n)>T(n)>c_2\cdot f(n)$

刻度
下面讨论大$O$记号的几种”刻度“:
$O(1)$
常数(constant function)
$2=2013=2013\times 2013=O(1)$,甚至$2013^2013=O(1)$
这类算法的效率最高
什么样的代码对应于常数执行时间?
一般地,不含循环;不含分支转向;不能有(递归)调用,应具体问题具体分析
$O(log^c n)$
- 对数$O(log^c n)$
- 常底数无所谓
$\forall a,b>0,\,log_an=log_ab\cdot log_bn=\Theta(logn)$
- 常数次幂无所谓
$\forall c>0,\,logn^c=c\cdot logn=\Theta(logn)$
对数多项式(ploy-log function)
$123\cdot log^{321}n+log^{105}(n^2-n+1)=\Theta(log^{321}n)$
这类算法非常有效,复杂度无限接近于常数
$\forall c>0,\,logn=\Theta(n^c)$
$O(n^c)$
多项式(polynomial function)
$(100n-500)(20n^2-300n+2013)=O(n\times n^2)=O(n^3)$
一般地,$a_kh^k+a_{k-1}n^{k-1}+\dots+a_1n+a_0=O(n^k),\,a_k>0$
线性(linear function):所有$O(n)$函数
这门课主要覆盖的范围:从$O(n)$到$O(n^2)$
这类算法的效率通常认为已可令人满意
$O(2^n)$
- 指数(exponential function):$T(n)=a^n$
- $\forall c>1,\,n^c=O(2^n);\,n^{1000}=O(1.00001^n)=O(2^n);\,1.00001^n=\Omega(n^{1000})$
- 这类算法的计算成本增长极快,通常被认为不可忍受
- 从$O(n^c)$到$O(2^n)$,是从有效算法到无效算法的分水岭
- 很多问题的$O(2^n)$算法往往显而易见,然而设计出$O(n^c)$算法却极为不易,甚至有时注定只能是徒劳无功。
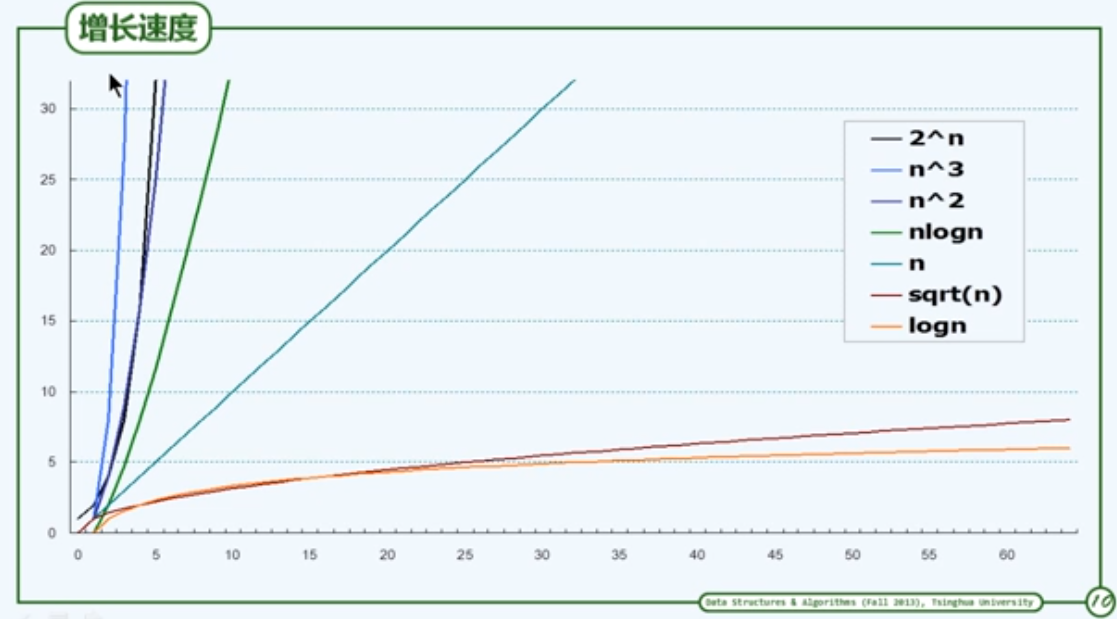
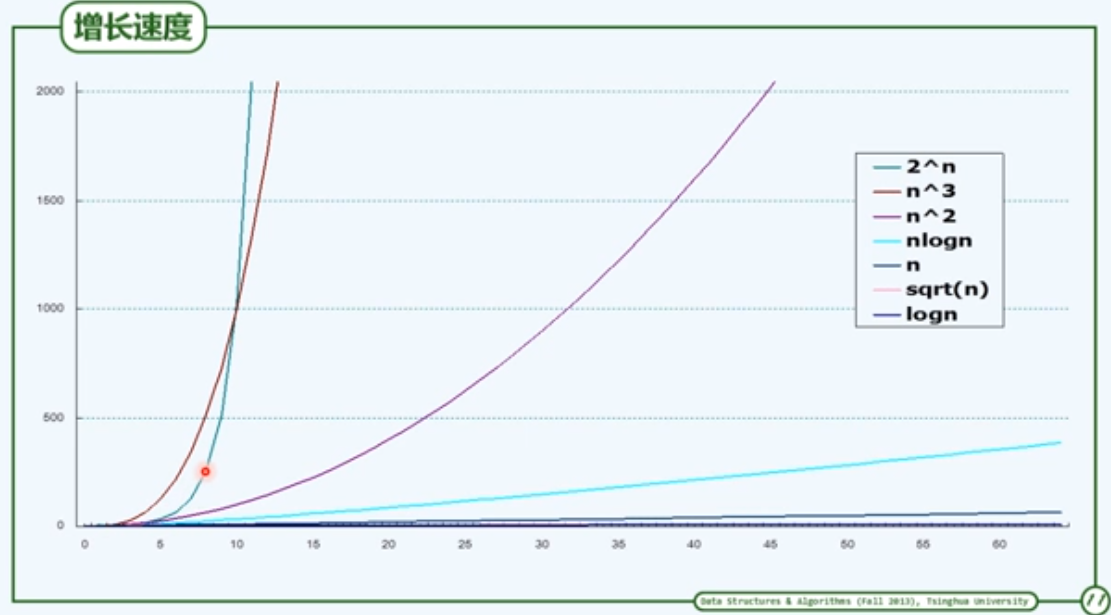
例子:2-Subset
S包含n个正整数,$\sum S=2m$,S是否有子集T,满足$\sum T=m$?
- 直觉算法:逐一枚举S的每一个子集,并统计其元素的总和
- 定理:$|2^s|=2^{|s|}=2^n$,亦即直觉算法需要迭代$2^n$轮,并(在最坏情况下)至少需要花费这么多时的间
- 但实际上上述的直觉算法已属最优解,就目前的计算模型而言,不存在可在多项式时间内回答此问题的算法。
- 2-Subset is NP-complete
算法分析
两个主要任务 = 正确性(不变形 × 单调性) + 复杂度
那么为了确定复杂度,真地需要将算法描述为RAM的基本指令,再统计累计的执行次数嘛?答案是不必的。
C++等高级语言的基本指令,均等效于常数条RAM的基本指令;在渐进意义下,二者大体相当:
- 分支转向:goto //算法的灵魂,出于结构化考虑,被隐藏了
- 迭代循环:for( )、while( )…… //本质上就是 if + goto
- 调用 + 递归(自我调用) //本质上也是goto
复杂度分析的主要方法:
- 迭代:级数求和
- 递归:递归跟踪 + 递推方程
- 猜测 + 验证
级数
- 算数级数:与末项平方同阶
$T(n)=1+2+\dots +n=n(n+1)/2=O(n^2)$
- 幂方级数:比幂次高出一阶
$\sum_{k=0}^nk^d\approx \int_0^n x^{d+1}dx=\frac{1}{d+1}x^{d+1}\mid_0^n=\frac{1}{d+1}n^{d+1}=O(n^{d+1})$
$T_2(n)=1^2+2^2+3^2+\dots+n^2=n(n+1)(2n+1)/6=O(n^3)$
$T_3(n)=1^3+2^3+3^3+\dots+n^3=n^2(n+1)^2/4=O(n^4)$
- 几何级数(a>1):与末项同阶
$T_a(n)=a^0+a^1+\dots+a^n=(a^{n+1}-1)/(a-1)=O(a^n)$
$1+2+4+\dots+2^n=2^{n+1}-1=O(2^{n+1})=O(2^n)$
- 收敛级数
$1/2/2+1/2/3+1/3/4+\dots+1/(n-1)/n=1-1/n=O(1)$
$1+1/2^2+\dots+1/n^2<1+1/2^2+\dots=\pi^2/6=O(1)$
$1/3+1/7+1/8+1/15+/24+1/26+1/31+1/35+\dots=1=O(1)$
实际上讨论这类分数级数是有必要的,因为在某种意义上,基本操作次数,存储单元数可以看作是分数,例如将某个循环条件执行的概率设为$\lambda$,则其数学期望为:
$(1-\lambda)\cdot[1+2\lambda+3\lambda^2+4\lambda^3+\dots]=1/(1-\lambda)=O(1),0<\lambda<1$
- 某些不收敛但长度有限的级数
$h(n)=1+1/2+1/3+\dots+1/n=\Theta(logn)$ 调和级数
$log1+log2+log3+\dots+logn=log(n!)=\Theta(nlogn)$ 对数级数
循环与级数
1 | for(int i=0; i<n; i++) |
算术级数:$\sum_{i=0}^{n-1}=n+n+\dots+n=n\cdot n=O(n^2)$
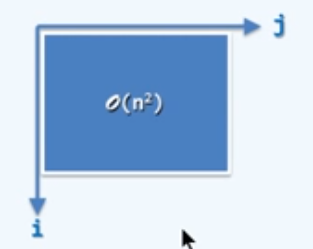
1 | for(int i=0; i<n; i++) |
算术级数:$\sum_{i=0}^{n-1}=0+1+\dots+(n-1)=\frac{n(n-1)}{2}=O(n^2)$
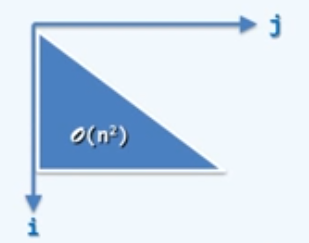
1 | for(int i=0; i<n; i++) |
算术级数:$O(n^2)$
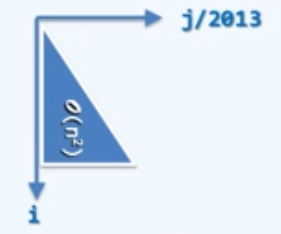
1 | for(int i=0; i<n; i<<=1) // i<<=1 左移一位,相当于乘2 |
几何级数:$1+2+4+\dots+2^{[log_2(n-1)]}={\sum}_{k=0}^{[log_2(n-1)]}2^k=2^{[log_2(n-1)]}-1=n-1=O(n)$
取非极端元素
问题:给定整数子集S,|S| = n >=3,找出元素$a\in S,a\ne max(S),且 a\ne min(S) $
算法:从S中任取三个元素{x, y, z} //若S以数组形式给出,不妨取前三个;由于S是集合,这三个元素必互异
确定并排除其中的最小者,最大者 //不妨设 x = max{x, y, z}, y = min{x, y, z}
输出剩下的元素z
无论输入规模n多大,上述算法需要的执行时间不变
$T(n)=常数=O(1)=\Omega(1)=\Theta(1)$
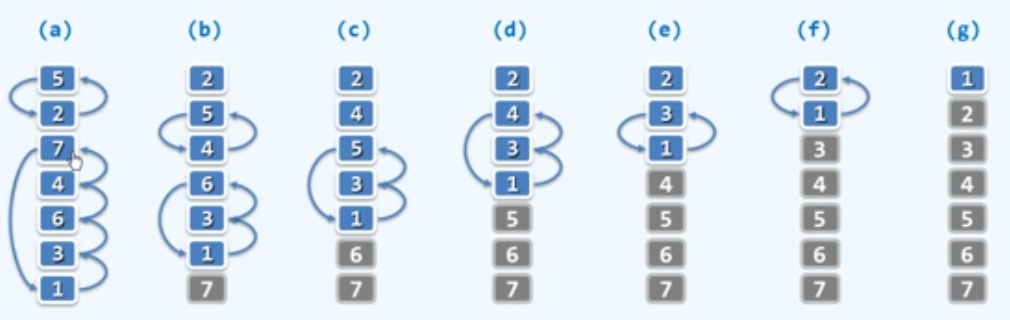
起泡排序
问题:给定n个整数,将它们按非降序排列
观察:有序/无序序列中,任意/总有一对相邻元素顺序/逆序
扫描交换:依次比较每一对相邻元素,如有必要,交换之;若整趟扫描都没有进行交换,则排序完成;否则,再做一趟交换
1 | void bubblesort(int A[], int n) |
接下来考虑算法的正确性
问题:该算法必然会结束?至多需迭代多少趟?
不变性:经k轮扫描交换后,最大的k个元素必然就位
单调性:经k轮扫描交换后,问题规模缩减至n-k
正确性:经至多n趟扫描后,算法必然终止,且能给出正确答案
通过挖掘并且综合算法的不变性和单调性,进而证明算法正确性的方法是算法分析中的一个基本且重要的方法。
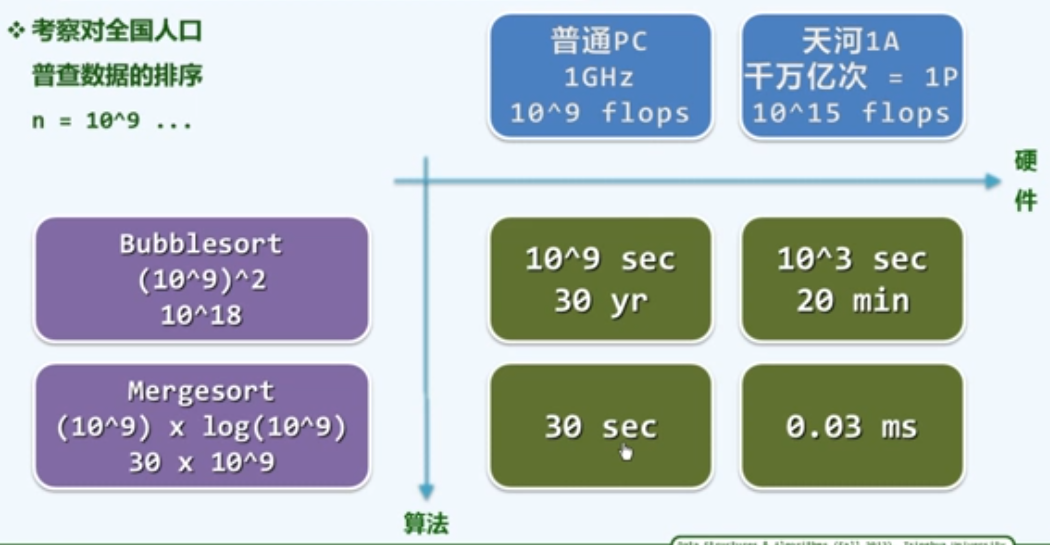
封底估算
除了大$O$记号这种定性的方法,我们在很多时候也需要定量的估算,一种常用的方法是封底估算(Back-of-the-Envelope Calculation)
迭代和递归
To iterate is human, to recurse, divine.
例子:数组求和(迭代)
问题:计算任意n个整数之和
实现:逐一取出每个元素,累加之
1 | int SumI(int A[], int n) { |
无论A[ ]内容如何,都有时间复杂度为:
$T(n)=1+n*1+1=n+2=O(n)=\Omega(n)+\Theta(n)$
如果把输入参数中的n看作是这个问题的规模,其中最重要的循环部分,每经过一次迭代,有一个数已经统计完毕,而相应的尚未参与统计的元素,即尚未解决的问题的规模就会递减一个元素,这种通过不断削减问题的有效规模的方法就是减而治之。
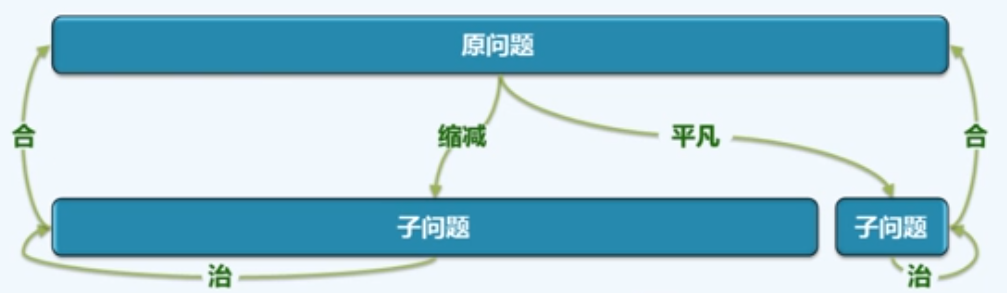
减而治之(Decrease-and-conquer)
为求解一个大规模的问题,可以将其划分为两个子问题:其一平凡易解,另一规模缩减;分别求解子问题;由子问题的解,得到原问题的解。
数组求和:线性递归
1 | sum(int A[], int n){ |
- 递归跟踪(recursion trace)分析:
检查每个递归实例;累计所需时间(调用语句本身,计入对应的子实例);其总和即算法执行时间
- 本例中,单个递归实例自身只需$O(1)$时间
$T(n)=O(1)*(n+1)=O(n)$
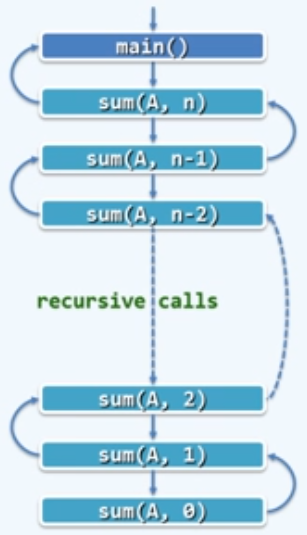
- 从递推的角度看,为求解
sum(A, n),需要
递归求解规模为n-1的问题sum(A,n-1) //T(n-1)
再累加上A[n-1] //$O(1)$
递归基:sum(A, 0) //$O(1)$
- 递推方程:$T(n)=T(n-1)+O(1)$ //recurrence
$T(0)=O(1)$ //base
- 求解: $T(n)-n=T(n-1)-(n-1)=\dots=T(2)-2=T(1)-1=T(0)$
$T(n)=O(1)+n=O(n)$
数组倒置
任给数组A[n],将其前后颠倒
1 | void reverse(int *A, int lo, int hi) |
由递推方程:$T(n)=T(n-2)+O(1)$可得其时间复杂度为:$O(n)$。

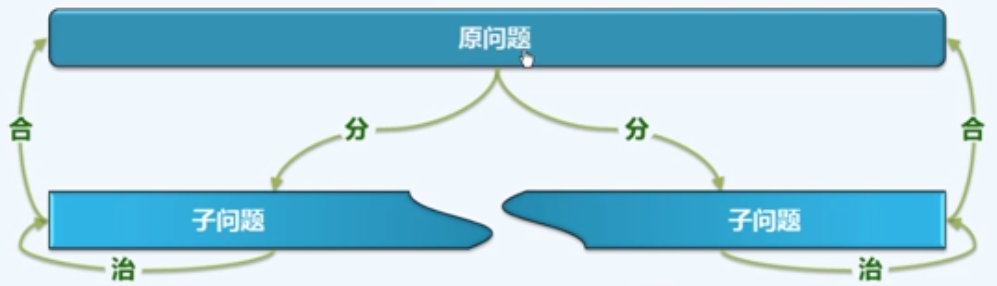
分而治之(Divide-and-conquer)
为求解一个大规模的问题,可以将其划分为若干个(通常两个)子问题,规模大体相当;分别求解子问题;由子问题的解,得到原问题的解
数组求和:二分递归
1 | int sum(int A[], int lo, int hi) |
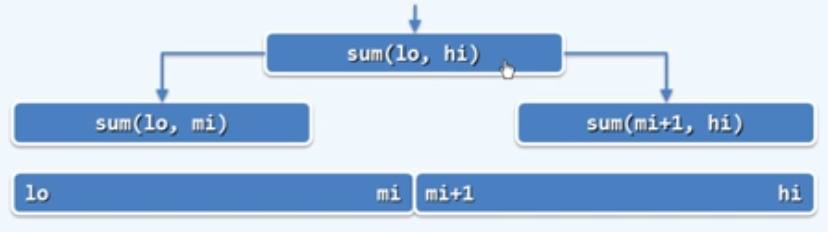
该算法的正确性毋庸置疑,接下来分析其时间复杂度:
- 从递归跟踪的角度:
$T(n)=各层递归实例所需时间之和=O(1)\times(2^0+2^1+2^2+\dots+2^{logn})=O(n)$
(几何级数的时间复杂度与末项同阶)
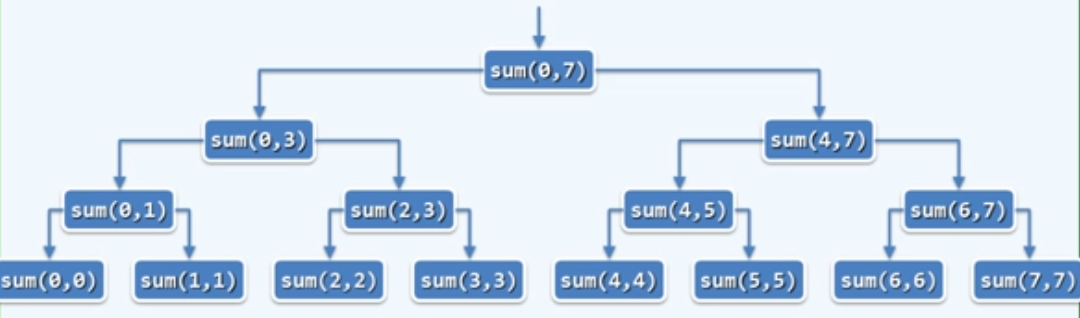
从递推的角度:为求解
sum(A, lo, hi),需要 递归求解
sum(A, lo, mi)和sum(A, mi+1, hi);进而将子问题的解累加
递归基:sum(A, lo, lo)
递推关系:$T(n)=2*T(n/2)+O(1)$
$T(1)=O(1)$
求解: $T(n)=O(n)$
Max2
从数组区间A[lo, hi)中找出最大的两个整数A[x1]和A[x2],元素比较的次数,要求尽可能地少.
迭代1

1 | void max2(int A[], int lo, int hi, int &x1, int &x2) |
无论如何,该算法的比较次数总是$\Theta(2n-3)$
迭代2
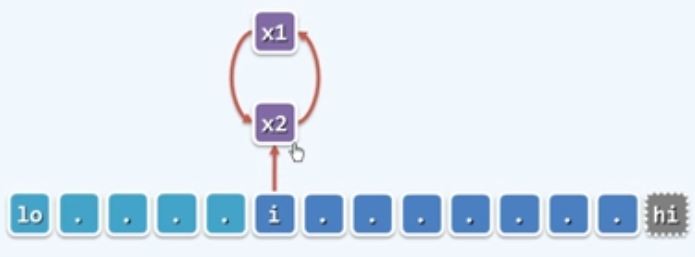
1 | void max2(int A[], int lo, int hi, int &x1, int &x2) |
最好情况:$1+(n-2)\times1=n-1$
最坏情况:$1+(n-2)\times2=2n-3$;就最坏的情况而言,这种算法并没有改进
递归+分治
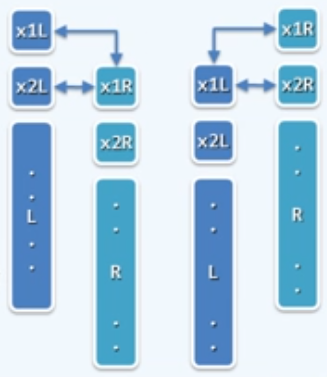
将数组二分为左侧和右侧两部分,分别找出最大值和次大值,再进行比较;每一侧又可以继续二分,实现递归。
1 | void max2(int A[], int lo, int hi, int &x1, int &x2) |
该算法的时间复杂度:$T(n)=2*T(n/2)+2\le5n/3-2$
动态规划
Make it work, make it right, make it fast.
前两步work和right可以通过递归解决,而最后一步fast可以通过迭代解决。
斐波那契数列fib( )
$fib(n) = fib(n-1) + fib(n-2) : \{0, 1, 1, 2, 3, 5, 8, ……\}$
fib( ):递归
1 | int fib(n) |
实际上当n较大时,这个递归算法的计算是很慢的,其时间复杂度为:
$T(0)=T(1)=1;\,T(n)=T(n-1)+T(n-2)+1,\,n>1$
令:$S(n)=[T(n)+1]/2$
则:$S(0)=1=fib(1),\,S(1)=1=fib(2)$
故:$S(n)=S(n-1)+S(n-2)=fib(n+1)$
$T(n)=2*S(n)-1=2\times fib(n+1)-1=O(fib(n+1))=O(\Phi^n)=O(2^n)$ ,
其中:$\Phi=\frac{1+\sqrt{5}}{2}=1.61803…$,即黄金分割数
可见该算法的时间复杂度和fib数列的n+1项的值是一个量级的。
接着对这个$O(\Phi^n)$进行较准确的估算,用封底估算的方法有:
$\Phi^{36}=2^{25},\,\Phi^{43}=2^{30}=10^9flo=1sec$
$\Phi^{5}=10,\,\Phi^{67}=10^14flo=10^5sec$
$\Phi^{92}=10^{19}flo=10^{10}sec=10^5day=3century$
可见这并不是一个好方法。
从递归跟踪的角度来分析:
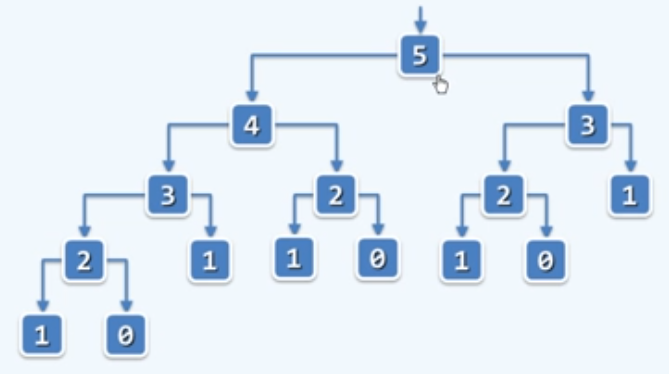
递归版fib( )低效的根源在于,各地鬼实例均被大量重复地调用
那么可以使每个实例只能调用一次嘛?答案是可以的。先后出现的递归实例,供给$O(\Phi^n)$个,而去除重复之后,总共不过$O(n)$种。
fib( ):迭代
解决方法A(记忆:memoization):
将已计算过实例的结果指标备查。
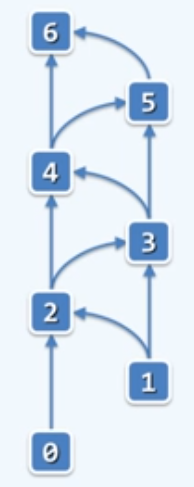
解决方法B(动态规划:dynamic programming):
颠倒计算方向,由自顶而下递归,改为自底而上迭代。不妨用两个变量f和g,分别来记忆当前我所处的相邻的两个数。
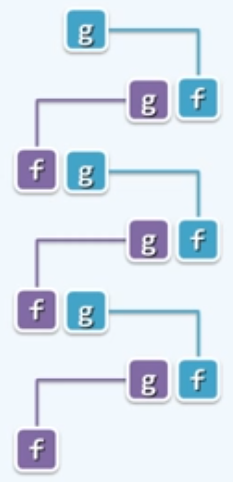
1 | int fib(n){ |
除了一个循环,没有其他增加时间复杂度的操作,而且只需要f和g两个存储单元。
$T(n)=O(n)$,而且仅需要$O(1)$空间!
最长公共子序列(LCS)
子序列(Subsequence):由序列中若干字符,按原相对次序构成(线不能有交叉)。

最长公共子序列(Longest Common Subsequence):两个序列公共子序列中的最长者。
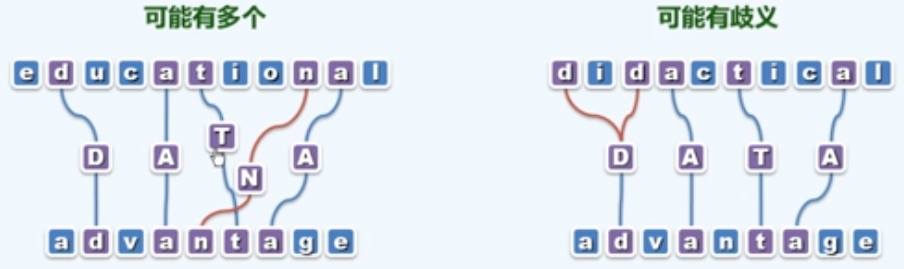
现在考虑一个较简单的问题:如何计算出任意给出的两个序列的最长公共子序列的长度?
LCS:递归
对于序列A[0, n]和B[0, m],LCS(A, B)无非三种情况
0)若n = -1 或 m = -1,则取空序列(“ ”) //递归基
1)若A[n] = ‘X’ = B[m],则取作LCS( A[0, n), B[0, m) ) + ‘X’ // 减而治之
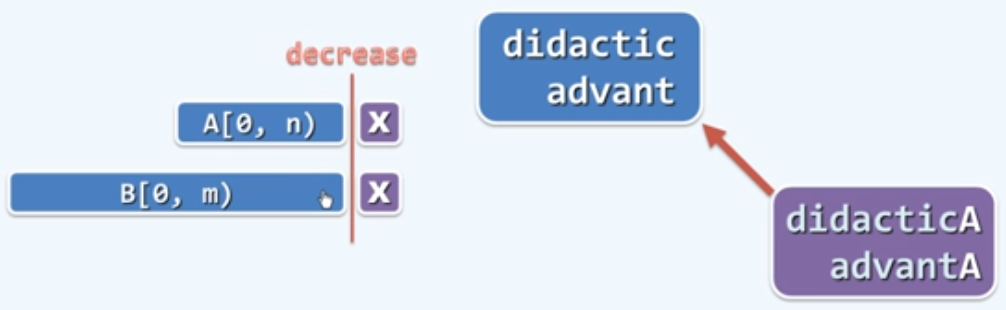
2)若A[n] $\ne$ B[m],则分别计算LCS( A[0, n], B[0, m) ),与LCS( A[0, n), B[0, m] ),取更长者。 //分而治之
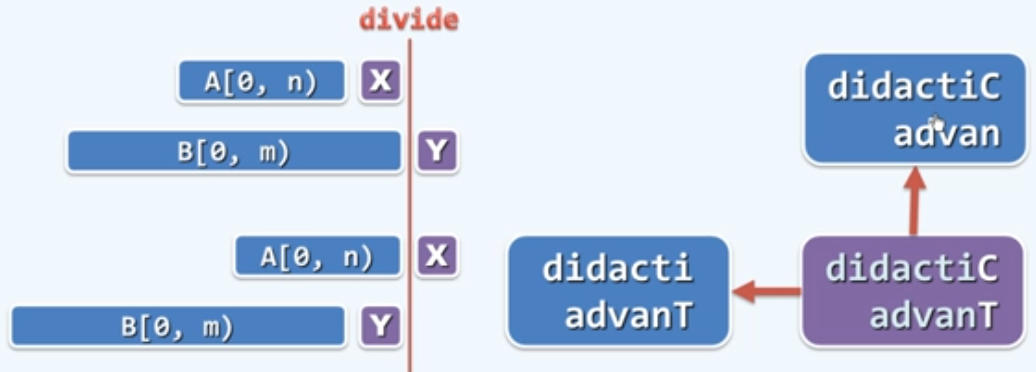
我们把上述算法中生成的所有递归实例绘制成一个表,每一个横纵坐标所确定的3×3的小方格所组成的一个大方格分别对应于一个子任务或者说是递归实例,可以看到如果是减而治之的情况,对应大方格中的一条对角线;如果是分而治之的情况,则会考虑左侧和上方的子问题,然后取更长者,保留其对应的一条边。
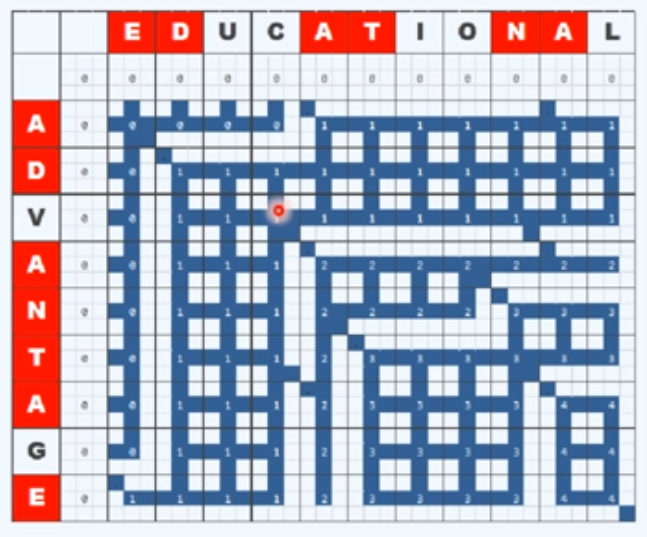
这样的形式可以帮助我们理解整个计算的过程,在这样一张表中我们最终求解的问题必然是右下角的方格对应的子问题,它分别会递归地引发一些更小的子问题,最终收缩到平凡的长度为0的子问题;我们也可以认为,每一个LCS问题的解都是从左上角(0,0)的单元开始一直沿着可行的深色的线通往右下角单元的路径,每一条路径就对应着一个解,这样就能很好地理解多解的情况。
接下来分析该算法的正确性和时间复杂度:
单调性:无论如何,每经过一次比对,原问题的规模必可减小。具体地,作为输入的两个序列,至少其一的长度缩短一个单位。
最好情况(不出现情况2))下,只需$O(n+m)$时间(线性规模)
- 但问题在于,在情况2)下原问题将分解为两个子问题,更糟糕的是,它们在随后进一步导出的子问题,可能雷同,与
fib( )的递归出现的问题类似,这种重复度往往是超出我们直观想象的。
我们将上面的图表进行局部放大:
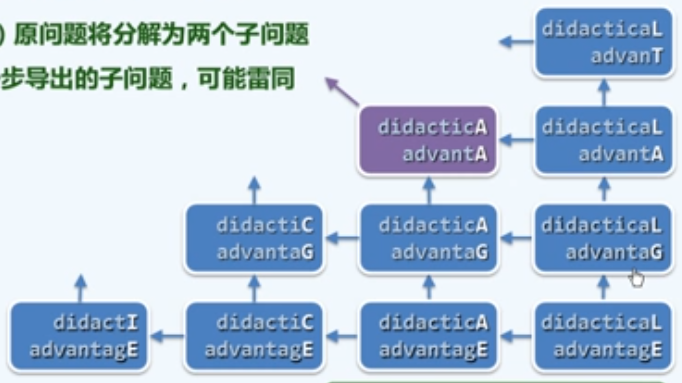
为了进行更好的估算,我们不妨从更宏观的角度来重新审视上面的表格,不妨把其中所有的递归实例分别按坐标的形式表示为(n, m),那么为了计算出最终的递归实例即(n, m)对应的解,我们需要唤醒某一个特定的递归实例(a. b)多少次呢?
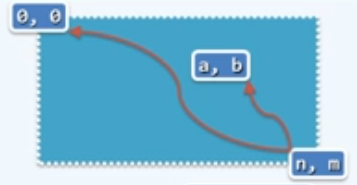
根据图表中路线行进的方向,在最坏的情况下所唤醒的次数应该等于介于这两点之间的通路的条数,每一条通路对应于(a, b)被唤醒一次,即为两点之间所有合法的通路的总长n+m-a-b中挑选出n-a条水平路径的方案数,或挑选出m-b条垂直路径的方案数。
那么在最坏情况下,LCS( A[0, a], B[0, b] )出现的次数为:
特别地,LCS( A[0], B[0] )出现的次数多达:
当$n=m$时,该算法的时间复杂度为:$O(2^n)$。
LCS:迭代
与
fib( )类似,这里也有大量重复的递归实例(子问题),(最坏情况下)先后共计出现$O(2^n)$个各子问题,分别对应于A和B的某个前缀组合,因此总共不过$O(n*m)$种
采用动态规划的策略,只需$O(n*m)$时间即可计算出所有子问题
为此,我们只需将所有子问题列成一张表,颠倒计算方向,从LCS( A[0], B[0] )出发,依次计算出所有项。
填表的规则是:首先初始化,行列都设为0,若遇到减而治之,即字母相同,则对应位置元素为其左上对角线元素+1;若遇到分而治之,即字母不相同,则对应位置元素取其上方和左侧元素中的最大值。
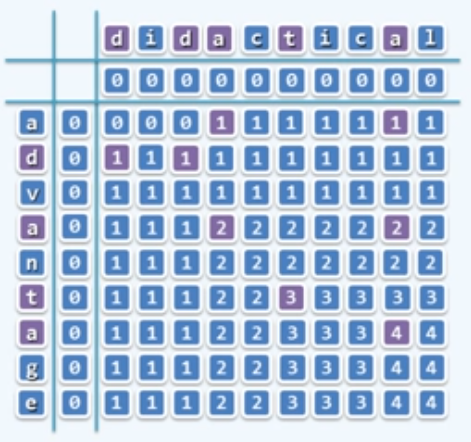
这样对于每一个子问题,只会出现一次,因此算法的时间复杂度为$O(n*m)$。