数据结构与算法（6）选择排序与插入排序

1.选择排序

与向量那一章的做法一样列表这一章的接下来几节，也将针对列表这种结构的特点介绍几种典型的排序算法，这一节要介绍的是选择排序。

1.1.构思

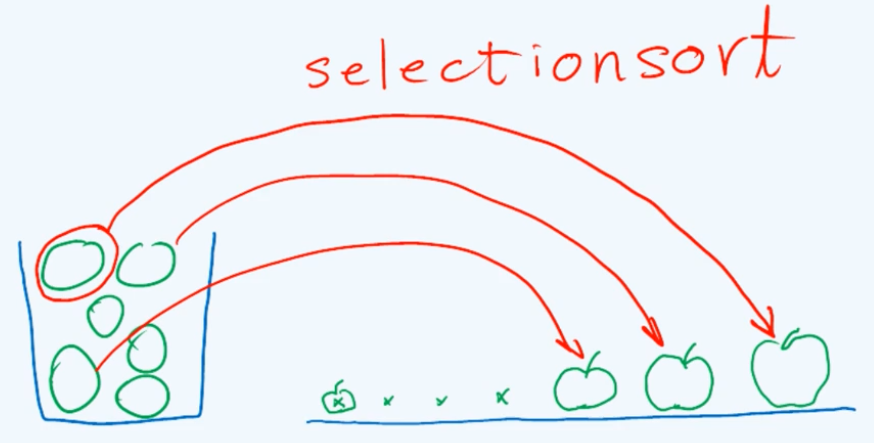
选择排序在生活中其实很常见，举个例子，假设有一篮子苹果或大或小，如果你需要从小到大把它们排成一个序列，那你会怎么做呢？常用的一种方法应该是这样的：首先在其中挑选出最大的，接下来在剩下的中挑选出最大的，即整体中次大的，如此反复，直到篮子中只剩下最后那只苹果。

可以看出在这个过程中我们所采用的策略，原则非常的简单，就是每一次只需在篮子中找出当前最大的那只苹果，并且随即将它转移到桌子上。这里每一步所做的实质的关键动作就是所谓的选择select，而基于这样一种选择过程和策略的排序算法就叫作选择排序（selection sort）。

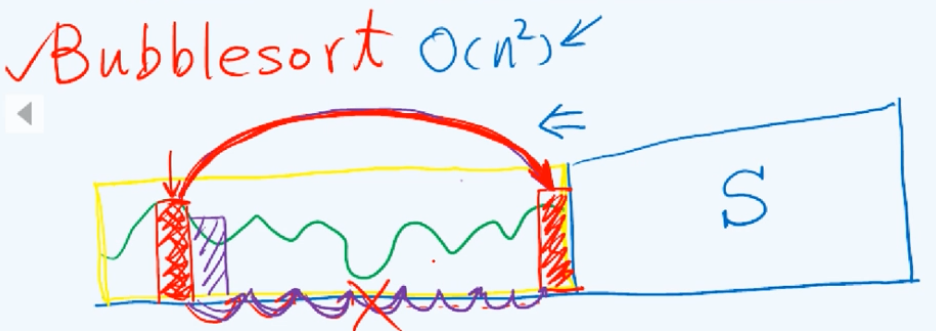
回顾一下此前所介绍过的起泡排序bubble sort，其实它也是selection sort。在起泡算法的过程中它的不变性可以表述为整个序列总是可以分成前后两个部分，其中后面的一个部分是由一系列已经就位的元素组成的，它们构成了一个有序的sorted的部分；而前半部分的元素数值的分布是随机的或大或小，但是就数值而言它们都绝对不会超过图中的黄线。这个算法是由一趟又一趟的扫描交换构成的，在接下来的一趟扫描交换中最实质的操作实际上是当前最大的那个元素和其后的元素不断地交换，直到它最终被移送到黄色区域的末尾。于是这个有序的S部分就可以向左侧拓展，这也就是起泡排序算法的单调性。

纵观这个过程并且与上面的选择排序做一对比，我们会发现二者之间的相似之处：也就是每一次扫描交换的作用其实实质上都等价于找到这个最大节点，并且随即将它转移至有序和无序子序列的分界点。从这个角度来看
起泡排序确实就是一个不折不扣的选择排序。

那反过来既然如此还有什么必要去专门讨论选择排序呢？原因在于起泡排序的效率太低，在最坏情况下它需要$O(n^2)$的时间，而借助列表结构这个效率是完全可以改进的。在起泡排序的过程中所执行的计算无非两类，一类就是相邻元素的比较，另一类才是元素位置的交换。然而很遗憾在这里将最大元素转移至合适的位置这样一个任务，是由一系列的短距离实际上是相邻元素之间的移动构成的，这种“小步慢跑式”的移动正是低效率的来源。

所以既然我们最终无非就是要将这个最大的元素挪到最终的位置，为何不直接一次性地来完成这项工作呢？这正是我们改进的思路。

1.2.实现

选择排序selection sort可以实现为下面一段代码：

//列表的选择排序算法：对起始于位置p的n个元素排序，valid(p) && rank(p) + n <= size
template < typename T> void List<T>::selectionSort(Posi(T) p, int n) { 
	 Posi(T) head = p->pred; ePosi(T) tail = p;  //待排序区间为(head, tail)
	for (int i = 0; i < n; i++) tail = tail->succ;  //head/tail可能是头/尾哨兵
	while (1 < n) { //反复从（非平凡的）待排序区间内找出最大者，并将其移至无序区间末尾
       insertBefore(tail, remove(selectMax(head->succ, n))); 
       tail = tail->pred; n--;   //待排序区间、有序区间的范围、均同步更新
	}
}

注意一下这个接口的语义，待排序的元素实际上是在列表中起始于位置p的连续n个元素，在下面的图示中，如果L是整个的列表那么待排序的区间，从节点p开始第n个节点是用虚线表示的，言下之意这里依然采用了此前左闭右开的区间定义习惯。相应地 这里引入了两个界桩head和tail。

经过入口处预处理的两步，head和tail分别对应的位置就是在这个图中的h以及p+n，在接下来的循环中 head始终不变，而tail会每次向前移动一个节点。而从tail开始到最初的界桩之间的范围正是已经排序的区间，而尚未排序的的前缀U是从p一直到T左闭右开的区间，这也是这个算法的不变性。

从算法可以看出每次我们都调用selectMax的接口，从前缀U这个区间中找到当前的最大者，n会随着迭代地进行相应地下降，从记录前缀U的宽度。在这个图中被选取出来的最大节点以M来表示，我们将M节点摘出来
插入至S区间的首节点，tail的前端，相当于将M移动到此前的T的紧邻左侧，并且随即将T移动到新的这个节点处（M处），从而使有序的部分向左拓展一个单元。这个算法将持续地迭代下去，直到n最终缩减到平凡的情况，从而完成整个指定区域的排序。

1.3.推敲

现在来重新审视一下这个算法并且对其中的几个细节来做一推敲，第一个问题是算法中套用了此前所实现的remove和insert这两个标准的操作接口，使整个代码实现更加简洁，但从效率而言还是值得推敲的。这其中的原因在于，这两个操作都要使用到动态空间分配，也就是insert的时候必须要用new，remove的时候需要delete。

虽然这两个操作都可以大致认为依然是常数的时间复杂度，但是从实际的时间消耗而言它大致是通常的基本操作的一百倍，也就是说要高出两个数量级，因此在实际中这一对操作应该尽可能少的使用。就这个意义而言，或许应该改用另外一种实现方式，比如可以只通过对M处和T处局部引用的修改，来实现同样的功能；另外一种可行的方式就是只需将M与T当前的前驱直接交换它们的数据域即可。

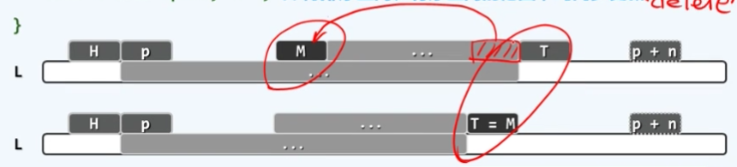
另一问题是有些情况下，对M的搬动操作其实是不必进行的，如果这个最大节点M恰好正是tail的直接前驱
那么它自然已经就位，当然也就无需搬动了。基于这个观察，或许你会倾向于去做这样一种优化：在搬运M前加一条if语句。这样一种改进的方式本身的确是可行的，但是我们并不认为这是一个优化，其中的原因在于，在通常的随机分布下这种情况出现的概率极低（$\ln n/n \to 0$），以致于我们这里所做的这种所谓的优化会得不偿失。

1.4.实现：selectMax()

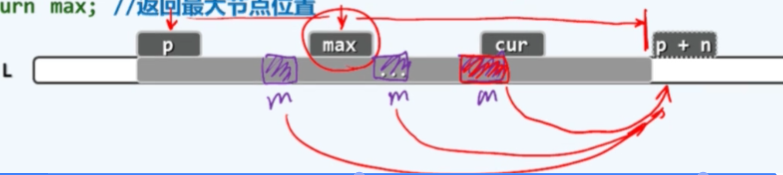
selectMax()接口的实现很朴实，从首节点出发逐一地进行比对，并且在这样的一个过程中记录下当前最大的元素，当我们抵达终点时，这个最终的记录就是我们所要找的最大节点。这个过程可以实现为下面的代码：

template < typename T> //从起始于位置p的n个元素中选出最大者
Posi(T) List<T>::selectMax(Posi(T) p, int n) {
    Posi(T) max = p; //最大者暂定为首节点p
	for (Posi(T) cur = p; 1 < n; n--) //从首节点p出发，将后续节点逐一与max比较
		if (!lt((cur = cur->succ)->data, max->data)) //若当前元素不小于max，则
		    max = cur; //更新最大元素位置记录
	return max; //返回最大节点位置
}

注意到我们这里所采用的比较器是not less than ，也就是不小于（当前元素不小于max），只要当前的这个节点大于或等于目前的max，就需要做相应的更新。这是接口语义要求的，如果序列有最大的元素有多个的话，这样可以返回其中最靠后的那个（秩最大的那个），而这个元素也相应地会被优先地转移到sorted的那部分，就总体效果而言所有的这些重复元素都会依次地转移到相应的位置上去，从而保证算法的稳定性。

1.5性能

选择排序的性能如何呢？这个算法仍是由n次迭代完成的，在第k次迭代中：

• selectMax()为$\Theta(n-k)$，算术级数
• remove()和insertBefore()均为$O(1)$

故总体复杂度为$\Theta(n^2)$。（无论最大元素在哪都需要$n^2$，不分最好最坏情况，因此用$\Theta$）

选择排序居然和起泡排序的效果一样嘛？其实还是有区别的，就这里所涉及的两类操作：节点的移动以及比较大小而言，前者在实际效果也就是常系数的意义下要复杂的多得多，需要花费远远更多的时间，因此这里能够对移动次数做改进，使得每一趟扫描所需要的移动操作从原来的n降至1，实际上是一个非常了不起的改进。那么比较操作同样可以进一步地改进，等到后面的第十章优先级队列中，将会借助精巧的数据结构，使selectMax()可以$\log n$
而不是$n$的时间内完成。

2.插入排序

2.1经验

插入排序也是一种生活中很常见的排序算法，比如在发牌时整理手上的牌[・_・?]，我们可能会这样做：将手牌先按大小整理好，接下来拿到新牌后再按照大小插入到手牌中相应的位置，这其实就是插入排序。

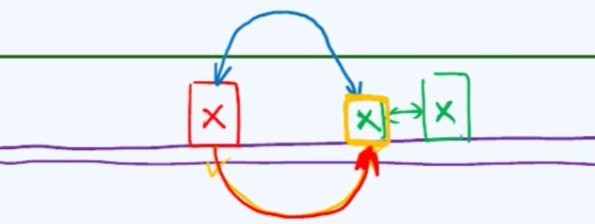
在每次这样的过程中，我们所做的工作无非两步：第一步就是由这条绿色的线所标明的去做一个定位，即寻找到要插入的位置；接下来的动作实际上是两个更小的步骤的组合，首先将更小的牌向左移动以腾出一个空余位置，然后将新牌插入到那个位置。

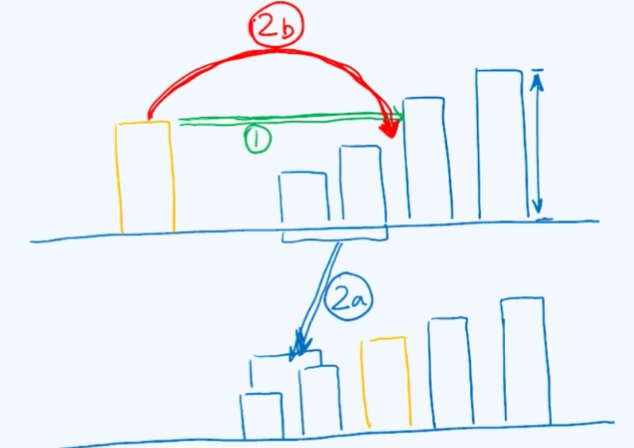
2.2构思

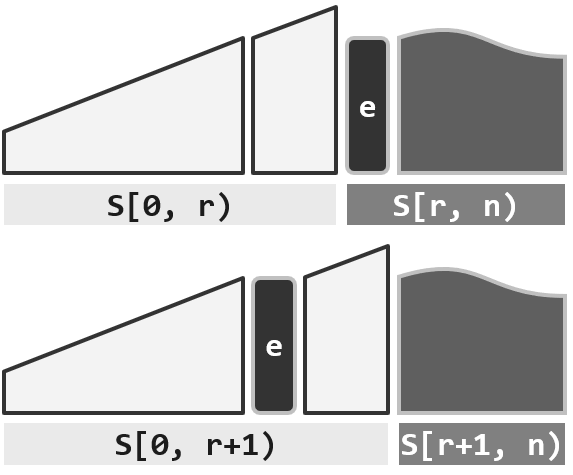
在插入排序算法的整个过程中我们始终将输入序列视作两个部分：有序部分+无序部分

• Sorted + Unsorted

  L[0, r) + L[r, n)

接下来是迭代的过程，在每一次迭代中将当前秩为r的元素e插入到前面的Sorted部分的合适位置，使之保持有序，这样待解决问题的规模就减一，这也是这个算法的不变性。

• 【初始化】置$S_0$为空序列（长度为0） //空序列自然有序

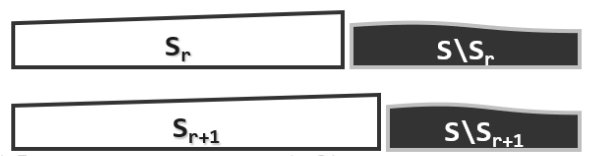
• 【迭代】在有序的$S_r$ = S[0, r)中确定适当位置 //有序序列的查找

  ​ 插入S[r]，得到有序的$S_{r+1}$ = S[0, r] //有序序列的插入

• 如此，可逐步得到：$S_0,S_1,\dots,S_n$，最终，$S_n$ = S[0, n)即排序序列

• 正确性基于以下不变性：$\forall$ 0<= r <= n，$S_r$ = 前r个元素组成的有序序列

2.3对比

介绍到这你可能会有疑问，排序排序和选择排序看起来是一回事啊？但其实它们是截然不同的两种算法，这里先来看一下两者在整体策略上的区别。

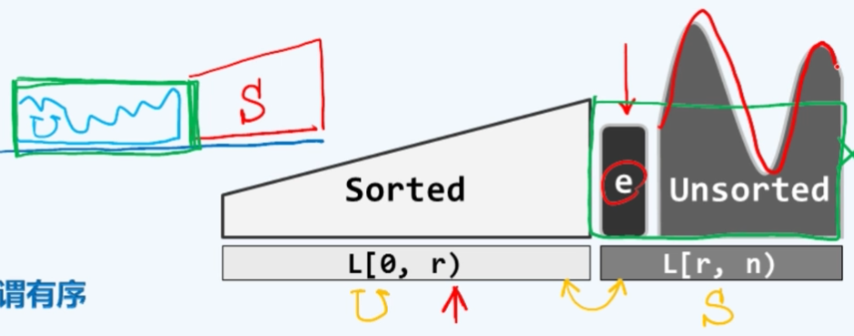
第一个区别：insertion sort有序部分和无序部分的次序左右颠倒，而在selection sort中 有序部分是后缀，无序的部分才是前缀，当然这不是很重要φ(>ω<*) 。

第二个区别：在选择排序中，无序的前缀部分始终保持着一个不变性，也就是无序部分的所有元素都不会超过有序部分的最小元素（第一个）；反观插入排序，并没有这样的规定，有序部分的k个元素仅仅是序列中的前k个元素，要插入的元素可能是任意大小。

2.4.实现

将插入排序的过程实现为下面一段代码：

//列表的插入排序算法：对起始于位置p的n个元素排序，valid(p) && rank(p) + n <= size
template < typename T> void List<T>::insertionSort(Posi(T) p, int n) { 
    for (int r = 0; r < n; r++) { //逐一为各节点
		insertAfter(search(p->data, r, p), p->data); //查找适当的位置并插入
	    p = p->succ; remove(p->pred); //转向下一节点
	}  //n次迭代
}  //仅使用O(1)辅助空间，属于就地算法

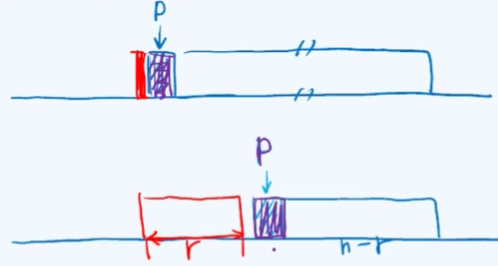
p一开始指向序列的起点，经过一次迭代p后移一位，它始终是有序部分和无序部分的界点。search(p->data, r, p)返回有序部分中不大于p的最大元素（最靠后），接着将值为p->data的节点插入其后（注意这里并不是将p直接插入到那位置），然后将p转向它的后继p->succ，并删除原来的p。

整个算法过程中，除了输入的列表自己本身以外，只需要$O(1)$的额外辅助空间，这种算法被称为就地算法（in-place algorithm ）。

2.5.性能

• 最好情况：完全（或几乎）有序

  每次迭代，只需1次比较，0次交换；累计$O(n)$时间 ！（而选择排序无论好坏都是$\Theta(n^2)$）

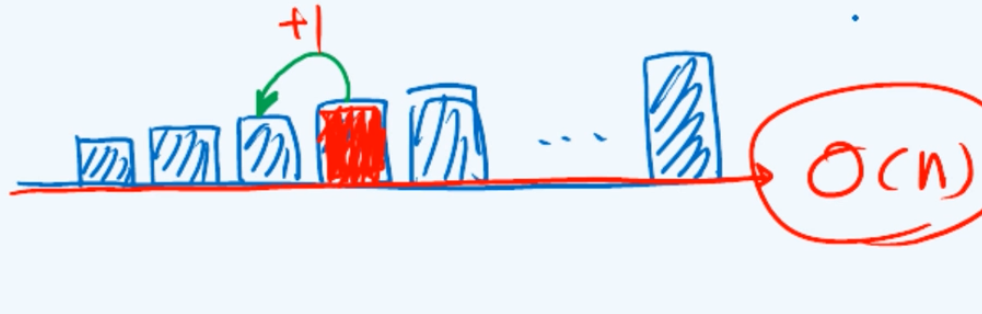
• 最坏情况：完全（或几乎）逆序

  第k次迭代，需要$O(k)$次比较，1次交换；累计$O(n^2)$时间

你可能会想，既然是在一个有序部分中查找，那为什么不用二分查找呢[・_・?]，可以把比较次数降到$O(\log k)$。其实是不行的，因为列表不支持这种循秩访问的方式，而向量是可以的。

那为啥不用向量实现插入排序呢[・ヘ・?]。如果用向量的话，在插入操作时，我们必须将所插入元素之后的元素整体向后移一个单位，这样每次迭代仍然是需要$O(n)$时间，所以就最坏的情况而言，改用向量结构对于插入排序的改进于事无补。

2.6.平均性能

上节分析插入排序在最好和最坏情况下的时间复杂度，那么在一般情况下呢？

假定各元素的取值遵守均匀，独立分布，那么平均要做多少次比较呢？

为此需要采用一种方法：后向分析（backward analysis），我们把时间拉回到某个元素，比如第r个元素刚刚完成插入的那个时刻，在此之前有序前缀长度为r，现在长度为r+1。那么插入这个元素需要花费多少时间呢？由于插入元素的大小是不确定的，而且它插在不同位置上对应的成本也不同。

但是由于我们采用的是均匀独立分布的假设，那么对于现在有序前缀中的r+1个元素中，每个元素都可能是刚刚插入的那个元素，其概率是相等的，为$1/(r+1)$。为了估算刚才那一步迭代的时间成本，我们将每一个元素作为刚插入元素完成插入所对应的成本累计起来，求期望：

$$\left[ r+(r-1)+\dots+3+2+1+0\right]/(r+1)+1=r/2+1$$

于是，整个过程的总体期望是：

$$\left[ 0+1+\dots+(n-1)\right]/2+1=O(n^2)$$

所以插入排序的平均复杂度依然是$O(n^2)$，与它在最坏情况下是同阶的，换而言之，虽然它有最好情况复杂度为$O(n)$，但这种情况发生的概率极低。

2.7.逆序对

最后来看一个与插入排序非常相关的一个概念：逆序对（inversion）。实际上在一个由n个元素构成的序列中，任何两个元素都有可能构成逆序对，其逆序对的总数接近$n^2$。逆序对涉及到两个元素，我们不妨把逆序对这个标记记到后边元素上，对应一个节点p，可以用$i(p)$来表示节点p对应的逆序对数的总和，那么整个序列的逆序对总数为：

$$I=\sum_p i(p)$$

在插入排序中，当要把节点p插入到前面的有序序列S的适当位置时，p所对应的逆序对的个数就是p要经过的比较的次数，$i(p)$其实就是p所对应的查找长度。因此$I$就对应着整个插入排序算法所需要的比较次数的总和，这是算法所消耗时间的主要部分，再加上每n步插入所需要的时间一共是$n$，那么插入排序的复杂度就是$O(I+n)$。

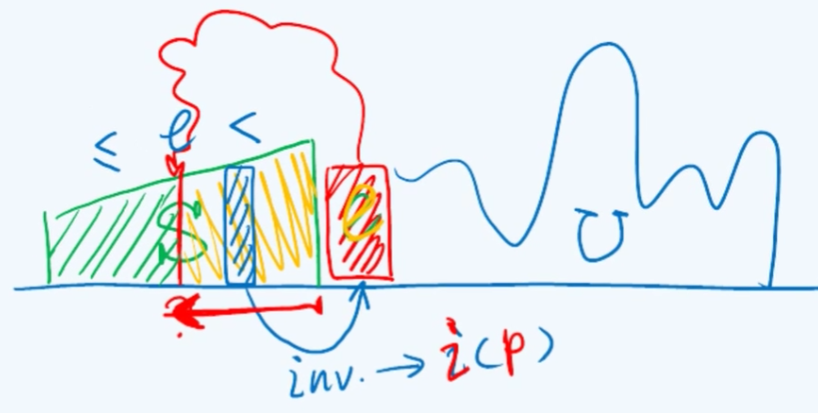
如果把整个序列的逆序对总数$I$作为序列无序程度的度量尺度，那么插入排序insertion sort就可以理解为是通过一次一次的努力去修复这种无序性。因此它的算法复杂度其实不光是取决于问题的规模，而更多的是取决于输入序列本身所具有的特性即它的无序程度，所以这样一种算法也称作输入敏感的（input-sensitive）。在排序算法家族中并非每一种算法都具有这样的一个特性，而插入排序也正因为它具有这样一个特性，而显得非常的独特。在之后要介绍的希尔排序（Shell sort）中，我们将会看到这种输入敏感的特性对于希尔排序整体的性能，乃至这个算法的有效性都是至关重要的。