栈和队列这对孪生兄弟都是线性序列的特例，它们在算法以及应用中都扮演着非常基本而重要的角色，本文主要介绍如何以ADT的形式来定义和规范它们的接口，以及如何借助此前学习过的序列结构（向量与列表）简洁高效地加以实现。

1.栈

1.1操作与接口

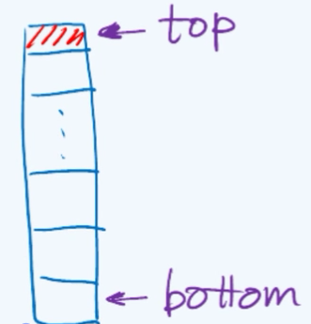
栈结构（Stack）依然是由一组元素组成的线性序列，与一般的序列不同的是，在任何时候我们只能够访问栈中的一个特定元素——最末端那个元素，而其余的元素在当前都是禁止访问的。

通常习惯于将可以访问的开放的这一端，称作顶端top，而不开放的那个盲端称作底部bottom。

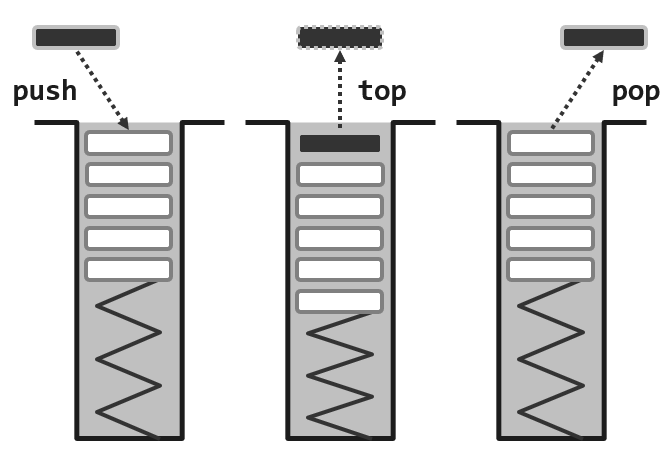
一般意义下的栈以及它的操作可以由下面的一组图来表示，如果需要将某一个新的元素插入其中，那么只能将它作为最顶部的元素插入，这个动作我们也形象地称之为push。反过来如果需要从栈中取出某一个元素，那么也只能取出当前这个顶部的元素，这个元素被取出之后其余元素将依次向前递补，将会出现一个新的顶部元素，这样的一个过程称为pop。当然通常的栈还会提供另一个辅助的接口，查询顶部元素的数值而并不需要将它真正的弹出，那么这样一个动作称之为top。

1.2.操作实例

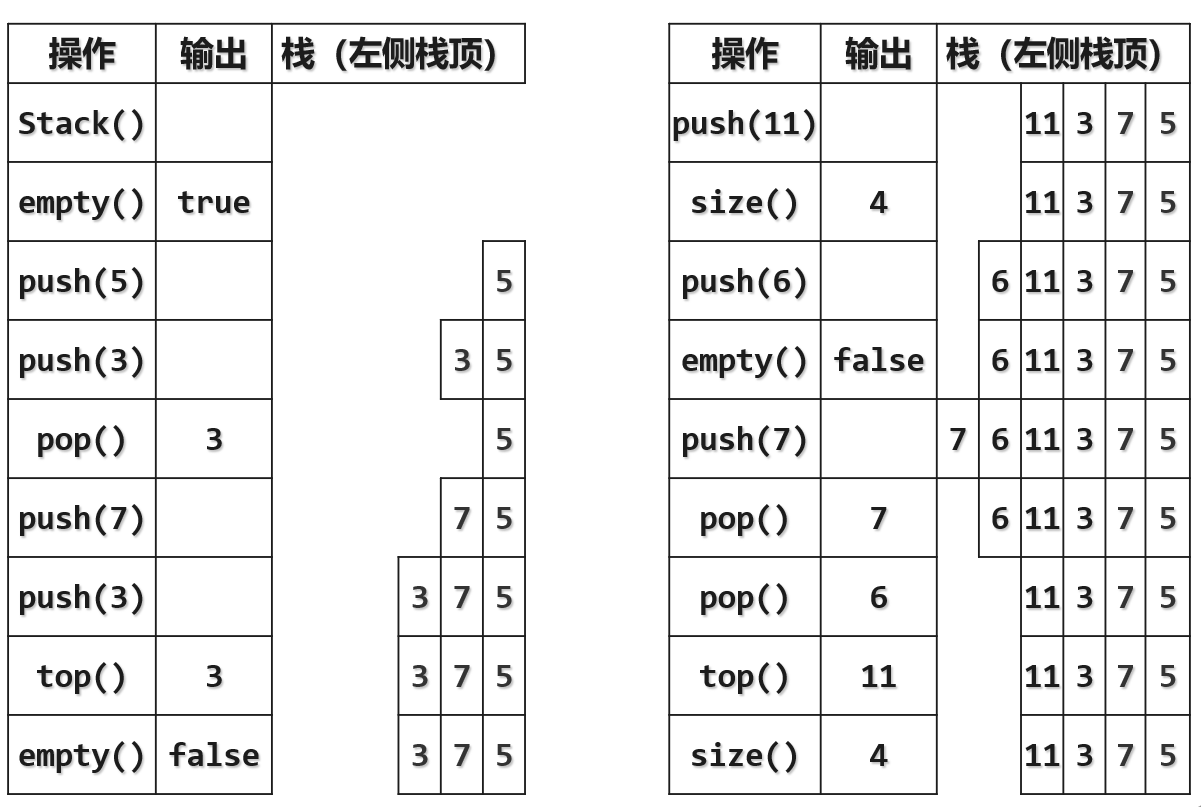
接下来通过一个实例来了解栈结构各种接口的准确功能，以及它们组合之后所能达到的效果。

首先通过构造函数Stack()来创建一个空的栈，调用empty()来检查其是否为空，push(5)在栈中插入第一个元素，图中栈顶是在左侧，栈底是在右侧。push(3)即在栈顶也就是左侧插入元素3，pop(3)则将栈顶的元素删除，size()返回栈序列中元素的个数，top()返回栈顶元素的值。

需要留意的是，栈中元素入栈的出栈的次序，即相对而言后入栈的元素会更早出栈，这也是栈结构的一个非常独特的性质，即后进先出（LIFO），正是因为栈的这种特性使得它在很多算法中都有重要作用。

1.3.实现

实际上既然栈可以视作是序列的一种受限后的特例，那么自然可以通过此前学过的向量或列表结构直接派生而得，即我们完全可以利用向量或者列表来模拟栈以及它的接口行为。

以向量为例，栈中有多少元素，向量中也对应地有多少个元素，如果约定首元素是栈的底部盲端，那么末元素也就是可操作的栈顶，按照这样一个思路就可以简洁地写出栈模板类。

template <typename T> class Stack : public Vector<T> {  //由向量派生
public:   //size()、empty()以及其它开放接口均可直接沿用
	void push(T const & e) { insert(size(), e); }  //入栈
	T pop() { return remove(size() - 1); }  //出栈
	T & top() { return (*this)[size() - 1]; }  //取顶
};

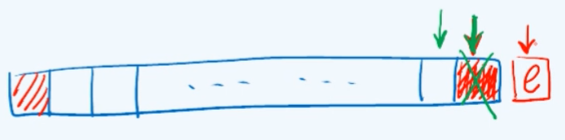
对于向量结构而言无论是插入操作还是删除操作，所需要的时间都线性正比于插入和删除位置的后继的数目。对于栈结构，无论是插入操作还是删除操作都是在向量的末端进行，因此所有这些操作接口的时间复杂度都是常数的，即为$O(1)$。如果将向量的首元素作为栈顶，那么每次插入和删除操作的时间复杂度就会变成$O(n)$。

2.队列

队列（queue）也是一种特殊的线性序列，想想生活中机场安检窗口的队列或者超市等待付款的队列，用数据额结构的语言来说它们都构成一个线性的序列，与栈一样它也是一个受限的序列，不同的是队列的一端只能够出，另一端只能怪进。通常，允许插入的那一端被称作尾部，允许删除的一端被称为头部。

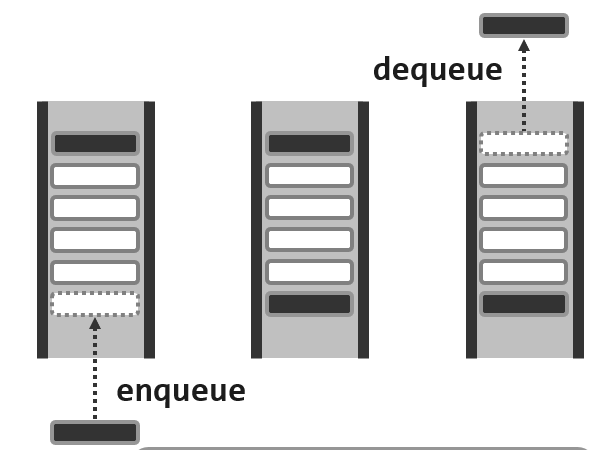
队列也是受限的序列：
- 只能在队尾插入（查询）：enqueue() + rear()
- 只能在队头删除（查询）：dequeue() + front()
队列中元素入队和出队的次序与栈相反：
- 先进先出（FIFO）
- 后进后出（LILO）

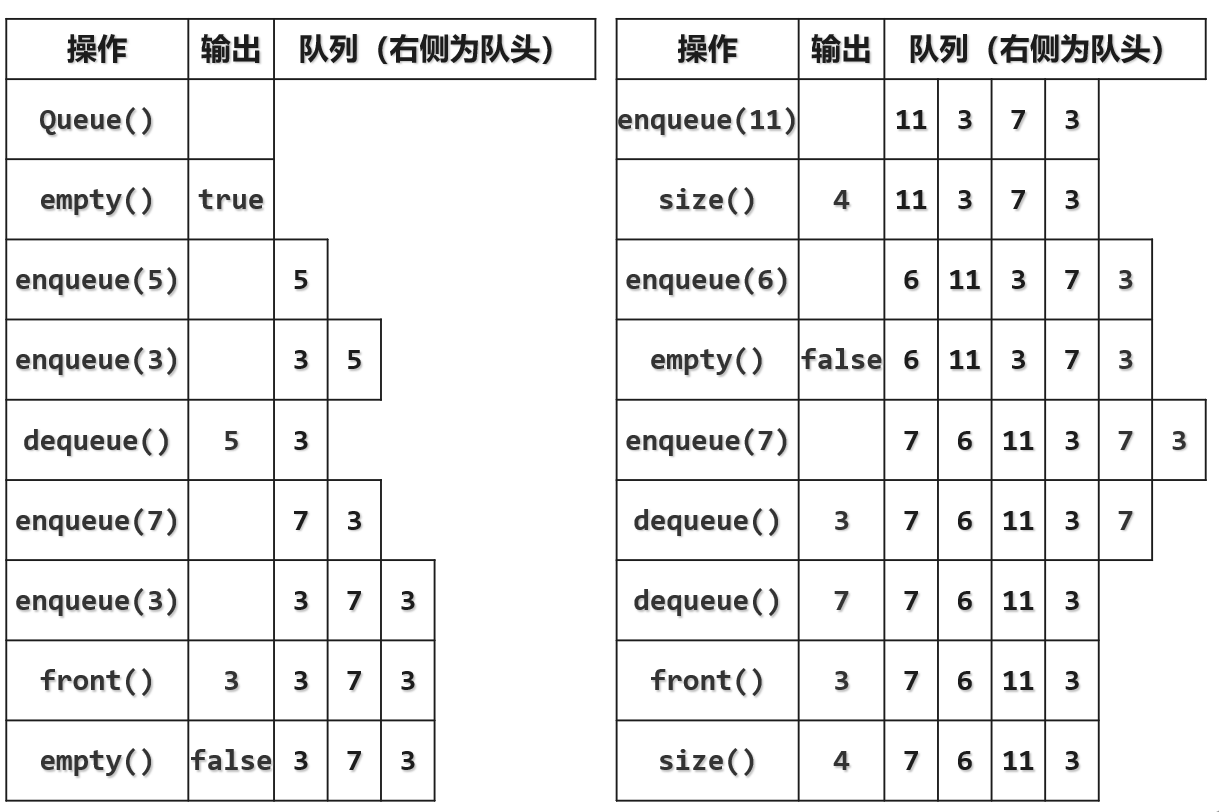
下面是一个队列的操作具体事例：

2.2.实现

与栈同理既然队列也是属于序列，自然可以利用此前已经实现的最基本的向量以及列表结构直接派生而得，这里选用列表来实现队列。

template <typename T> class Queue : public List<T> {  //由列表派生
public:   //size()与empty()以及其它开放接口均可直接沿用
	void enqueue(T const & e) { insertAsLast(e); }  //入队
	T dequeue() { return remove( first() ); }   //出队
	T & front() { return first()->date; }   //查询队首元素
};

由于列表结构的特性，无论是enqueue() ，dequeue()还是front()这些接口都能够在常数的时间内完成，即$O(1)$的时间。

这种基于以前的工作来进一步完成新的任务的思路，不仅使得我们的工作可以快速推进，而且使得整个工作的系统性和安全性都能得到保障(ง •_•)ง

队列结构在此后的图算法以及其它的场合都有广泛的应用，所以这里只是首先简要地介绍它的接口定义，以及它在C++中的实现方式。