数据结构与算法（8）栈应用

栈结构的经典应用场合大致可以分为以下四类：

• 逆序输出

  • conversion：

  • 输出次序与处理过程颠倒；递归深度和输出长度不易预知

• 递归嵌套

  • stack permutation + parenthesis

  • 具有自相似的问题可递归描述，但分支位置和嵌套深度不固定

• 延迟缓冲

  • evaluation

  • 线性扫描算法模式中，在欲读足够长之后，方能确定可处理的前缀

• 栈式计算

  • RPN

  • 基于栈结构的特定计算模式

1.进制转换

问题描述：给定任一10进制非负整数，将其转换为$\lambda$进制表示形式。

解法我们都很熟悉，即短除法：对给定的数做除法，留商取余，所得的余数再逆序输出。

这样一个过程在用代码实现时一个问题需要考虑：计算的过程是由上而下的，而输出的过程是由下而上的，如果不借助对数我们很难预测最终会有多少个数位，也就是整个计算的深度到底有多少，那这个问题该如何解决呢？

回顾上篇文章中介绍的栈结构，我们只需引入一个栈，在计算的过程中，我们每得到一个数位（余数），就通过push()使它入栈，那么这些数位入栈的次序恰好就是它们被计算出来的次序（在图中是自上而下）。而栈的特性是后进先出（LIFO），一旦计算终止，我们就可以通过一系列pop()操作将这些数位按刚才的数位的逆序（在图中是自下而上）输出出来，从而得到所需要的结果。

void convert(Stack<char> & S, _int64 n, int base) {
	//薪进制下的数位符号，可视bae取值范围适当扩充
	static char digit[] = 
	{ '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F' };
	while (n > 0) {   //由低到高，逐一计算出薪进制下的各数位
		S.push( digit[ n % base ] );  //余数（对应的数位）入栈
		n /= base;   //n更新为其对base的除商
	}
}

2.括号匹配

括号匹配这个问题可以归为递归嵌套式问题，以括号匹配为代表的这类问题它们的共同特点是，具有某种意义上的自相似性，即它们的某一个局部往往和整体具有某种共性，同时这种局部作为分支它的位置以及嵌套的深度却难以在事先固定或者确定。

括号匹配是合法表达式的必要条件之一，下面是一个实例：

我们的任务是给定任意一个含有括号的表达式如何来判定它是否是匹配的，为了简化问题不妨将括号之外的其余符号都暂时地忽略掉，只需要做一次线性扫描的预处理即可，这样就可以集中注意处理括号匹配的情况。

2.1.构思

为了得到这个问题的有效解法，我们或许应该继续沿用不断将问题简化的总体策略。为此需要首先来考察最基本的平凡情况：如果一个表达式不含任何的括号，从而实质上等价于一个空串，那么它自然是匹配的。

接下来我们注意到这样一个事实：如果某一个表达式E已经是括号匹配的，那么在它的左侧和右侧添加一对匹配的括号，整体依然将是匹配的；如果两个表达式E和F已经是各自匹配的，那么只要将它们串接起来就可以得到一个更大的匹配表达式。

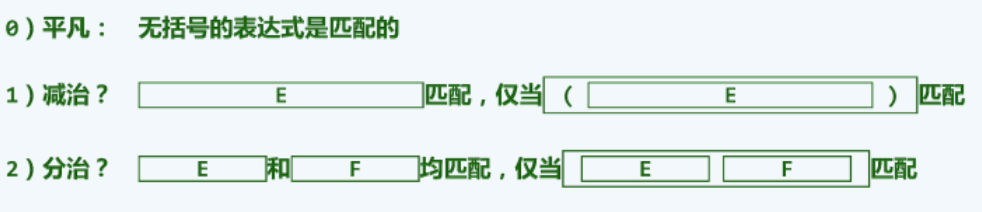
然而很遗憾这两个性质都不能使得我们很好地运用此前所学的减而治之或者分而治之的策略。因此这两条性质只能作为括号匹配判断的必要条件而非充要条件，从逻辑推理的方向来看它是由左侧的前命题推向右侧的后命题，与简化问题的方向背道而驰。

而且它们也存在反例，这就让减而治之和分而治之都是行不通的。因此为了真正使这个问题能够得到有效的简化，必须发现并且借助这个问题所蕴含的某种充分性。

一种可行的方法是将以上的减而治之的策略颠倒过来，不是去试图减除一个表达式最外围的一对括号，而是试图去减除其中相互紧邻的一对左右括号。如果在一个表达式中能够发现一对彼此紧邻的左右括号，那么在将这对括号减除之后，剩余的部分是否匹配与此前的表达式是否匹配必然是互为充要条件的。

那么如何找到这样一对括号呢？另外，更重要的是如何使得这种简化能够持续地进行下去呢？

实际针对上面的情况，正是栈可以大显身手的时候，借助栈结构的算法过程原理可以表示为下图。如果这是我们所使用的栈，那么其中所包含的就是我们已经扫描过但是仍待处理的部分，其中只需保存左括号。在接下来的扫描中一遇到左括号就令它入栈；而一旦遇到右括号不仅不需要令它入栈，反而应该令栈顶的那个左括号出栈。

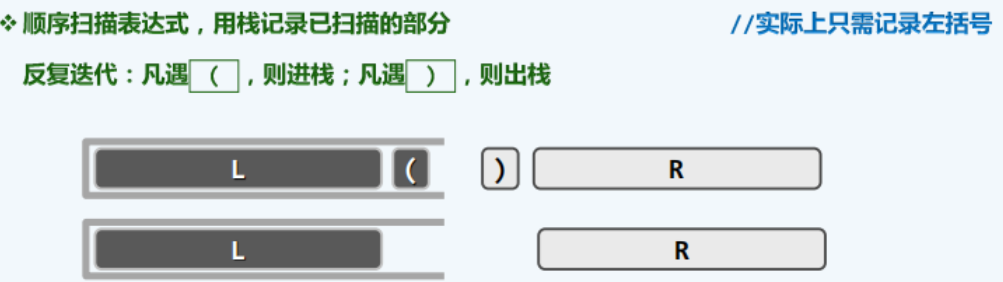
这样就刚好实现了上述的可行方法，算法的确可以持续地如此往复进行下去。如果最后一个括号被处理之后，整个栈恰好变空，那么就意味着原来的表达式是匹配的；反之，无论到最后栈非空或者在中途某个阶段提前变空，我们都可以判定原来的表达式是不匹配的。

2.2.实现

上节的构思可以具体兑现为这样一段代码：

bool paren(const char exp[], int lo, int hi) {  //exp[lo, hi)
	Stack<char> S;   //使用栈记录已发现但尚未匹配的左括号
	for (int i = lo; i < hi; i++)   //逐一检查当前符号
		if ('(' == exp[i]) S.push(exp[i]);   //若遇左括号，则进栈
		else if (!S.empty()) S.pop();    //否则如果遇右括号，且栈非空，则令栈顶的左括号出栈
		else return false;   //否则（遇右括号是栈已空），必不匹配
	return S.empty();   //最终，栈空当且仅当匹配
}

为了判别low与high之间的这样一段表达式是否括号匹配，需要引入一个名为S的栈。以下的这个循环逐一地检查每一个字符，如果是左括号就令它入栈，否则就试图弹出栈顶，如果它的确存在的话应该就是与当前这个右括号匹配的那个左括号，而如果此时栈已经提前变空那么就意味着整个表达式失配，可以断定此时的失配是由于某一个右括号缺少与之匹配的左括号。

当处理完所有的字符并退出循环的时候，需要检查栈在当前是否是空的，只有当栈恰好为空时才说明表达式是匹配的，否则可以断定原来那个表达式是不匹配的，且是属于某一左括号缺失与之配对的右括号的情况。

2.3.反思与拓展

为更好地理解这个算法，我们不妨来看一个具体的实例：

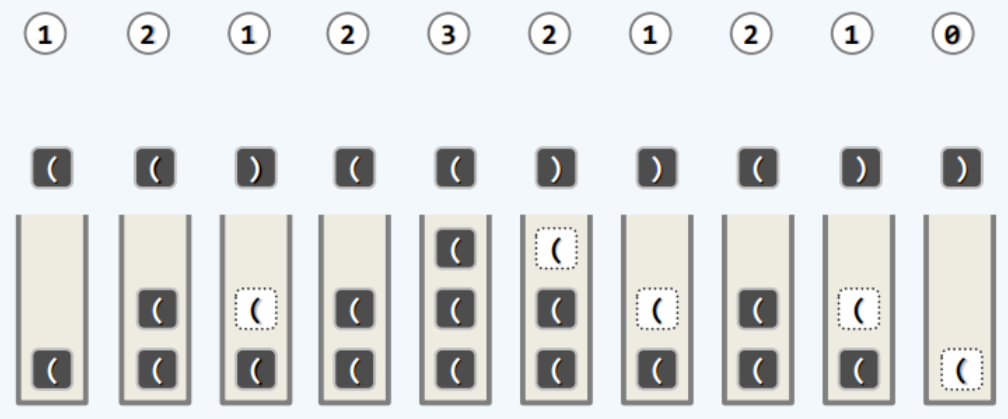
在理清这个实例的执行过程后，你可能会质疑我们为什么要使用栈呢[・_・?]。就这样一个特定的问题而言，只需借助一个简明的整数计数器就足以完成刚才的算法任务。如果令计算器初始为0，将算法的过程对应过来，若遇左括号计数器就加1；若遇右括号计算器就减1。最终如果计数器为0，则表达式匹配；如果计数器不为0，或在中途出现负数，则表达式不匹配。

实际上这个计数器所反映的就是刚才我们所使用的那个栈在任何时刻的规模，这样就不难理解其中的必然性了。那么既然如此我们为什么不使用更加简明的计数器，而要使用更为复杂的栈结构呢[・_・?]

这背后的原因在于采用栈结构可以便捷地推广至多种括号并存的情况，这时如果想要使用多个计数器也是行不通的，比如一个简单的反例[ ( ] )，因为如果孤立地通过计数器来考察方括号或者是圆括号，两个计数器都是可以正常工作并且在最终复位为0的，而这个表达式显然是不匹配的。

通过下面这个实例来解释这个算法如何扩展到多个括号并存的情况。当遇到一个左括号，无论是什么形式都放入栈中；遇到一个右括号，则判断此时栈顶的左括号是否与它匹配，若匹配则令栈顶的左括号出栈。

同样地在经过了这样一趟线性的扫描之后，只有当栈最终为空，我们才可以断定原来这个包含多种括号的表达式是匹配的。反过来这时括号不匹配的情况相对于此前单括号的情景要多出一种，即当遇到右括号时，发现此时栈顶的左括号与之不匹配，如刚才举的反例[ ( ] )，则表达式必是不匹配的，因为实际上这样每次“消去”的一对括号必是紧邻的一对括号。

扩展后括号匹配算法可以实现为下面一段代码：

bool paren(const char exp[], int lo, int hi) { //表达式括号匹配检查，可兼顾三种括号
	Stack<char> S; //使用栈记录已发现但尚未匹配的左括号
	for (int i = lo; i <= hi; i++) /* 逐一检查当前字符 */
	    switch (exp[i]) { //左括号直接进栈；右括号若与栈顶失配，则表达式必不匹配
	        case '(': case '[': case '{': S.push(exp[i]); break;
		    case ')': if ((S.empty()) || ('(' != S.pop())) return false; break;
		    case ']': if ((S.empty()) || ('[' != S.pop())) return false; break;
		    case '}': if ((S.empty()) || ('{' != S.pop())) return false; break;
		    default: break; //非括号字符一律忽略
	    }
	return S.empty(); //整个表达式扫描过后，栈中若仍残留（左）括号，则不匹配；否则（栈空）匹配
}

最后需要指出的是，实际上这样一种拓展还可以进一步地进行，也就是并不限于某几种特定的括号，甚至不需要对这些括号到底有多少种做出限定，就像在HTML语言中那样只要表达式中能够按照合理的语法，就能够定义任何一种匹配标志，我们都可以来进行这种意义上的匹配检查。

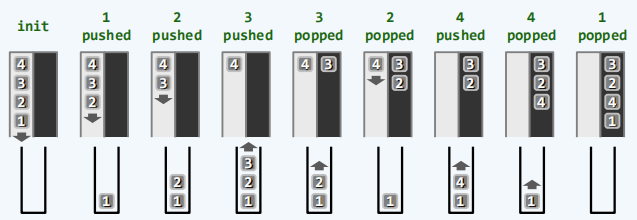
3.栈混洗

本节介绍一个与上一节括号匹配问题非常相关的问题：栈混洗问题。栈混洗就是按照某种约定的规则对栈中的元素进行重新的排列。初始情况下所有的元素都存在栈A中，这里约定分别用尖括号和方括号来表示栈顶以及栈底，栈混洗的目标是将所有这些元素都通过某种方式转入到另一个初始为空的栈B中，为此需要借助一个中转栈S。

• 栈 A = $<a_1,a_2,\dots,a_n]$、B = S = $\varnothing$

• 只允许的操作：

  • 将A的顶元素弹出并压入S； //S.push(A.pop())
  • 或将S的顶元素弹出压入B。 //B.push(S.pop())

• 若经过一系列以上的操作后，A中元素全部转入B中；

  则B = $[a_{k1},a_{k2},\dots,a_{kn}>$则称之为A的一个栈混洗（stack permutation）

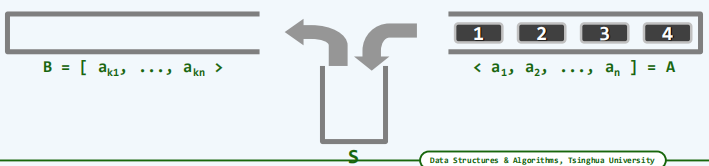
在遵守以上规则的前提下同一输入序列可能导出不同的栈混洗序列，比如 A = <1, 2, 3, 4]就可能得到：

B = [1, 2, 3, 4>，[4, 3, 2, 1>，[3, 2, 4, 1>，……

3.1.计数

那么长度为n的序列，可能的栈混洗总数$SP(n)$为多少呢？

假定输入栈 A = < 1, 2, 3, ……, n ]，关注1号元素，它第一个被推入栈S中，假设它是第K个从S出栈的元素，当它出栈后S已为空，相应地A剩余最靠底的n-k个元素。此时B中最靠底的k-1个元素和A中最靠底的n-k个元素，它们的栈混洗实际上是相互独立的。

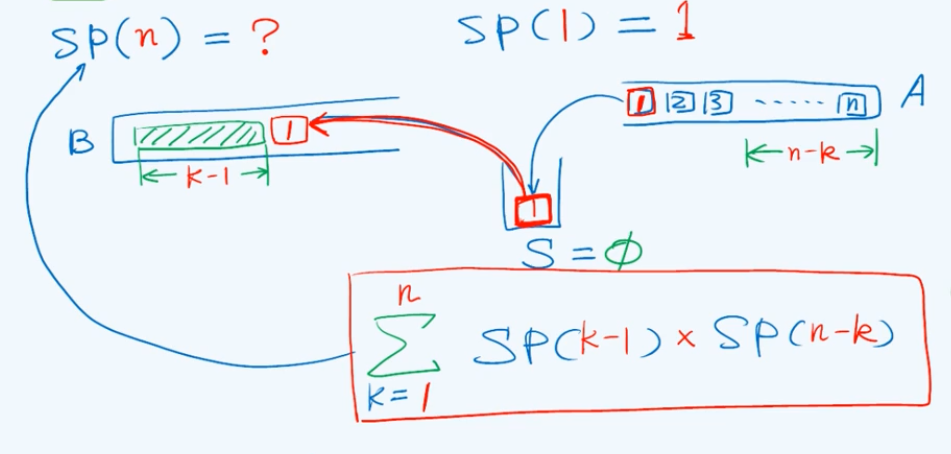
因此对应于1号元素作为第k个元素被推入B中的情况，对应的栈混洗总数就应该是这两个相互独立的子序列所各自对应的栈混洗总数的乘积$SP(k-1)\times SP(n-k)$，又k可以取1到n，因此长度为n的序列，可能的栈混洗总数为：

$$SP(n)=\sum_{k=1}^n SP(k-1)\times SP(n-k)=catalan(n)=\frac{(2n)!}{(n+1)!n!}$$

3.2.甄别

对于输入序列< 1, 2, 3, ……, n ] 的任一个排列 [$p_{1},p_{2},\dots,p_{n}$ > 如何来判断它究竟是不是一个合法的栈混洗？

先从简单的例子入手，考虑由三个元素所构成的一个输入序列，则$SP(3)=5$，而三个数的全排列为$3!=6$，对于这种情况有一种排列不是栈混洗，显然不是栈混洗的排列是[ 3, 1, 2>。

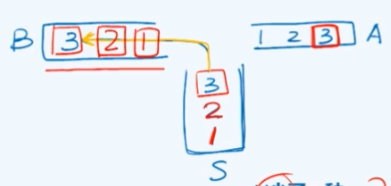
实际上任意的三个元素能否按照某种相对的次序出现在最终的栈混洗中，与其它的元素实是无关的，因此推而广之对于任何三个互异的整数 $1\le i < j<k \le n$，如果在某个排列中出现了 k i j，那么它就必然不是栈混洗。这是栈混洗所必须禁止的一种特征，称之为禁形。

Kunth在他的《The Art of Computer Programming》中证明了 一个排列permutation是一个栈混洗的充要条件就是其中不含禁形。

由此可以导出一个算法：不断地枚举所有的i j k的组合，但其复杂度高达$O(n^3)$。进一步地可以将这样一个判别的依据简化：判断栈混洗的充要条件是，对于每一对互异的i<j，在排列中不会出现 j+1 i j 这样的一个模式，由此导出的枚举算法的复杂度是$O(n^2)$。

而借助栈结构可以实现一个线性时间$O(n)$的甄别算法，其思想是：完全按照栈混洗的定义引入三个栈，并且通过对栈混洗过程的模拟以一种验证的方式来判别某一个排列是否的确为栈混洗。具体地对于输出序列中的任何一个元素，都采用一种贪心算法的原则以S为中介 将其从A转移至B中，只要这个贪心的过程能够持续进行并最终将所有的元素顺利地从A转入B中，那么就可以判断它是一个栈混洗。反之每次通过pop操作试图从S中弹出当前的元素时，如果S已经变空，或者要弹出的元素不是S栈顶的元素，就可以立即判断这个栈混洗是非法的。

//参照LeetCode面试题31：栈的压入，弹出序列
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
    stack<int> S;
    auto i=pushed.begin();
    for(auto j=popped.begin();j!=popped.end();j++){
        while(S.empty()||S.top()!=*j)
        if(i==pushed.end())
          return false;
        else S.push(*i++);
        S.pop();
    }
    return true;
}

3.3.栈混洗与括号匹配的关系

n个元素的任何一个栈混洗都对应于中转栈S的n次push操作以及n次pop操作所构成的一个序列。如果将每push都换成一个左括号，而将每次pop对应一个右括号，就会发现同一元素所对应的那对push、pop操作都恰好对应于一对彼此匹配的括号。反过来由n对括号所构成的任何一个合法的表达式，实际上也可以解释为对n个元素进行栈混洗的一个合法的过程，也相应地对应于某一个输出的栈混洗。

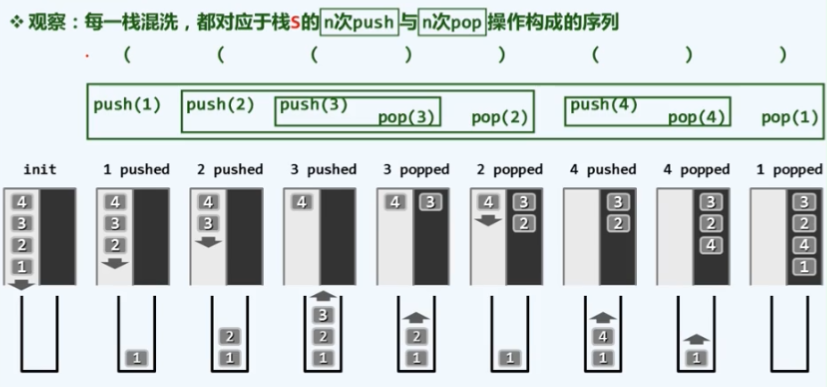
因此合法的栈混洗序列与合法的括号匹配表达式之间存在一个一一对应的关系，n个元素的栈混洗有多少种n对括号所能构成的合法表达式也就有多少种。

4.中缀表达式求值

中缀表达式求值问题属于栈结构的另一种典型应用场合：延迟缓冲，在中缀表达式求值这样一类线性扫描算法中我们并不能保证处理的速度和读取的速度同步，而往往是需要预读足够多的信息之后才能够确定足以处理的一个前缀。这节中只考虑语法正确的算术表达式，即给定任一语法正确的表达式S，计算出与之对应的数值。

4.1.表达式求值

回顾括号匹配算法：对于任何的一个表达式，在其中找到一对彼此紧邻也因此相互配对的括号，将这样一对括号删去，从而在剩余表达式与原先表达式在是否匹配上互为充要条件的前提下，使得问题的规模也就是括号的对数有所减少。

对于表达式求值，我们依然要在表达式中寻找一个能够优先计算的子串，并且对它进行计算，然后将计算所得的数值重新放置在这个位置上，经过如此的转换之后，新的表达式的数值与原表达式的数值保持一致。如果将一个表达式的复杂度定义为其中包含的运算符的数目，那么这个过程依然是一个减而治之（decrease and conquer）的过程。因此这个算法具有单调性，最终将消除掉所有的运算符，从而得到最终的数值。下面是个具体的例子（计算次序由下到上）：

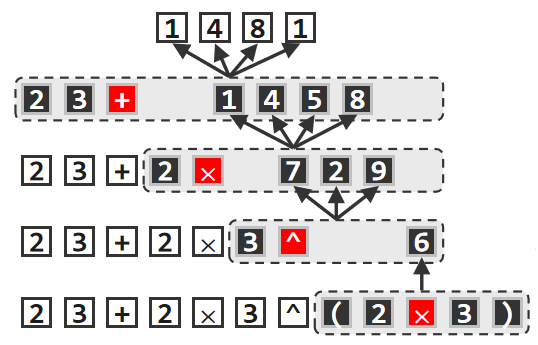
这样一个计算过程虽然在纸面上简便易行，但是如果面对比较长甚至非常长的表达式就将碰到很大的困难，这个困难就在于我们很难定位当前可以计算的那个运算符。如果以一种线性扫描的次序来处理表达式，每当扫到一个运算符的时候都未必能够确认它已经是可以计算的，也就是说计算次序未必与扫描的次序完全一致。

对于这样的一类问题，一种行之有效的办法就是借助栈结构，只需将所有已经扫描过的部分保存为一个栈，在所有已经扫描过的部分中有一些是能够及时处理的即在局部具有足够高的优先级，并且已经计算过的部分；而已经扫描过但是还不足以判断能够计算的部分将通过这个栈被缓冲起来，而我们的策略就是逐步地将尚未扫描的部分扫描并且处理掉。

求值算法 = 栈 + 线性扫描：

自左向由扫描表达式，用栈记录已扫描的部分（含已执行运算的结果）
   在每一字符处
       while(栈的顶部存在可优先计算的子表达式)
         该子表式退栈；计算其数值；计算结果进栈
   当前字符进栈，转入下一字符

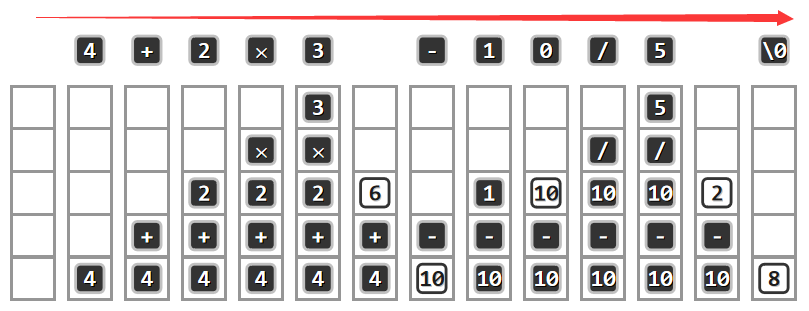
相对于此前那种纸面操作这样一个过程更加接近于机器能够自动实现的层次，然而离最终的目标还有差距，原因在于我们每次在栈顶检出这个可以计算的子表达式，无论是2乘3还是10除以5都不是那么自然，而诀窍在于将运算符和运算数分别对待，即将运算符和运算数分别存入两个栈中。

4.2.实现

//定义优先级表
const char pri[9][9] = {
	//                当前运算符
	//        +   -   *   /   ^   !   (   )  \0   
	/* + */{ '>','>','<','<','<','<','<','>','>' },
	/* - */{ '>','>','<','<','<','<','<','>','>' },
	/* * */{ '>','>','>','>','<','<','<','>','>' },
	/* / */{ '>','>','>','>','<','<','<','>','>' },
	/* ^ */{ '>','>','>','>','>','<','<','>','>' },
	/* ! */{ '>','>','>','>','>','>',' ','>','>' },
	/* ( */{ '<','<','<','<','<','<','<','=',' ' },
	/* ) */{ ' ',' ',' ',' ',' ',' ',' ',' ',' ' },
	/* \0*/{ '<','<','<','<','<','<','<',' ','=' }
	//(栈顶运算符)
};

//解析数字
void readNumber(char*& p, Stack<float>& stk) { //将起始于p的子串解析为数值，并存入操作数栈
	stk.push((float)(*p - '0')); //当前数位对应的数值进栈
	
	while (isdigit(*(++p)))   //只要后续还有紧邻的数字（即多位整数的情况），则
		stk.push(stk.pop() * 10 + (*p - '0')); //弹出原操作数并追加新数位后，新数值重新入栈
	
	if ('.' != *p) 
		return; //此后非小数点，则意味着当前操作数解析完成
	
	float fraction = 1; //否则，意味着还有小数部分
	while (isdigit(*(++p))) //逐位加入
		stk.push(stk.pop() + (*p - '0') * (fraction /= 10)); //小数部分
}

// 由运算符得出编号
int optr2rank(char op) {
	switch (op)
	{
	case '+':return 0;
	case '-':return 1;
	case '*':return 2;
	case '/':return 3;
	case '^':return 4;
	case '!':return 5;
	case '(':return 6;
	case ')':return 7;
	case '\0': return 8;
	default:exit(-1);
	}
}

//比较运算符的优先级
char orderBetween(char op1, char op2) {
	return pri[optr2rank(op1)][optr2rank(op2)];
}

//执行二元运算
float calcu(float a, char op, float b) { 
	switch (op) {
	case '+': return a + b;
	case '-': return a - b;
	case '*': return a * b;
	case '/': if (0 == b) exit(-1); return a / b; //注意：如此判浮点数为零可能不安全
	case '^': return pow(a, b);
	default: exit(-1);
	}
}

//执行一元运算
float calcu(float b) { 
	if (b < 1.01)
		return 1;
	return b*(calcu(b-1)); //目前仅有阶乘，可照此方式添加	
}

//算法主体部分，中缀表达式求值
float evaluate(char* S ) {
	Stack<float> opnd;  //运算数栈
	Stack<float> optr;  //运算符栈
	optr.push('\0');    //尾哨兵'\0'也作为头哨兵入栈
	while (!optr.empty()) {  //逐个处理各字符，直至运算符栈空
		if (isdigit(*S))     //若当前字符为操作数，则
			readNumber(S, opnd);   //读入（可能多位的）操作数
		else    //若当前字符为运算符，则视其余栈顶运算符之间优先级的高低
			switch(orderBetween(optr.top(), *S)){
			case '<': //栈顶运算符优先级更低时
				optr.push(*S); S++; //计算推迟，当前运算符进栈
				break;
			case '=': //优先级相等（当前运算符为右括号或者尾部哨兵'\0'）时
				optr.pop(); S++; //脱括号并接收下一个字符
				break;
			case '>': { //栈顶运算符优先级更高时，可实施相应的计算，并将结果重新入栈
				char op = optr.pop();  //栈顶运算符出栈并续接至RPN末尾
				if ('!' == op) { //若属于一元运算符
					opnd.push( calcu( opnd.pop() )); //实施一元计算，结果入栈
				}
				else { //对于其它（二元）运算符
					float pOpnd2 = opnd.pop(), pOpnd1 = opnd.pop(); //取出后、前操作数 
					opnd.push( calcu( pOpnd1, op, pOpnd2 ) ); //实施二元计算，结果入栈
				}
				break;
			    }
		    }
	   }
	return opnd.pop();
}

5.逆波兰表达式

5.1.RPN

逆波兰表达式（Reverse Polish notation，RPN），是一种由波兰数学家Jan Łukasiewicz在1920年引入的数学表达式，在逆波兰表达式中，所有操作符置于操作数的后面，不需要括号来标识操作符的优先级。在RPN中我们原先使用的运算符优先级和括号强制指定优先级都不存在了，因此RPN更适合机器来完成表达式的计算。

• 在由运算符（operator）和操作数（operand）组成的表达式中不使用括号（parenthesis-free）即可表示带优先级的运算关系。

• 相对于日常使用的中缀式（infix），RPN被称为后缀式（postfix）
• 作为补偿，须额外引入一个起分隔作用的元字符（比如空格）

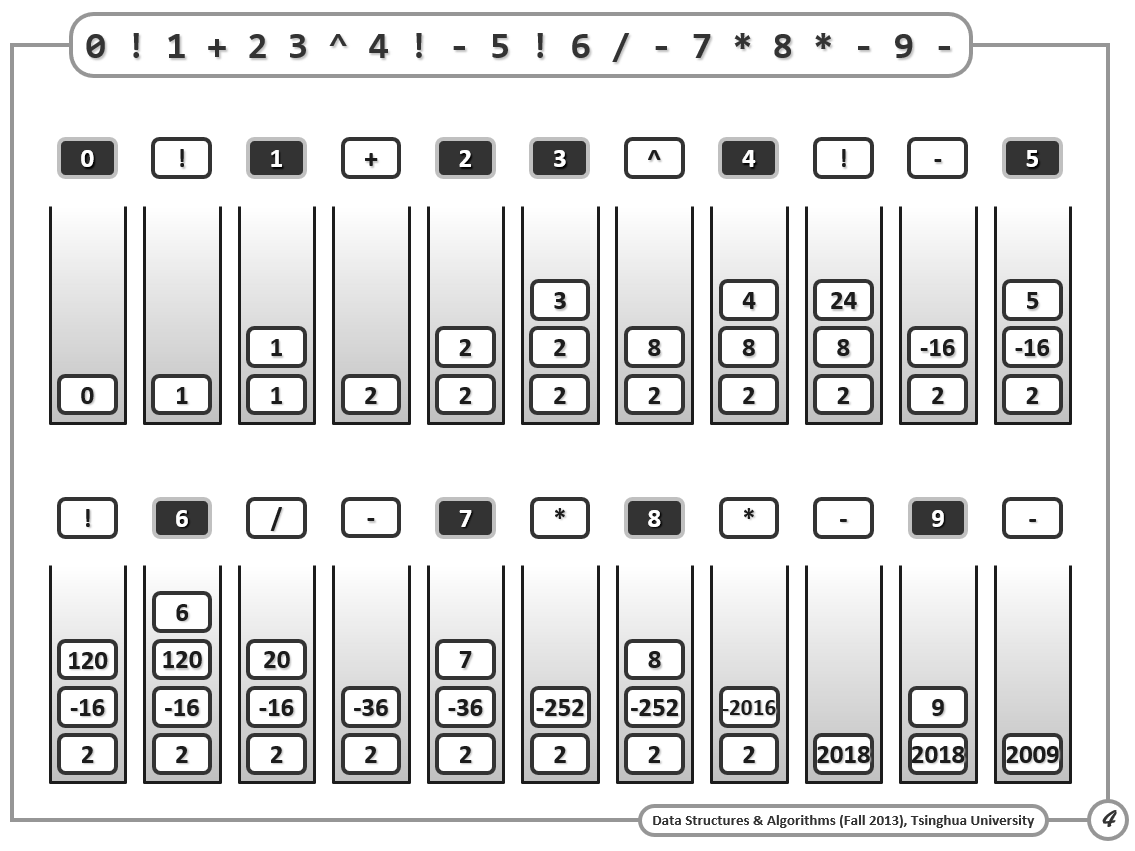
相比于上节的中缀表示式计算，RPN的计算显得十分简便，只需引入一个辅助栈：

rpnEvaluate(expr) { //假定RPN表达式epxr的语法正确
    引入栈S，用于存放操作数；
    while(expr尚未扫描完毕){
        读入expr的下一个元素x;
        if(x是操作数)
            将X压入S;
        else{  //x是运算符
            从栈中弹出运算符x所需数目的操作数;
            对弹出的操作数实施x运算，并将运算结果重新压入S;         
        }
    }
    返回栈顶; //也是栈底
}

5.2.中缀表达式向RPN的转换

中缀表达式向逆波兰表达式的转换可以按以下过程实现：

主要注意的是：在转换完成后，操作数的次序不会发生变换，而运算符的次序可能发生变换。

转换的具体算法实际上可以直接借助上节计算中缀表达式的算法，它在计算中缀表达式结果的同时，实际上也完成了向RPN的转换，重点关注下面代码的第6行和第12行。

float evaluate(char* S string *RPN) {
    /*.................................*/
	while (!optr.empty()) {  //逐个处理各字符，直至运算符栈空
		if (isdigit(*S)) {    //若当前字符为操作数，则
			readNumber(S, opnd);
            *(RPN++) = to_string(opnd.top());  //将其压入RPN
		else    //若当前字符为运算符
			switch(orderBetween(optr.top(), *S)){
			/*..............................*/
			case '>': { //栈顶运算符优先级更高时，可实施相应的计算，则
				char op = optr.pop();
                *(RPN++) = op;//在执行相应的同时将其压入RPN
				/*.............................*/
		    }
	   }
	return opnd.pop();
}