数据结构与算法（10）二叉树的遍历

• 遍历：按照某种次序访问树中各节点，每个节点被访问恰好一次。

  $T=V\cup L \cup R=\{root\} \cup L_ subtree(T) \cup R _ subtree(T)$

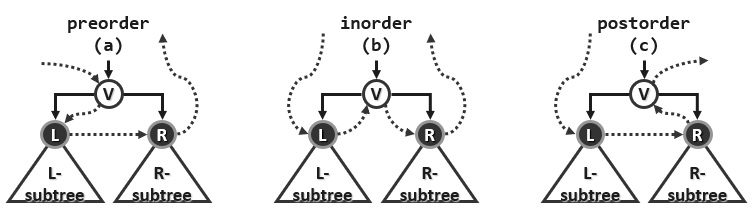
• 遍历结果 ~ 遍历过程 ~ 遍历次序 ~ 遍历策略

  • 先序遍历：V | L | R
  • 中序遍历：L | V | R
  • 后序遍历：L | R | V
  • 层次遍历：自上为下，先左后右

1.先序遍历

1.1递归

以上三种典型的遍历策略都不难实现，因为它们的定义本身就是递归式的，以先序遍历为例，只需四句就可以实现。

template <typename T, typename VST> //元素类型、操作器
void travPre_R(BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法（递归版）
	if (!x) return;
	visit(x->data);
	travPre_R(x->lc, visit);
	travPre_R(x->rc, visit);
}  //T(n) = O(1) + T(a) + T(n-a-1) = O(n)

这个算法的时间复杂度是线性的，即$O(n)$，然而这只具有渐近的意义。在实际的运行过程中，因为递归程序的实现机制，并不可能做到针对具体的问题来量体裁衣，而只能采用通用的方法。在运行栈中尽管每一个递归实例都的确只对应于一帧，但是因为它们必须具有通用格式，所以并不能做到足够的小。而针对于具体的问题，只要我们能够进行精巧的设计，完全是可以使得每一帧做到足够小的，尽管从big O的意义上讲，这两种策略所对应的每一帧都可以认为是常数，但是这种常数的差异实际上是非常巨大的。

因此作为树算法的一个重要基石，遍历算法非常有必要从递归形式改写为迭代形式，同时经过这样的改写之后，我们也可以对整个遍历算法的过程以及原理获得更加深刻的认识。稍加观察不难发现此处的两句递归调用都非常类似于尾递归，其特征是递归调用出现在整个递归实例体的尾部，这种递归是非常容易化解为迭代形式的，为此我们只需引入一个栈。

1.2.迭代（版本1）

改写之后的第一个跌打版本，如这段代码所示，作为初始化取一个栈s用以存放树节点的位置，即它们的引用。首先将当前的树根x推入栈中，以下进入一个主体的循环，每一次弹出当前的节点并且随即对它进行访问，此后如果当前这个节点拥有右孩子就将右孩子推入栈中，如果有左孩子 那么左孩子也会随后入栈，此后整个循环又进入下一步迭代直到整个栈变空。

template <typename T, typename VST> //元素类型、操作器
void travPre_I1(BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法（迭代版#1）
	Stack<BinNodePosi(T)> S; //辅助栈
	if (x) S.push(x); //根节点入栈
	while (!S.empty()) { //在栈变空之前反复循环
		x = S.pop(); visit(x->data); //弹出并访问当前节点，其非空孩子的入栈次序为先右后左
		if (HasRChild(*x)) S.push(x->rc); if (HasLChild(*x)) S.push(x->lc);
	}
}

需要注意的是：左右孩子的入栈次序是先右后左，这是因为包括先序遍历在内的所有遍历，都先遍历左子树再去遍历右子树，在这个算法模式中既然每个节点都是在被弹出栈的时刻才接受访问，所以根据栈后进先出的特性，自然应该将希望后出栈的右子树先入栈了。

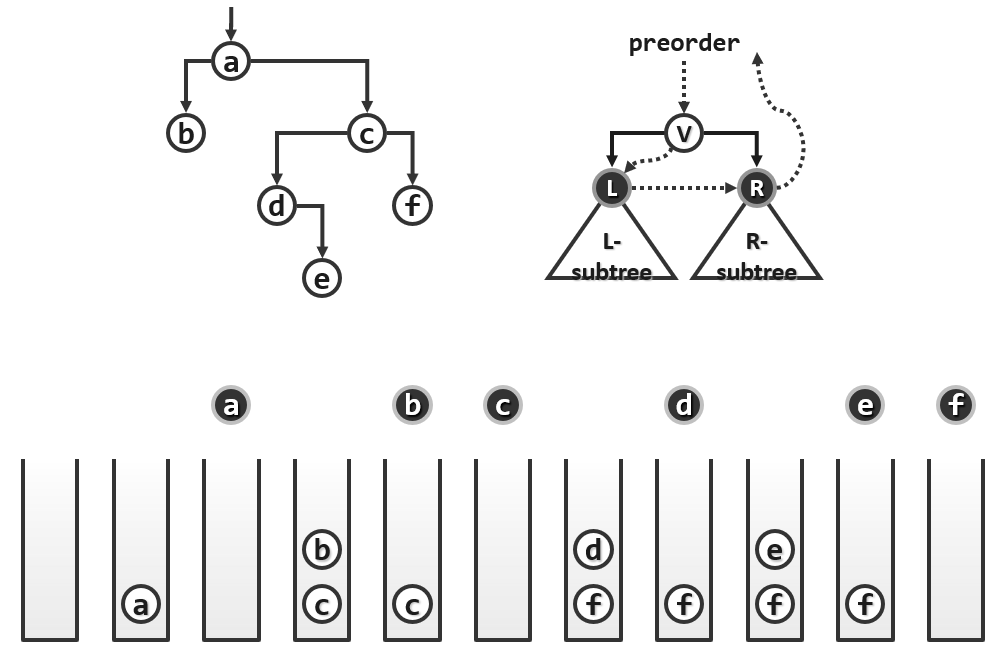
下面是一个实例：

• 正确性：

  • 无遗落：每个节点都会被访问到

    归纳假设：若深度为d的节点都能被正确访问到，则深度为d+1的也是

  • 根先：对于任一子树，根被访问后才会访问其他节点

    只需注意到：若u是v的真祖先，则u必先于v被访问到

  • 左先右后：同一节点的左子树，限于右子树被访问

• 效率：$O(n)$

  • 每步迭代，都有一个节点出栈并被访问；
  • 每个节点入/出栈一次仅且一次；
  • 每步迭代只需$O(1)$时间。

可以看到算法所输出的节点序列恰好就是我们所希望得到的先序遍历序列，第一个迭代版算法非常简明，然而遗憾的是这种算法策略并不容易直接推广到此后要研究的中序遍历和后序遍历算法，因此我们或许应该另辟蹊径寻找其它等效的策略。

1.3.迭代（版本2）

不妨从一个规模略大同时更具一般性的例子入手：

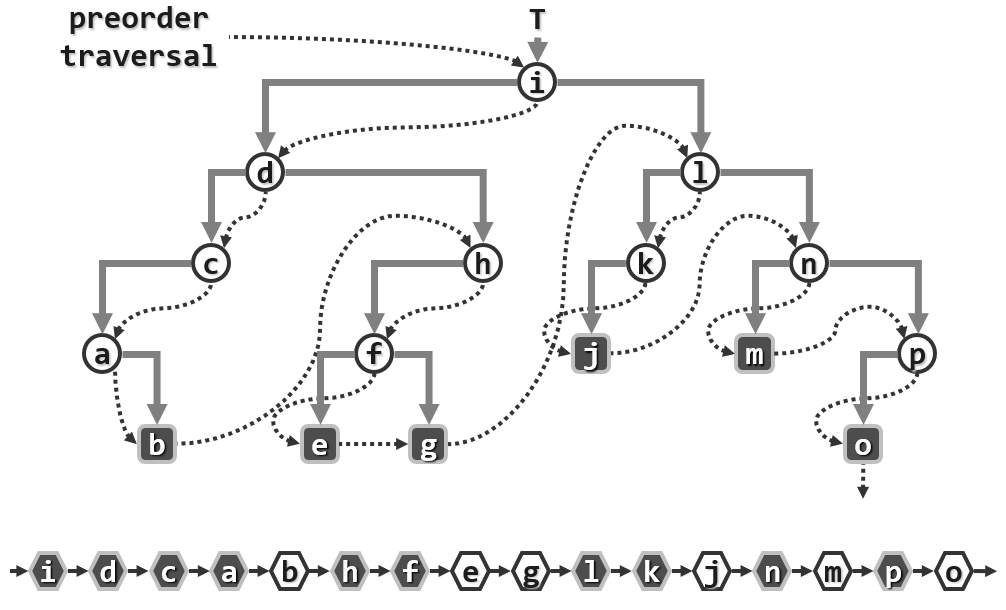
可以发现这样一个规律：一旦树根节点接过控制权并接受访问，接下来被访问的就是它的左孩子以及左孩子的左孩子，以及同样地，当不能下去的时候才会进行一次新的转移，而每转移到一个具体的局部，做的事情都是尝试着沿着这样的一个左孩子的分支不断地下行。

对于任何一棵子树，都将起始于树根的接下来总是沿着左侧孩子分支不断下行的这样一条链称作是当前这棵子树的左侧链，而这个算法就是沿着这个左侧链逐渐展开。

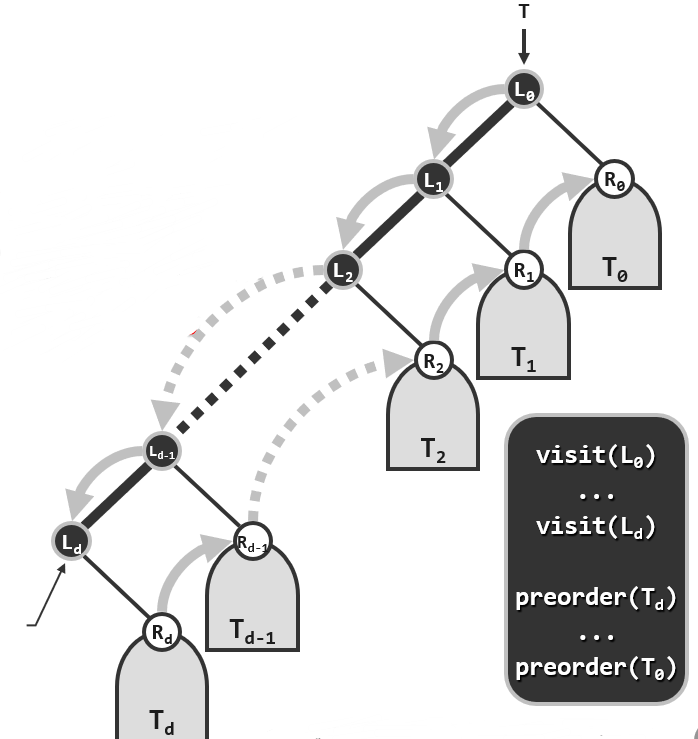
• 沿着左侧分支：各节点与其右孩子（可能为空）一一对应；
• 从宏观上，整个遍历过程可划分为：自上而下对左侧分支的访问，及随后自下而上对一系列右子树的遍历；
• 不同右子树的遍历相互独立，自成一个子任务。

新版本的迭代算符首先需要实现一个标准的例程visitAlongLeftBranch，它的任务就是来实现从根节点开始沿着left branch 不断下行，依次访问沿途所有节点的这样一个过程。

这个主算法则是反复地在每一个局部调用visitAlongLeftBranch这个例程来实现。

//从当前节点出发，沿左分支不断深入，直至没有左分支的节点；沿途节点遇到后立即访问
template <typename T, typename VST> //元素类型、操作器
static void visitAlongVine(BinNodePosi(T) x, VST& visit, Stack<BinNodePosi(T)>& S) {
	while (x) {
		visit(x->data); //访问当前节点
		S.push(x->rc); //右孩子入栈暂存（可优化：通过判断，避免空的右孩子入栈）
		x = x->lc;  //沿左分支深入一层
	}
}

template <typename T, typename VST> //元素类型、操作器
void travPre_I2(BinNodePosi(T) x, VST& visit) { //二叉树先序遍历算法（迭代版#2）
	Stack<BinNodePosi(T)> S; //辅助栈
	while (true) {
		visitAlongVine(x, visit, S); //从当前节点出发，逐批访问
		if (S.empty()) break; //直到栈空
		x = S.pop(); //弹出下一子树的树根
	}  #pop = #push = #visit = O(n) = 分摊O(1)
}

这里之所以使用一个栈而不是队列的用意，依然是因为栈的后进先出的特性，对于左侧链的访问的是自上而下的，存入栈中的右子树也就是自上而下的，而接着对右子树的遍历是自下而上的，对栈来说就是自顶向底的，对栈的一系列依次的pop操作则恰好可以实现栈中右子树的自顶向底的访问。

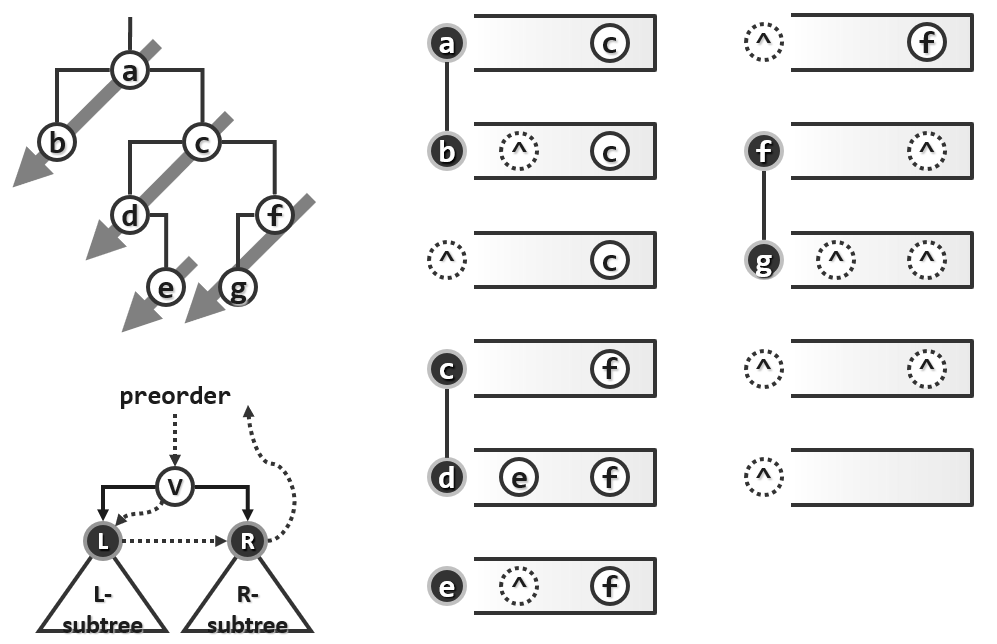
下面看一个实例：（^代表空）

2.中序遍历

2.1.递归

template <typename T, typename VST> //元素类型、操作器
void travIn_R(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（递归版）
	if (!x) return;
	travIn_R(x->lc, visit);
	visit(x->data);
	travIn_R(x->rc, visit);
}

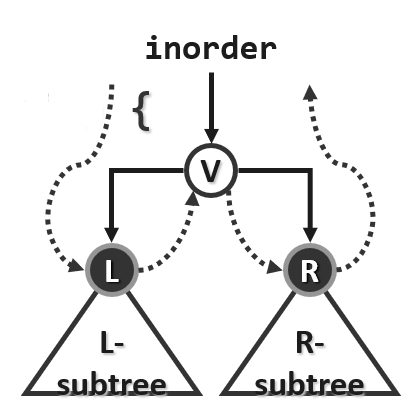
将递归转换为迭代的难点在于尽管右子树的递归遍历是尾递归，但左子树却严格地不是。解决方法可是是：找到第一个被访问的节点，将其祖先用栈保存，这样原问题就分解为依次对若干棵子树的遍历问题。

2.2迭代

同样从一个规模略大同时更具一般性的例子入手：

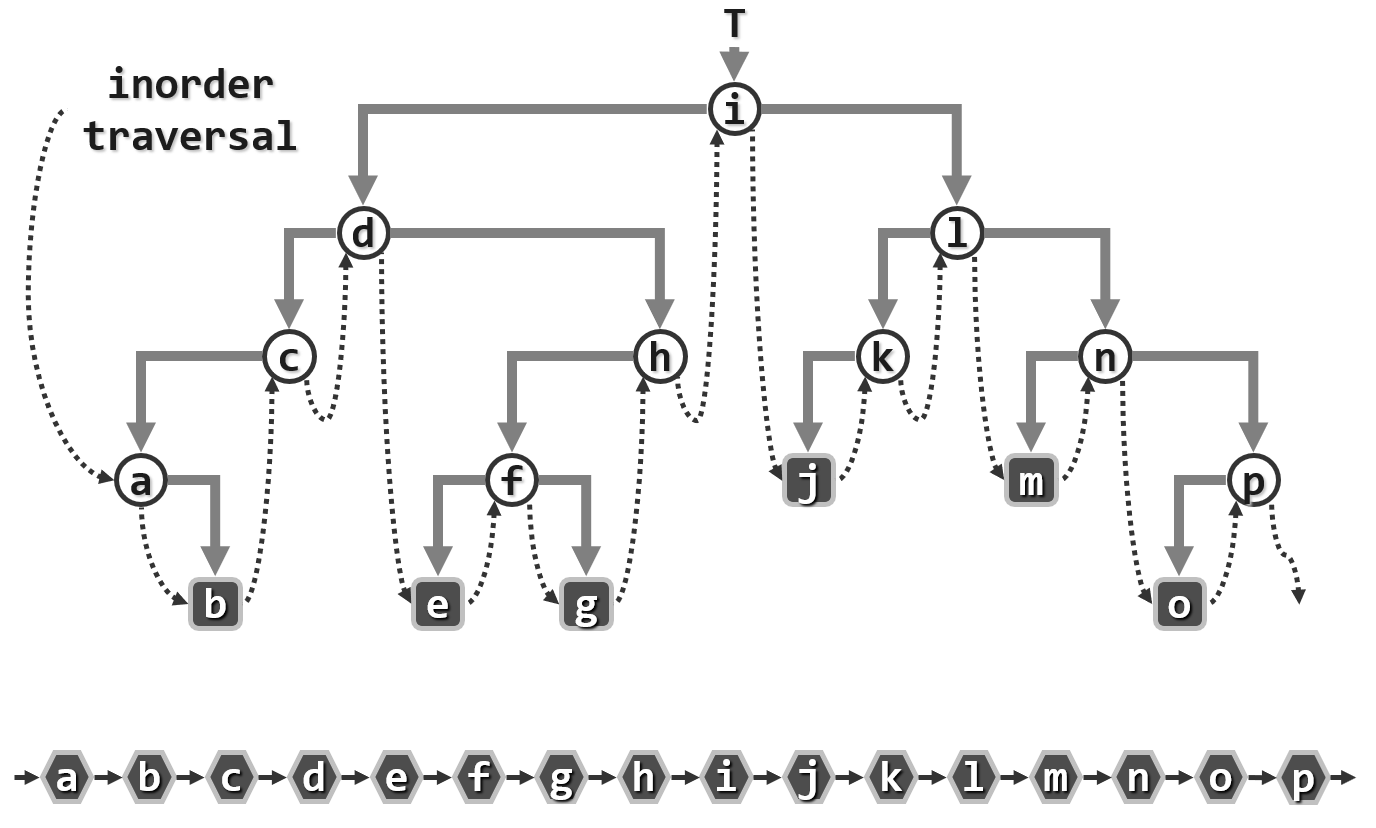
与先序遍历非常类似，整个中序遍历过程是从根节点开始，一直沿着左侧分支逐层向下，直到末端不能再向下的那个节点，因此可以将整个中序遍历分解为在不同尺度下的一系列的对左侧分支的逐步处理。我们可以将任何一棵二叉树抽象地规范为如下图所示的形式，整棵树可以分解为一条起自根节点的左侧链以及左侧链上各节点所对应的右孩子。

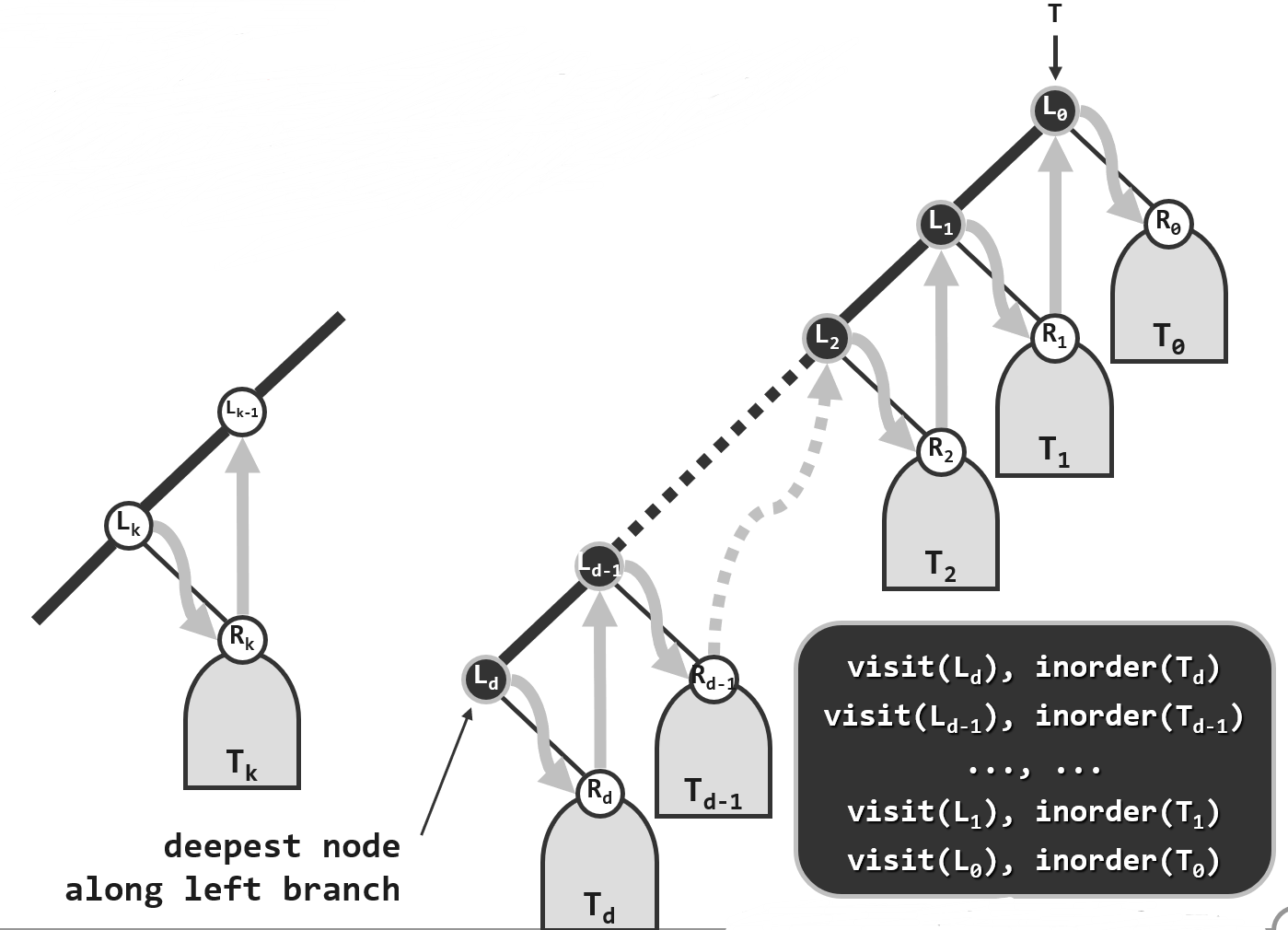
在一个局部，当前节点$L_{d-1}$将控制权交给并访问它的左孩子$L_d$后，再遍历$L_d$的右子树$T_d$，然后回到并访问节点$L_{d-1}$，再遍历其右子树$T_{d-1}$，如此反复直到遍历全树。在这样的一个过程中存在着某种逆序性，我们最初的起点是在根节点处可是首先接受访问的却是它所对应的左侧链的末端节点，如果说这个的过程是自顶而下的话，那么各节点实际被访问的次序大体而言是呈一种自下而上的过程，因此仍然要使用栈结构来实现这一过程。

template <typename T> //从当前节点出发，沿左分支不断深入，直至没有左分支的节点
static void goAlongLeftBranch(BinNodePosi(T) x, Stack<BinNodePosi(T)>& S) {
	while (x) { S.push(x); x = x->lChild; } //当前节点入栈后随即向左侧分支深入，迭代直到无左孩子
}

template <typename T, typename VST> //元素类型、操作器
void travIn_I1(BinNodePosi(T) x, VST& visit) { //二叉树中序遍历算法（迭代版#1）
	Stack<BinNodePosi(T)> S; //辅助栈
	while (true) {
		goAlongLeftBranch(x, S); //从当前节点出发，逐批入栈
		if (S.empty()) break; //直至所有节点处理完毕
		x = S.pop();     //x的左子树或为空，或已遍历（等效于空），故可以
		visit(x->data);  //弹出栈顶节点并访问之
		x = x->rChild;   //转向右子树
	}
}

下面是一个实例：

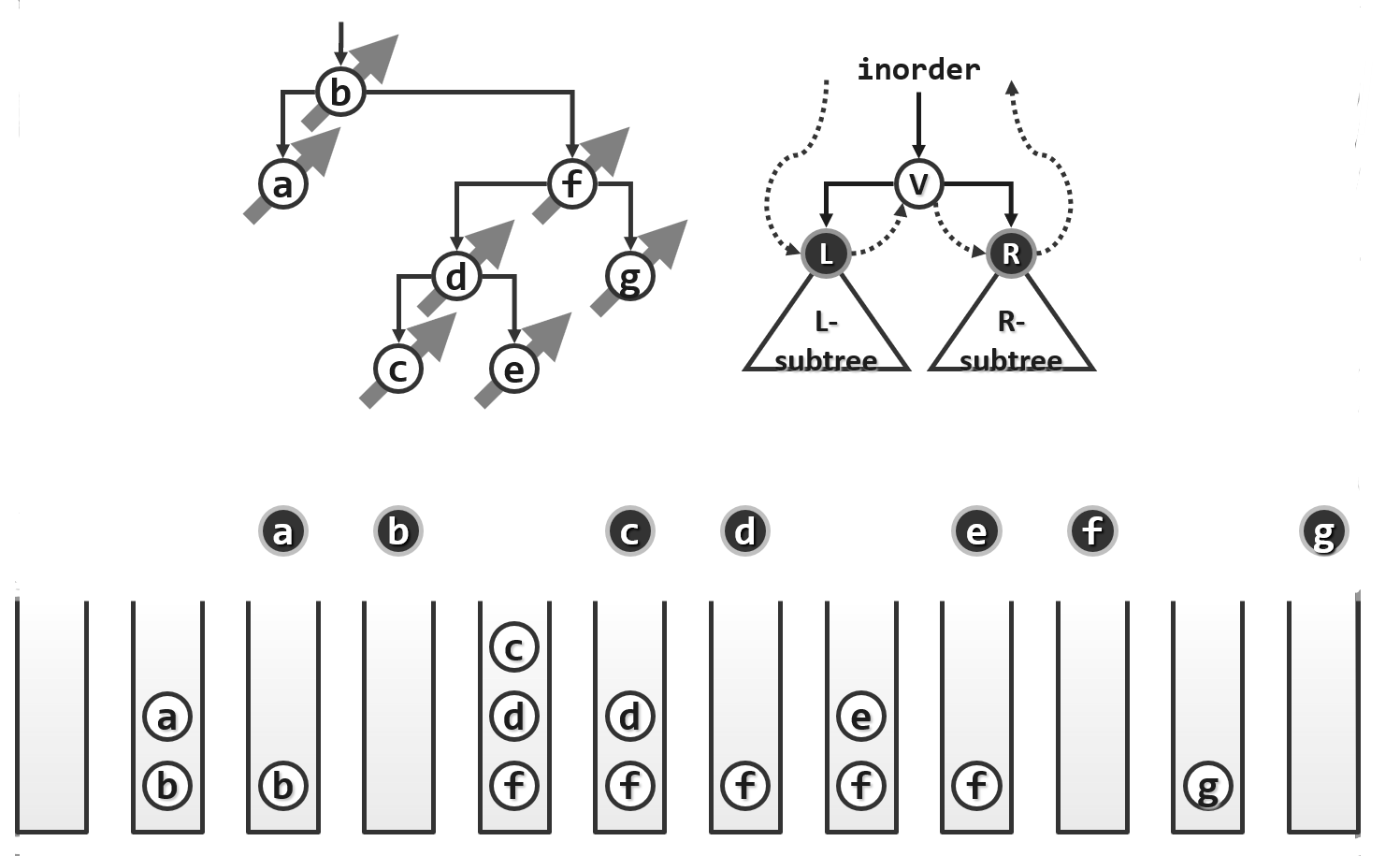
我们知道递归的版本可以简明地实现$O(n)$的复杂度，尽管它的常系数非常之大，那么迭代版本的时间复杂度仍是$O(n)$，但常系数要小的多（分摊分析）。尽管单次调用goAlongLeftBranch就可能需要做$\Omega(n)$次入栈操作需要$\Omega(n)$时间，但这些左侧链的长度加起来也不过是n，因此迭代算法的复杂度仍是线性的，即$O(n)$。

此外还要其他版本的中序遍历的迭代实现，如版本2：

template <typename T, typename VST> //元素类型、操作器
void travIn_I2 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#2）
   Stack<BinNodePosi(T)> S; //辅助栈
   while ( true )
      if ( x ) {
         S.push ( x ); //根节点进栈
         x = x->lc; //深入遍历左子树
      } else if ( !S.empty() ) {
         x = S.pop(); //尚未访问的最低祖先节点退栈
         visit ( x->data ); //访问该祖先节点
         x = x->rc; //遍历祖先的右子树
      } else
         break; //遍历完成
}

版本3：

template <typename T, typename VST> //元素类型、操作器
void travIn_I3 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历算法（迭代版#3，无需辅助栈）
   bool backtrack = false; //前一步是否刚从左子树回溯——省去栈，仅O(1)辅助空间
   while ( true )
      if ( !backtrack && HasLChild ( *x ) ) //若有左子树且不是刚刚回溯，则
         x = x->lc; //深入遍历左子树
      else { //否则——无左子树或刚刚回溯（相当于无左子树）
         visit ( x->data ); //访问该节点
         if ( HasRChild ( *x ) ) { //若其右子树非空，则
            x = x->rc; //深入右子树继续遍历
            backtrack = false; //并关闭回溯标志
         } else { //若右子树空，则
            if ( ! ( x = x->succ() ) ) break; //回溯（含抵达末节点时的退出返回）
            backtrack = true; //并设置回溯标志
         }
      }
}

版本4：

template <typename T, typename VST> //元素类型、操作器
void travIn_I4 ( BinNodePosi(T) x, VST& visit ) { //二叉树中序遍历（迭代版#4，无需栈或标志位）
   while ( true )
      if ( HasLChild ( *x ) ) //若有左子树，则
         x = x->lc; //深入遍历左子树
      else { //否则
         visit ( x->data ); //访问当前节点，并
         while ( !HasRChild ( *x ) ) //不断地在无右分支处
            if ( ! ( x = x->succ() ) ) return; //回溯至直接后继（在没有后继的末节点处，直接退出）
            else visit ( x->data ); //访问新的当前节点
         x = x->rc; //（直至有右分支处）转向非空的右子树
      }
}

3.层次遍历

我们此前讨论的有根有序树，任何一棵二叉树都被指定了一个特殊的节点：根节点，由此就可以在垂直方向按照深度将所有节点划分为若干个等价类，因此可以认为所谓的有根性对应的就是垂直方向的次序。

进一步地位于同一深度也属于同一等价类内部的所有节点，即所有的同辈节点也可以分出次序，比如对于二叉树可以通过左右的明确定义给出同辈节点之间的相对次序，因此可以认为有序给出沿水平方向的一个次序。

因此按照垂直方向和水平方向的次序可以在所有的节点之间定义一个整体的次序，并进而对它进行遍历。自高向低而在每一层自左向右逐一地访问树中的每一个节点的遍历策略及过程就是层次遍历。

此前的三种遍历策略：先序、中序和后序都无法保证所有节点严格地按照深度次序访问，都有后代限于祖先被访问的情况，即逆序，为此需要借助栈结构。反过来，在层次遍历中，所有节点的访问都满足顺序性，因此这里就需要借助与栈结构对称的队列结构。

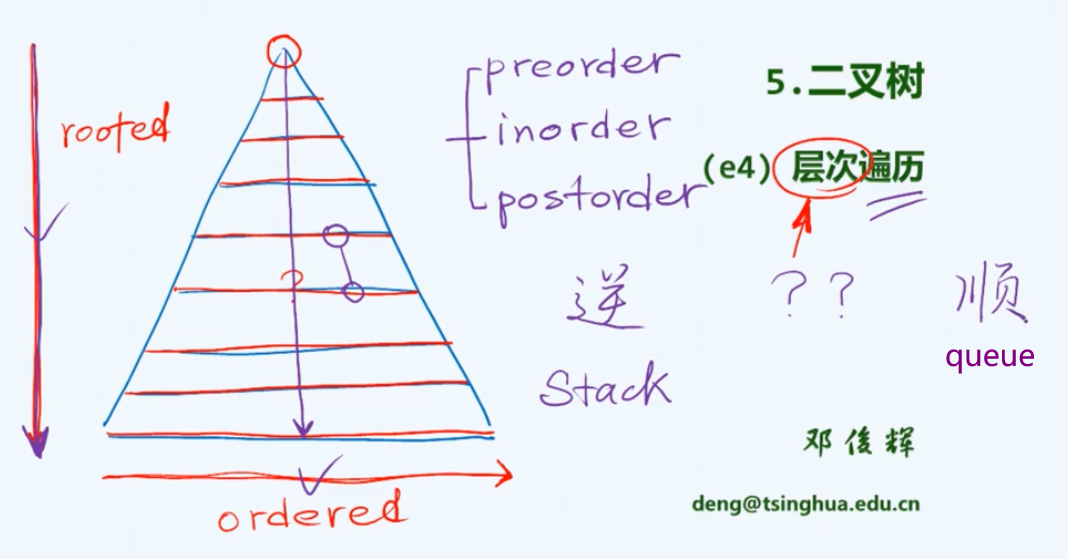
具体实现为：

template <typename T> template <typename VST> //元素类型、操作器
void BinNode<T>::travLevel ( VST& visit ) { //二叉树层次遍历算法
   Queue<BinNodePosi(T)> Q; //辅助队列
   Q.enqueue ( this ); //根节点入队
   while ( !Q.empty() ) { //在队列再次变空之前，反复迭代
      BinNodePosi(T) x = Q.dequeue(); visit ( x->data ); //取出队首节点并访问之
      if ( HasLChild ( *x ) ) Q.enqueue ( x->lChild ); //左孩子入队
      if ( HasRChild ( *x ) ) Q.enqueue ( x->rChild ); //右孩子入队
   }
}

下面是一个实例：

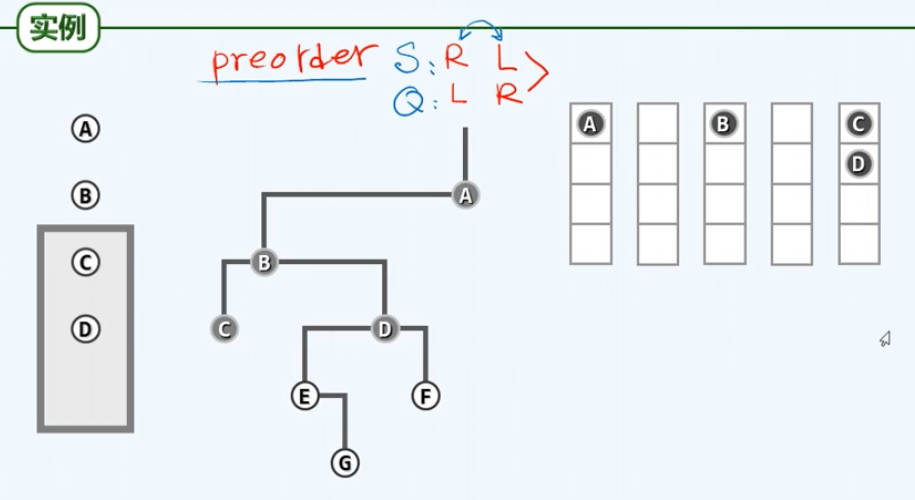
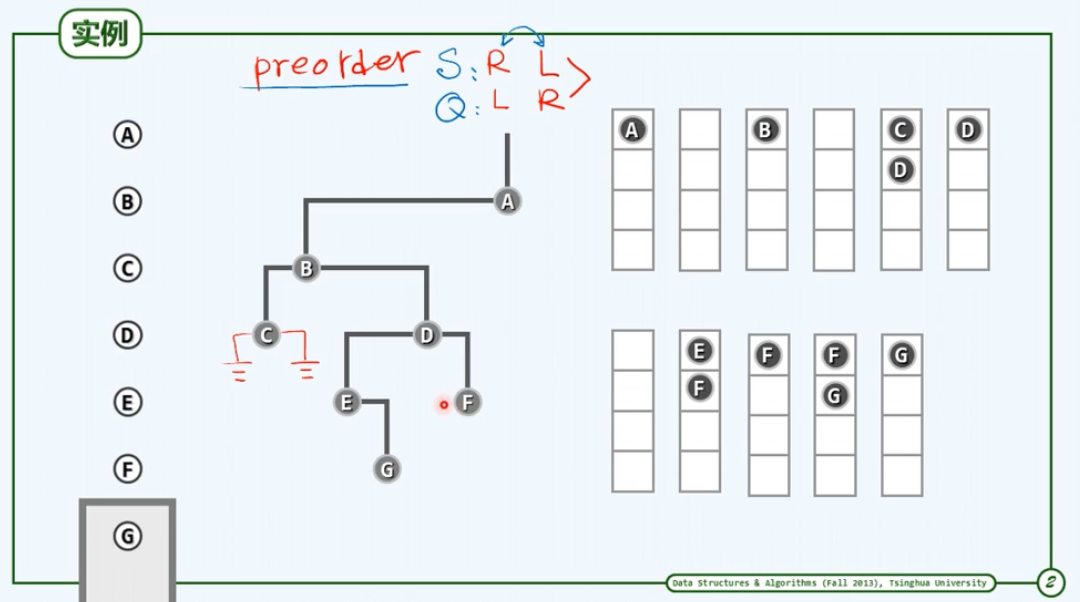
4.重构

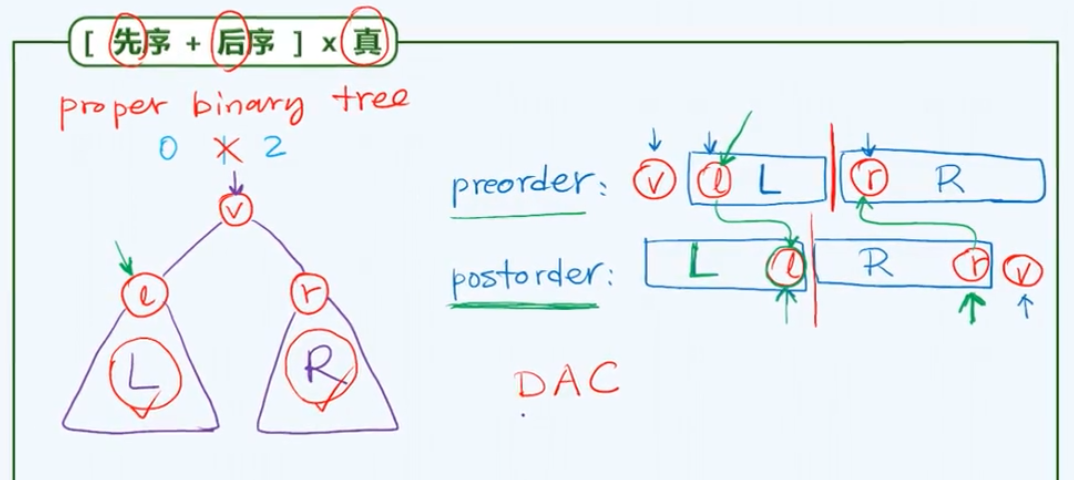
由任何一棵二叉树我们都可以导出三个序列：先序(preorder)、中序(inorder)和后序(postorder)遍历序列，这三个序列的长度相同，它们都是由树中的所有节点依照对应的遍历策略所确定的次序依次排列而成。那么如果我们已知某棵树的遍历序列，是否可以还原出这棵树的拓扑结构？什么情况下可以？什么情况下不可以？如果可以具体又应该使用什么样的方法？

关于二叉树重构的第一个结论是：只需中序遍历序列再加上先序与后序遍历序列之一，即可还原二叉树的完整拓扑结构。

用数学归纳来证明：假设对于规模小于大N的所有二叉树这个规律都是成立的，接下来考察规模恰好为N的二叉树。在先序遍历序列中可以地将左子树和右子树所对应的遍历子序列切分开。这样就将原来全树的重构问题化解为两棵子树的重构问题，这两棵子树在规模上都符合归纳假设，即它们都严格地小于大N，因此根据归纳假设无论是左子树还是右子树都可以重构出来。

当然你应该不难写出一个递归式的重构算法，需要特别注意的是无论是左子树还是右子树，都有可能是空树，在这种情况下树的规模应该是零。而不借助中序遍历序列而只凭借先序和后序遍历序列，是不能保证完成对左右子树的正确切分的。因为无论是L还是R都有可能是空树，在先序遍历或者后序遍历的表达中会出现歧义，我们无法根据先序遍历序列以及后序遍历序列来区分在这种情况下除去根节点之后的部分究竟是左子树还是右子树。

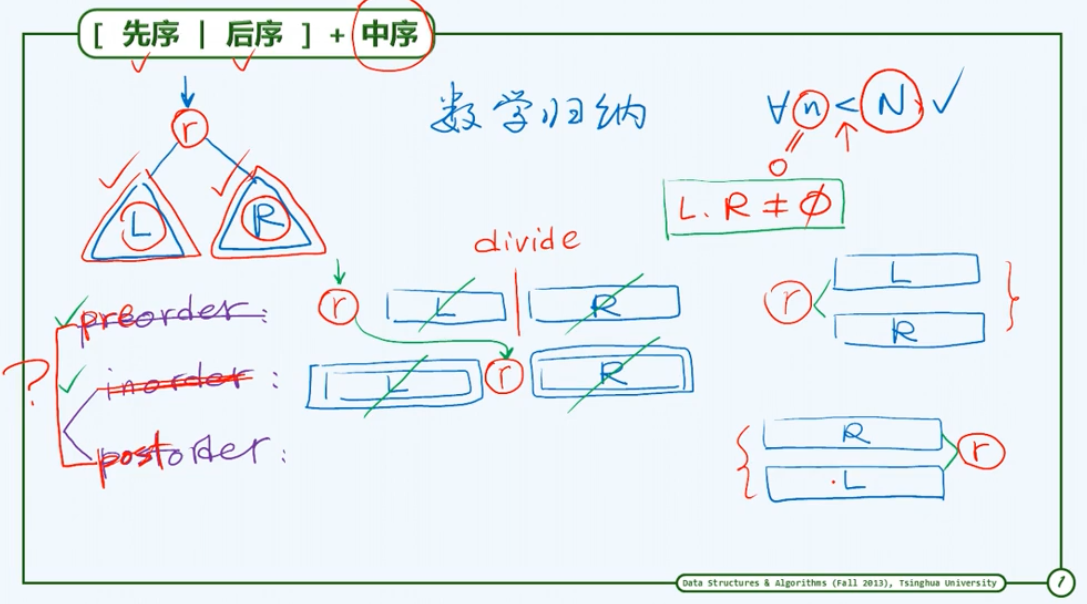
在某些特定情况下由先序和后序遍历序列也可以还原树的整体结构。比如对于真二叉树，每个节点的度数都必须是偶数，即0度或2度，此时的左子树和右子树要么同时为空要么同时非空。

在任何给定的先序遍历序列中都可以找到其左子树L，进而在后序遍历序列中对它进行定位，而这个节点在它所属的这棵子树的后序遍历子序列中必然垫后，这就意味着我们可以明确地界定左右子树的范围，即左子树由哪些节点构成以及右子树由哪些节点构成都是可以确定的。

当然对称地在后序遍历序列中，右子树的树根位置也是确定的，因此通过右子树的树根节点依然可以反过来在先序遍历序列中进行定位，而且同样地可以确定左右子树的切分位置。也就是说我们在这里
确实可以进行分而治之从而通过递归的形式，完整地重构出一棵真二叉树原本的结构。