1.广度优先搜索

1.1.算法

始自顶点s的广度优先搜索（Breadth-First-Search）
- 访问顶点s
- 依次访问s所有尚未访问的邻接顶点
- 依次访问它们尚未访问的邻接顶点
- …….如此反复，直至没有尚未访问的邻接顶点

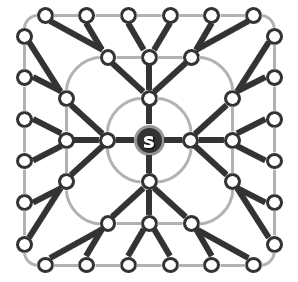
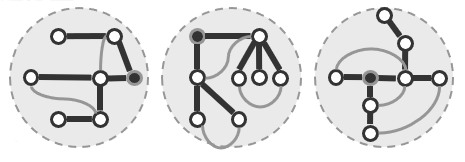
这种搜索将首先访问s，在这个图中通过将s染黑表示它已经接受了访问。接下来需要访问S所有尚未访问的邻接顶点，由s通往它的那些刚被访问的邻居的边都被加粗，这暗示着这些边都已经被算法所采纳和保留，这些边都是非常重要的，它们携带了整个遍历过程中所发现的一些信息。反过来在原图中还会有一些边并不采纳（浅色线部分）在经过广度优先遍历之后，它们将不再保留而是被舍弃掉。

这个算法将不断地如此迭代反复，直到所有的顶点都接受了访问。所谓广度优先搜索的确是一种遍历，它会按照刚才所介绍的策略确定不同顶点接受访问的次序，并且按照这种次序对各顶点逐个地访问，而整个搜索过程的最终产物或成果不过是选自原图的一系列的加粗的边。

这里按照与起点s的距离将所有的顶点划分为若干个等价类，在同一等价类内部各顶点的边都不会被采纳，而只有连接于相邻等价类之间的某些边才会被采纳。所有被保留下来并且采纳的这些边将足以把所有的顶点连接起来构成一个连通图，且它是一个极大无环图。这就相当于一棵树，这棵树中涵盖了原图的所有的顶点，所以称之为支撑树（Spanning Tree）。对于树而言，以上策略及过程完全等同于层次遍历。

1.2.实现

上述的策略可以实现而这样一段代码：

template <typename Tv, typename Te> //广度优先搜索BFS算法（单个连通域）
void Graph<Tv, Te>::BFS ( int v, int& clock ) { //assert: 0 <= v < n
   Queue<int> Q; //引入辅助队列
   status ( v ) = DISCOVERED; Q.enqueue ( v ); //初始化起点
   while ( !Q.empty() ) { //在Q变空之前，不断
      int v = Q.dequeue(); 
	  dTime ( v ) = ++clock; //取出队首顶点v
      for ( int u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
         if ( UNDISCOVERED == status ( u ) ) { //若u尚未被发现，则
            status ( u ) = DISCOVERED; Q.enqueue ( u ); //发现该顶点
            status ( v, u ) = TREE; parent ( u ) = v; //引入树边拓展支撑树
         } 
         else { //若u已被发现，或者甚至已访问完毕，则
            status ( v, u ) = CROSS; //将(v, u)归类于跨边
         }
      status ( v ) = VISITED; //至此，当前顶点访问完毕
   }
}

可以看到遍历的起点总是某个预先指定的顶点v，既然图的广度优先遍历可以视作为树的层次遍历的一种推广，所以与后者相仿这里依然借助一个队列结构来实现。在v入队之前将它的状态由最初的undiscovered转化为discovered，接下来的while循环每次都通过dequeue()取出队首的顶点并且重新命名为v。

请注意在每一个顶点刚刚出队并随即接受访问的同时，我们还需要给它打上一个时间标签dTime，在算法的入口处还有一个名为clock的引用型参数，它就像是一块钟表在整个算法的运行过程中都会给出时间的进度，任何时候如果你希望加注当前的时间标签，只需要将这块表取出来并读取上面的时刻。

按照算法的策略我们需要枚举出当前节点v的所有邻居，通过for循环语句来实现，firstNbr以及nextNbr接口在上文有介绍过。

经过整个的遍历搜索过程，每一个顶点的状态都会由最初的undiscovered转化为discovered，并最终转化为visited，这样的三个状态也就构成了每一个顶点在它的生命期内的三部曲。

下面以一个无向图为例来理解算法的过程：

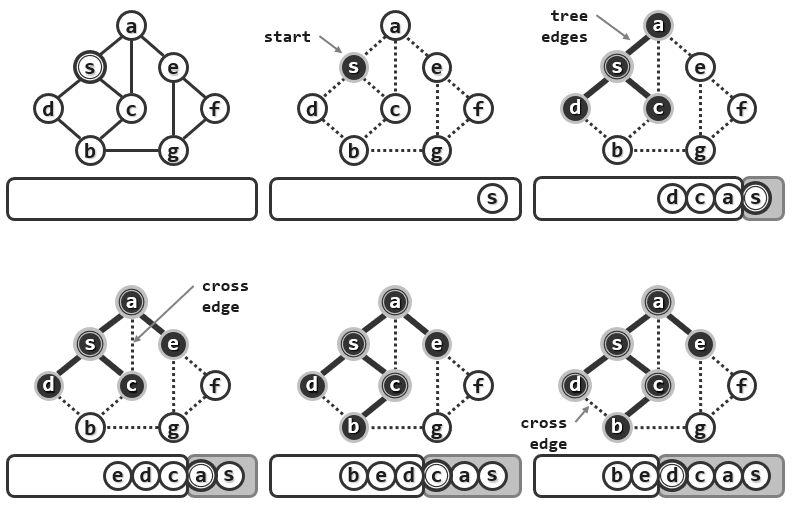
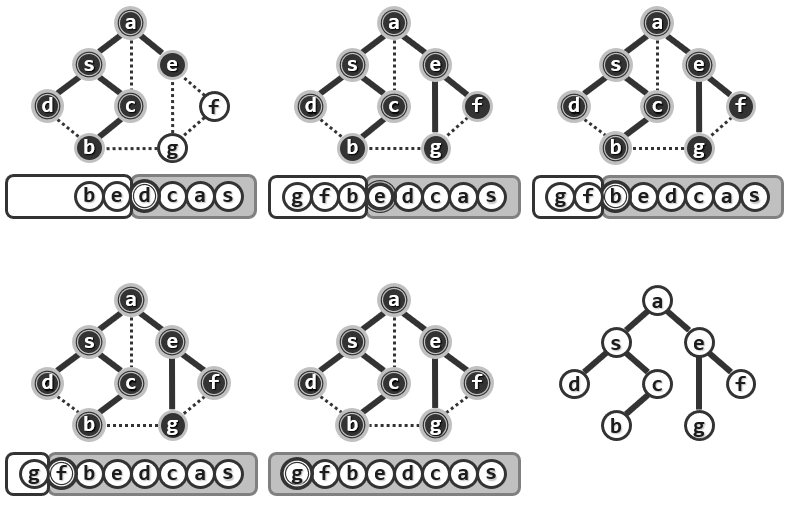
1.3.全图BFS

与起始顶点s相连通的每一个顶点都会被bfs搜索、发现并访问，即s顶点所属的那个连通域确实可以被悉数的遍历。然而问题是并非每幅图都只包含一个连通域，那么在含有多个连通域的时候从任何一个起点s出发未必能够抵达其它的连通域。那么这种情况如何处理，如何使得bfs搜索足以覆盖整幅图呢，可以采用下面的方法：

template <typename Tv, typename Te> //广度优先搜索BFS算法（全图）
void Graph<Tv, Te>::bfs ( int s ) { //assert: 0 <= s < n
   reset(); int clock = 0; int v = s; //初始化
   do //逐一检查所有顶点
      if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
         BFS ( v, clock ); //即从该顶点出发启动一次BFS
   while ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}

这里毕竟引入了一层新的循环而且至少从表面看来，这个循环的迭代次数将多达线性次。但这里并非对每一个顶点都启动一轮bfs搜索，而是只有在当前的顶点能够经过这个if判断（顶点尚未被发现）之后才启动这样一次搜索。这种处理方式可以保证对于每一个连通域只有一个顶点可能作为起点引起它所属的那个连通域被完全的遍历掉，每一个连通域启动而且只启动一次广度优先搜索，因此所有花费在搜索上的时间累计也不过是对全图的一次遍历，而不是多次。

1.4.复杂度

广度优先搜索算法的复杂度取决于不同实现方法，尤其是图结构自身的实现算法，这里不妨就以我们的实现版本为例，算法主体的复杂度部分是由while以及for所构成的两重循环。

1.5.最短路径

最好来讨论BFS算法的一个特性：最短距离性。

回顾此前所介绍的树结构，相对于树根节点任何一个节点v都对应于一条唯一的通路，这条路径的长度称作顶点v的深度depth(v)，于是我们可以对所有的顶点自上而下按照它们的深度进行等价类划分，在每一个等价类中的所有顶点所具有的深度指标都是彼此相等的。而树的层次遍历也可以认为是按照这一指标非降的次序，将所有的顶点逐一枚举出来。

那么这样一个遍历的过程是否也可以转化为图结构的遍历过程呢？表面看来似乎不太容易，因为此时与树结构极不相同的就是从起始顶点s出发可能有多条路径都最后通往同一个顶点，而且可能出现分叉。然而这样一个问题不难解决，实际上我们只需考察顶点之间的最短通路，并且将这两个顶点之间的距离取作这条最短通路的长度dist(v, s)。

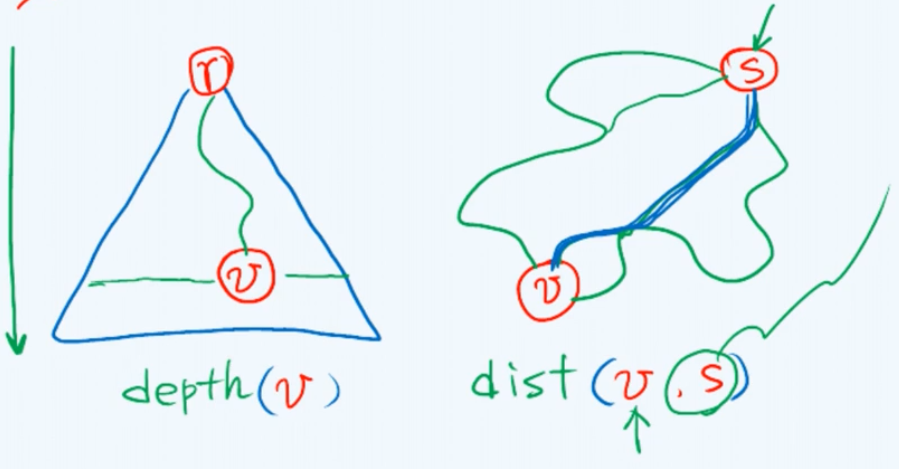
巧合的是图的BFS搜索与树的层次遍历一样都具有这样一种单调性，即BFS所给出的顶点序列按照这样到起点的距离也是按照非降次单调排列的。在我们最终所生成的BFS树中，每个顶点与s之间的那条通路恰好就是在原图中这两个顶点之间的最短通路。

2.深度优先搜索

2.1.算法

这一节将介绍与上一节中的广度优先搜索完全对称的另一种搜索算法：深度优先搜索。相对于此前的广度优先搜索，深度优先搜索的算法策略更为简明，然而深度优先搜索的过程更为复杂，其功能也相对而言更为强大，因此也成为有效解决很多实际问题的。

深度优先搜索的基本算法框架如下：

首先确定一个搜索的起点s，找到它的任意的一个邻居，并且将控制权交给这个新的顶点。接下来新的顶点一旦接过控制权，它也会仿效这种策略在它的所有邻居中任选其一，并且将控制权交给这个尚未访问的邻居。当然如果有已经被访问过的，对应的这条边将不会被采用，而是以某种适当的形式加以标注（图中以浅色线表示）。假设这个顶点已经没有任何邻居尚未访问，那么按照算法的策略，我们将在这个位置返回（回溯），顺着此前的通路回到它的前驱顶点。

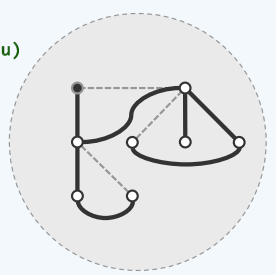
可以看到遍历的效果与此前的BFS类似，我们依然会得到一棵DFS树，也就是图中这些粗边所构成的一棵支撑树，同样地未被这棵树所采纳的那些边会被分类，而且这种分类要更为细致。

这样一个遍历和递归的过程可以实现为下面的代码：

template <typename Tv, typename Te> //深度优先搜索DFS算法（单个连通域）
void Graph<Tv, Te>::DFS ( int v, int& clock ) { //assert: 0 <= v < n
   dTime ( v ) = ++clock; status ( v ) = DISCOVERED; //发现当前顶点v
   for ( int u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
      switch ( status ( u ) ) { //并视其状态分别处理
         case UNDISCOVERED: //u尚未发现，意味着支撑树可在此拓展
            status ( v, u ) = TREE; parent ( u ) = v; DFS ( u, clock ); break;
         case DISCOVERED: //u已被发现但尚未访问完毕，应属被后代指向的祖先
            status ( v, u ) = BACKWARD; break;
         default: //u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边
            status ( v, u ) = ( dTime ( v ) < dTime ( u ) ) ? FORWARD : CROSS; break;
      }
   status ( v ) = VISITED; fTime ( v ) = ++clock; //至此，当前顶点v方告访问完毕
}

template <typename Tv, typename Te> //深度优先搜索DFS算法（全图）
void Graph<Tv, Te>::dfs ( int s ) { //assert: 0 <= s < n
   reset(); int clock = 0; int v = s; //初始化
   do //逐一检查所有顶点
      if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
         DFS ( v, clock ); //即从该顶点出发启动一次DFS
   while ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}

2.2.实例（无向图）

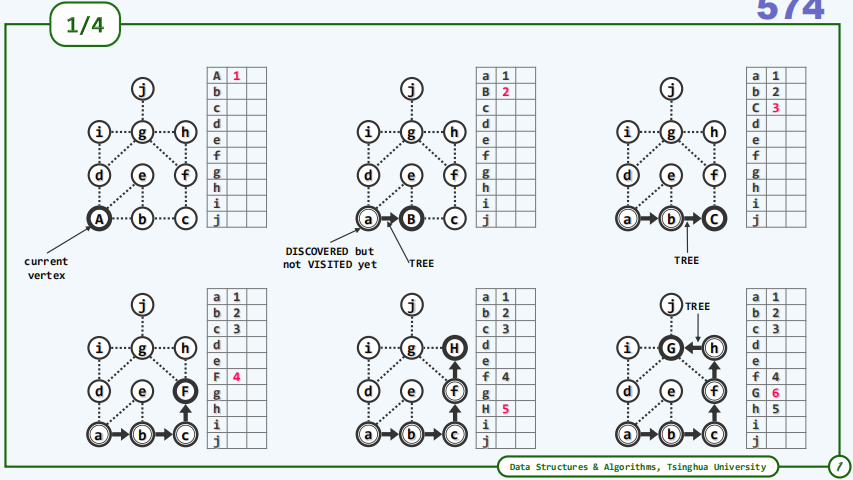
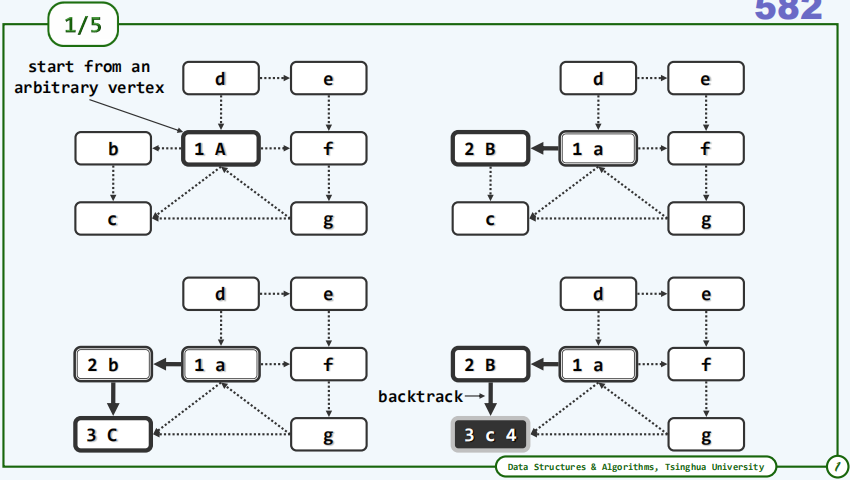
下面是一个无向图的实例，每一行的3格分别代表顶点及其dTime和fTime，为了方便理解将当前顶点在图中变为大写字母。

2.3.实例（有向图）

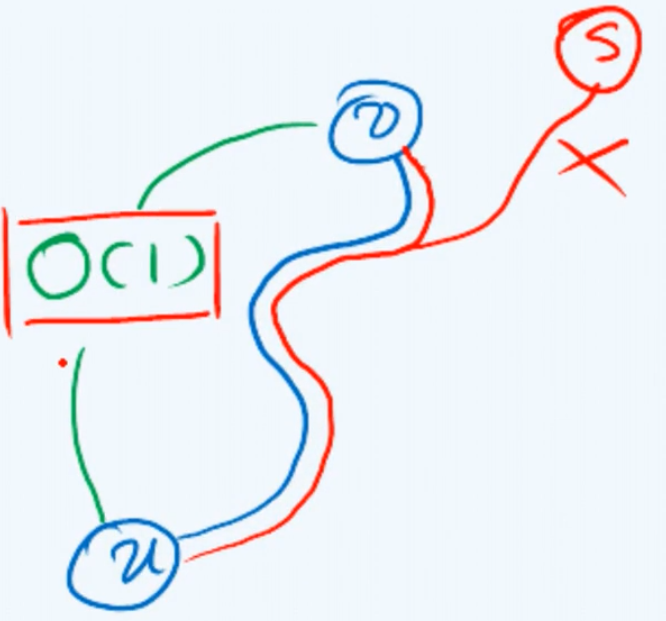
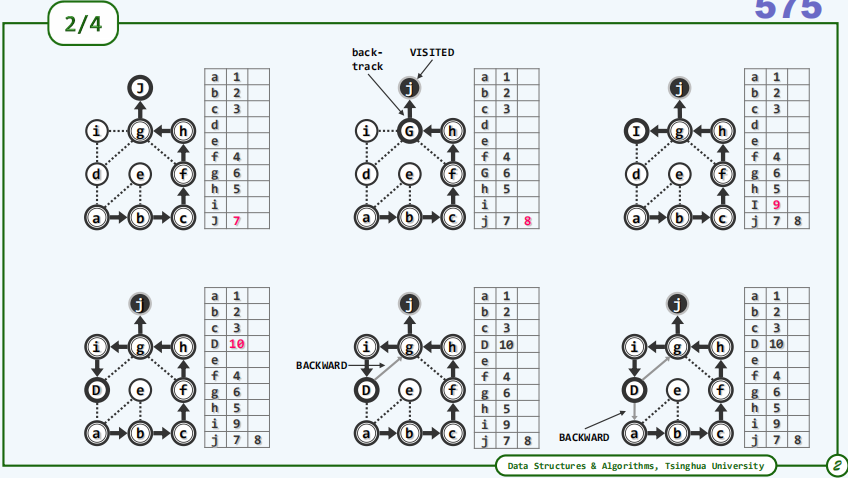
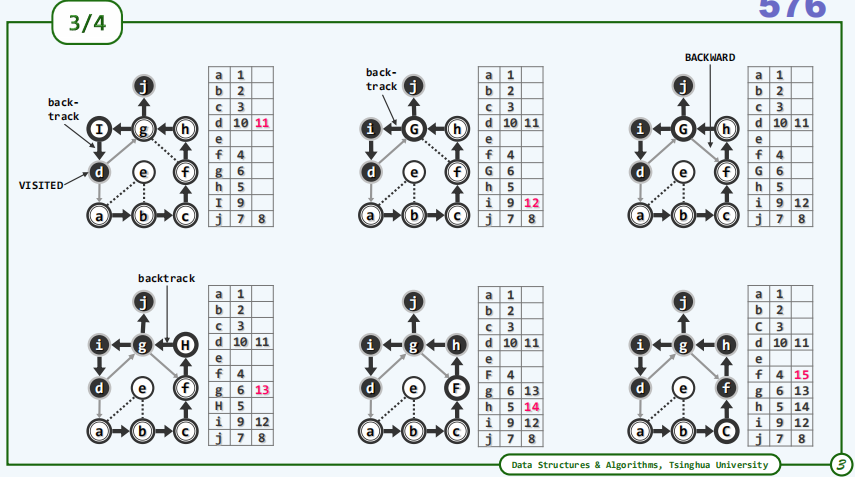
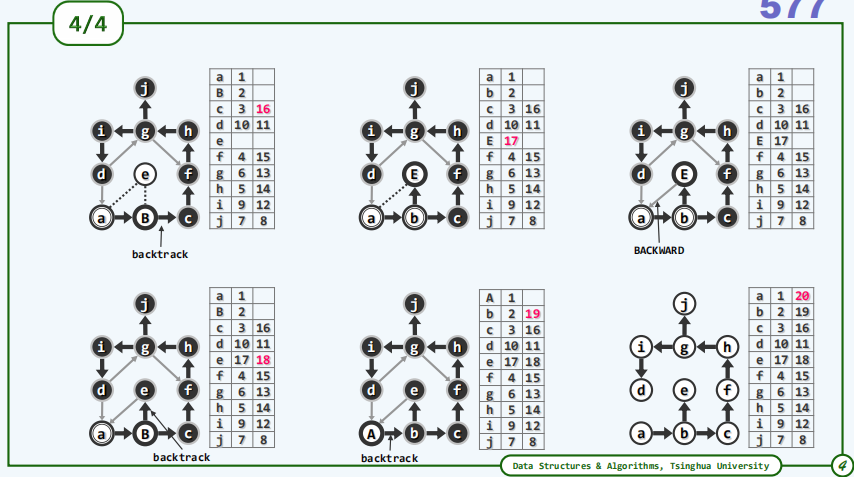
有向图的深度优先搜索要更为复杂，所涉及的情况也会更多。不妨来看下面的一个实例，首先确认这是一幅有向图，在这个图中我们将每一个顶点都绘制成长方形，顶点的标识居中，在它的左右空白处将分别记录下它在遍历过程中所获得的dTime和fTime两个时间标签。当前顶点用深色加粗边框表示且字母大写，被访问过的顶点用双线边框表示，处于VISITED状态的顶点用黑色方框表示。

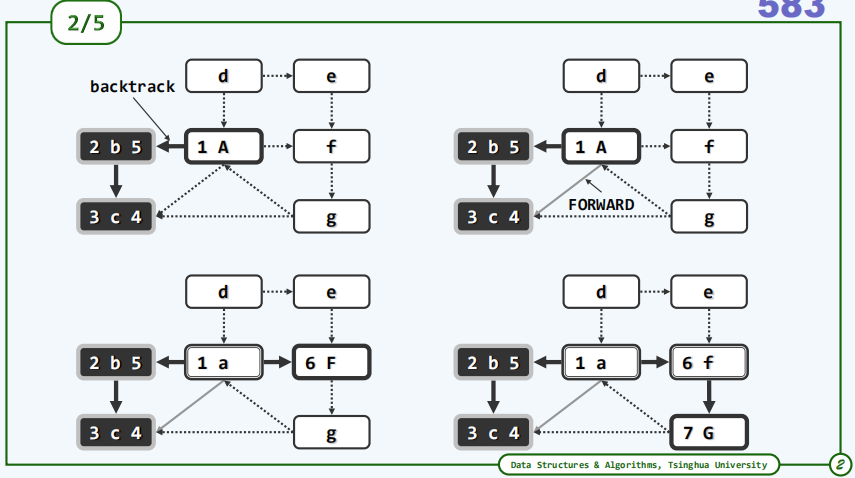
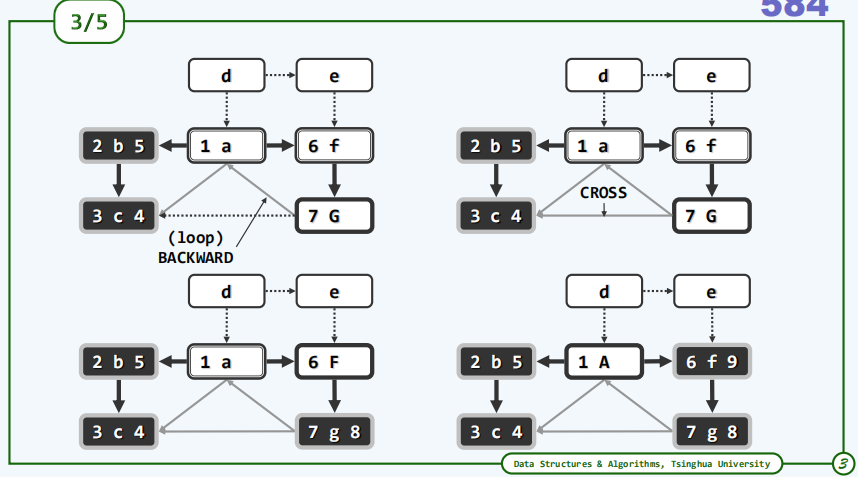
综观整个过程，我们总共用了10秒遍历完了由这五个顶点所构成的一个子图，更确切地讲它们构成了在这个图中从顶点a出发可以达到的区域，也称作可达区域。那么图中的其余部分呢？比如说这里的顶点d以及e呢？

回顾对广度优先遍历算法bfs的处理手法，就不难发现我们完全可以效仿那种做法，在这样的dfs算法之外再包装一层循环来枚举图中的所有顶点。这样的话就可以无一遗漏地遍历图中的所有顶点，而且只要处理得当对所有可达域的遍历都不会彼此有所重叠，从而在时间效率上也依然可以得到保证。

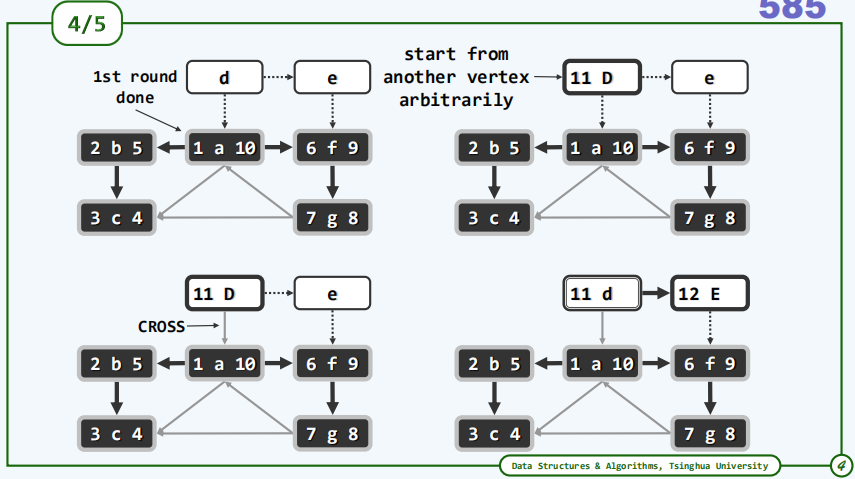
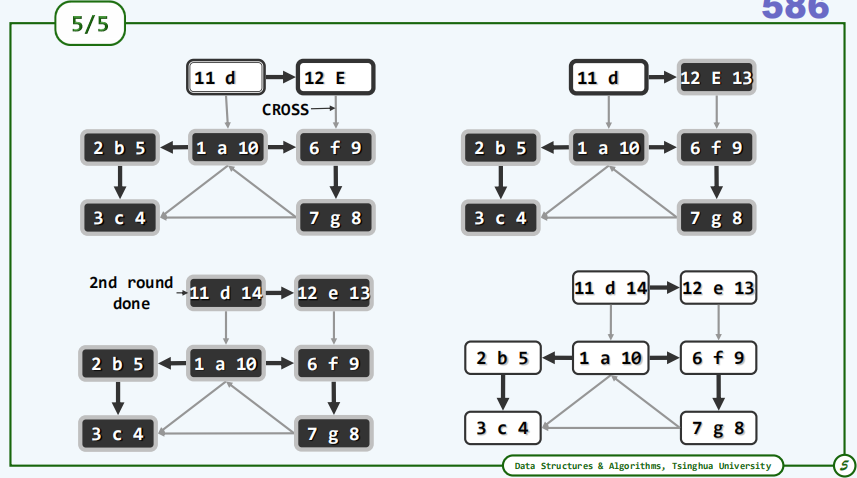
最后不妨来盘点一下遍历所获得的成果，首先是这些粗边它们构成了两棵遍历树，整体地构成了一个遍历森林；此外我们还对所有未被采纳的边进行了分类：跨越边、前向边以及后向边，无一遗漏。在通过遍历所获得的所有这些信息中遍历树或者说遍历森林无疑是最为重要的，然而相对于原图，它们毕竟只是一个子集，这样一个子集所携带的难道是原图的所有信息吗？从某种意义上讲的确是这样的，而其中至关重要的一点就在于我们通过遍历不仅获得了这样一棵树，而且为每一个顶点都标记了dTime和fTime两类时间标签，而这两类时间标签的作用是非常巨大的。

2.4.括号引理/嵌套引理

通过深度优先搜索DFS为图中所有顶点所标注的两个时间标签dTime和fTime，实际上蕴含了大量有用的信息这一点可以由括号引理或嵌套引理来加以印证。

为此首先要引入顶点的活动期的概念，也就是由它的dTime和fTime两个时间标签所界定的那样一段时间范围，即这个顶点在整个DFS搜索过程中处于活跃状态的时间范围。嵌套引理指出任何有向图经过了DFS搜索之后，在对应的DFS森林或者DFS树中任何一对顶点之间存在直系的血缘关系，当且仅当它们的活跃期存在包含与被包含的关系。

为了获得对这个引理更为直观的认识，我们不妨以横向作为时间轴，依然以上节的有向图为例，将每个顶点都沿水平方向适当展开使得它们恰好覆盖各自所对应的活跃期。不难看出祖先的活跃期的确会覆盖它的后代，而反过来没有直接血缘关系的节点比如说F和B，或者B和G，它们的活跃期都的确彼此没有任何公共的部分。

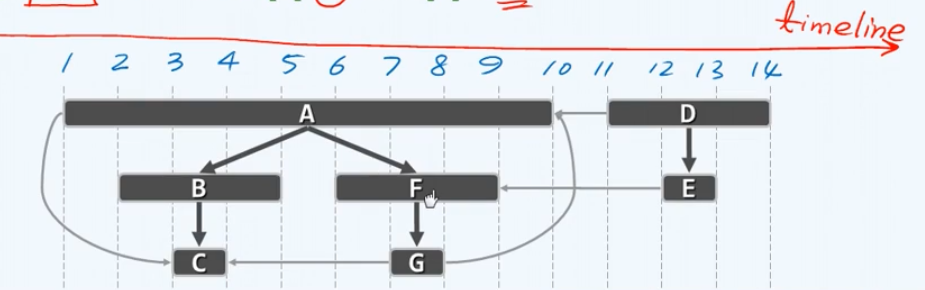
这样一种特性是非常强大的一个工具，比如在算法中我们经常需要做的一个判断就是：任意的一对顶点 v 和 u 之间在遍历树中是否存在一个直系血缘的关系。如果没有这样一种简便的机制，我们将不得不从 u 出发顺着parent引用不断地溯流而上直到遇到顶点v，才能够确定它们的确存在祖先和后代的直系关系；或者不得不一直追溯到整个遍历的起点，从而断定u和v之间并没有直系血缘关系。而现在借助时间标签，我们可以快速准确地在$O(1)$的时间内就得出相应的结论。