数据结构与算法（13）二叉搜索树

1.概述

回顾在第二，三章作为基础所介绍的两类基本数据结构：向量和列表，虽然它们都已经可以解决相当多的问题，然而对于进一步的算法设计要求来说它们都显得力不从心。基本的数据结构，可以在一定程度上支持静态查找但很遗憾，并不能高效地兼顾静态查找与动态修改。

在第五章我们做了改进的尝试，通过对一维列表的拓展引入了树结构或者说二叉树结构，二叉树结构可以认为是二维的列表，即列表在维度上的一种扩充。

而这一章要介绍的二叉搜索树（binary search tree，BST），它首先在形式上继承了二叉树也就是列表结构的特点，同时也巧妙地借鉴了向量，或者更准确地讲是有序向量的特点和优势。相对而言后一方面的借鉴更为重要，如果此前对列表结构的借鉴只是外表的形式，那么这种对有序向量特点的借鉴才是一种质的提高，这也是BST相对于其它的数据结构最为 “传神”的部分。实际上BST中所有这些传神的部分都集中体现在其中的一个子集：平衡二叉搜索树（balanced binary search tree，BBST），在接下来的两章中会介绍其中最具代表性的几个变种。

1.1.循关键码访问

二叉搜索树的数据项之间，按照各自的关键码彼此区分（call-by-key）。

前提条件是：关键码之间支持大小比较与相等比对。

因此为了简化和抽象不妨将整个数据集中的数据项都已统一地表示和实现为词条entry的形式：

template <typename K, typename V> struct Entry { //词条模板类
   K key; V value; //关键码、数值
   Entry ( K k = K(), V v = V() ) : key ( k ), value ( v ) {}; //默认构造函数
   Entry ( Entry<K, V> const& e ) : key ( e.key ), value ( e.value ) {}; //基于克隆的构造函数
   bool operator< ( Entry<K, V> const& e ) { return key <  e.key; }  //比较器：小于
   bool operator> ( Entry<K, V> const& e ) { return key >  e.key; }  //比较器：大于
   bool operator== ( Entry<K, V> const& e ) { return key == e.key; } //判等器：等于
   bool operator!= ( Entry<K, V> const& e ) { return key != e.key; } //判等器：不等于
}; //得益于比较器和判等器，从此往后，不必严格区分词条及其对应的关键码

若二叉树中各节点所对应的词条之间支持大小比较，则在不致歧义的情况下，我们可以不必严格区分树中的节点、节点对应的词条以及词条内部所存的关键码。

1.2.顺序性

在二叉搜索树BST中处处中都满足顺序性：

• 任一节点r的左子树中的所有节点都不大于r；

• 任一节点r的右子树中的所有节点都不小于r。

为回避边界情况，这里暂且假设所有节点互不相等，于是上述顺序性便可简化表达为：

• 任一节点r的左子树中的所有节点都小于r；
• 任一节点r的右子树中的所有节点都大于r。

当然在实际应用中，对相等元素的禁止既不自然也不必要。顺序性虽然只是对局部特征的刻画，但可由此导出某种全局特征：BST的中序遍历序列，必然单调非降。这一性质也是BST的充要条件，即任何一颗二叉树是二叉搜索树当且仅当中序遍历序列单调非降。（二叉树图中往下垂直投影就可以得到中序遍历序列）

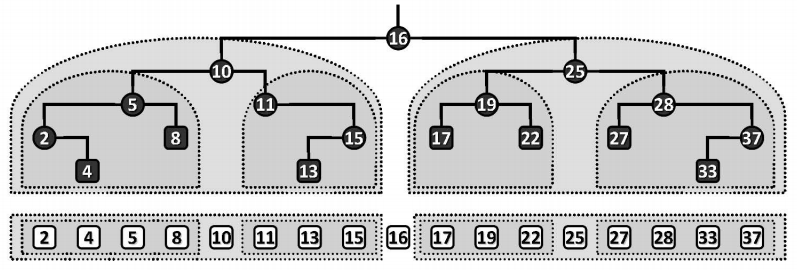
二叉搜索树属于二叉树的特例，故可以基于BinTree模板类派生出BST模板类：

#include "BinTree/BinTree.h" //引入BinTree

template <typename T> class BST : public BinTree<T> { //由BinTree派生BST模板类
protected:
   BinNodePosi(T) _hot; //“命中”节点的父亲
   BinNodePosi(T) connect34 ( //按照“3 + 4”结构，联接3个节点及四棵子树
      BinNodePosi(T), BinNodePosi(T), BinNodePosi(T),
      BinNodePosi(T), BinNodePosi(T), BinNodePosi(T), BinNodePosi(T) );
   BinNodePosi(T) rotateAt ( BinNodePosi(T) x ); //对x及其父亲、祖父做统一旋转调整
public: //基本接口：以virtual修饰，强制要求所有派生类（BST变种）根据各自的规则对其重写
   virtual BinNodePosi(T) & search ( const T& e ); //查找
   virtual BinNodePosi(T) insert ( const T& e ); //插入
   virtual bool remove ( const T& e ); //删除
   /*DSA*/
   /*DSA*/void stretchToLPath() { stretchByZag ( _root ); } //借助zag旋转，转化为左向单链
   /*DSA*/void stretchToRPath() { stretchByZig ( _root ); } //借助zig旋转，转化为右向单链
   /*DSA*/void stretch();
   /*DSA*/void imitate ( const BST<T> & ); //临摹
};

在继承原模板类BinTree的同时，BST内部也继续沿用了二叉树节点模板类BinNode。BST中新增了三个接口search()，insert()，和remove()，这三个标准接口的调用参数都是属于元素类型T的对象引用，这正是此类结构“循关键码访问”方式的具体体现。以BST为基类可以进一步派生出二叉搜索树的多个变种，因此这里的三个接口在前面加上virtual定义为虚函数。由于这些操作接口涉及词条的大小和相等的关系，因此这里假定基本元素类型T直接支持比较和判等操作，或者已重载过对应的操作符。

2.算法及实现

2.1. BST：查找

二叉搜索树的查找算法，亦采用了减而治之的思路与策略，其执行过程可描述为：从树根出发，逐步地缩小查找范围，知道发现目标（成功）或缩小至空树（失败）。

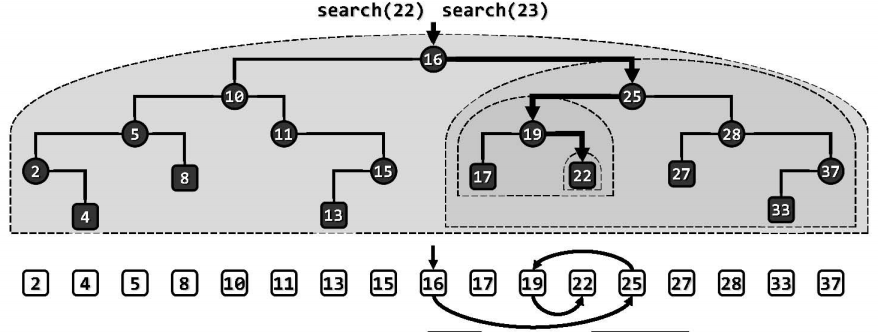
一般地，在上述查找过程中，一旦发现当前节点为NULL，即说明查找范围已经缩小至空，查找失败；否则，视关键码比较结果，向左（更小）或向右（更大）深入，或者报告成功。对照中序遍历序列可见，整个过程与有序向量的二分查找过程可视为等效。

BST的search()可以实现为下面一段代码：

template <typename T> BinNodePosi(T) & BST<T>::search ( const T& e ) //在BST中查找关键码e
{ return searchIn ( _root, e, _hot = NULL ); } //返回目标节点位置的引用，以便后续插入、删除操作

template <typename T> //在以v为根的（AVL、SPLAY、rbTree等）BST子树中查找关键码e
static BinNodePosi(T) & searchIn ( BinNodePosi(T) & v, const T& e, BinNodePosi(T) & hot ) {
   if ( !v || ( e == v->data ) ) return v; //递归基：在节点v（或假想的通配节点）处命中
   hot = v; //一般情况：先记下当前节点，然后再
   return searchIn ( ( ( e < v->data ) ? v->lc : v->rc ), e, hot ); //深入一层，递归查找
} //返回时，返回值指向命中节点（或假想的通配哨兵），hot指向其父亲（退化时为初始值NULL）

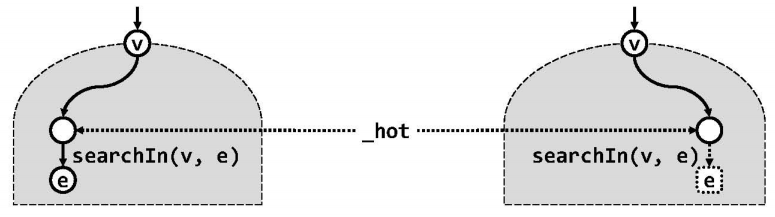
节点插入和删除操作，都需要首先调用查找算法，并根据查找结果确定后续的处理方式。因此这里以引用方式传递（子）树根节点，以为后续操作提供必要的信息。searchIn()采用典型的尾递归来实现。这种实现方式是为了统一并简化后续不同搜索树的各种操作接口的实现，其中的技巧体现于返回值和hot变量的语义约定。

若查找成功，则searchIn()和search()的返回值都指向一个关键码为e且真实存在的节点；若查找失败，则返回值的数值为NULL，但它作为引用将指向最后一次试图转向的空节点。对于后一种情况不妨将此空节点转换为一个数值为e的哨兵节点，这样无论成功与否，查找的返回值总是等效地指向“命中节点”。在整个查找的过程中，hot变量始终指向当前节点的父亲，因此在算法返回时，按照如上定义，_hot将统一指向“命中节点”的父亲。而_hot节点是否拥有另一个孩子与查找成功与否无关。

接着分析查找算法的效率，在二叉搜索树的每一层，查找算法至多访问一个节点，且只需常数时间，故中体所需时间应线性正比与查找路径的长度，或最终返回节点的深度。在最好情况下，目标关键码出现在树根处，只需$O(1)$时间；而规模为n的二叉搜索树，深度在最坏情况下可达$O(n)$，如退化为一条单链，可见最坏情况下查找所需时间为$O(n)$。因此若要控制单词查找在最坏情况下的运行时间，须从控制二叉树的高度入手，后面介绍的平衡二叉树正是基于这一思路而做的改进。

2.2. BST：插入

为了在二叉搜索树中插入一个节点，首先要利用search(e)确定插入位置及方向（左孩子还是右孩子），再将新节点作为叶子插入。若e尚不存在，则_hot为新节点的父亲，v=search(e)为 _hot对新孩子的引用。于是只需令 _hot通过v指向新节点。

如图(a)中的二叉搜索树为例，若欲插入关键码40，则在执行search(40)之后，如图(b)，_hot将指向比较过的最后一个节点46，同时返回其左孩子（此时为空）的位置，于是接下来如图(c)，只需将其作为46的左孩子接入。为了保持二叉搜索树作为数据结构的完整性和一致性，还需从节点 _hot(46)出发，自底而上地逐个更新新插入的节点40的历代祖先的高度。

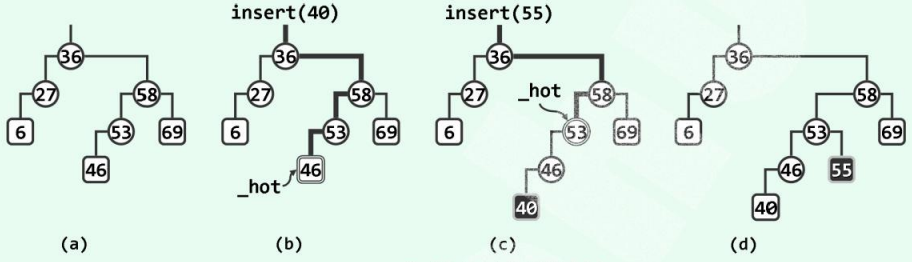
BST的插入算法的代码实现：

template <typename T> BinNodePosi(T) BST<T>::insert ( const T& e ) { //将关键码e插入BST树中
   BinNodePosi(T) & x = search ( e ); if ( x ) return x; //确认目标不存在（留意对_hot的设置）
   x = new BinNode<T> ( e, _hot ); //创建新节点x：以e为关键码，以_hot为父
   _size++; //更新全树规模
   updateHeightAbove ( x ); //更新x及其历代祖先的高度
   return x; //新插入的节点，必为叶子
} //无论e是否存在于原树中，返回时总有x->data == e

按照以上的实现方式，无论插入操作成功与否，都会返回一个非空位置，且该处的节点与拟插入的节点相等，如此可以确保一致性，以简化后续的操作。节点插入操作所需的时间主要消耗于对算法search()和updateHeightAbove()的调用。后者与前者一样都是在每一层至多涉及一个节点，仅消耗$O(1)$时间，故时间复杂度取决于新节点的深度，在最坏情况下不会超过全树的高度$O(h)$。

2.3. BST：删除

为从二叉搜索树中删除节点，首先也要调用search()，判断目标节点是否存在与树中，若存在，则需返回其位置。具体的删除操作要分两种情况来讨论：

单分支情况：

如图(a)欲删除节点69，首先通过search(69)定外待删除节点69，该节点的右子树为空，故只需将69与替换为其左孩子64。为保持二叉搜索树作为数据结构的完整性和一致性，还需要更新全树的规模纪录，释放被摘除的节点69，并自下而上地逐个更新节点64历代祖先的高度。注意，首个需要更新高度的祖先58恰好由_hot指示。以上同时已涵盖左、右孩子均不存在（即目标节点为叶节点）的情况。如此操作之后，二叉搜索树的拓扑结构依然完整，顺序性依然满足。

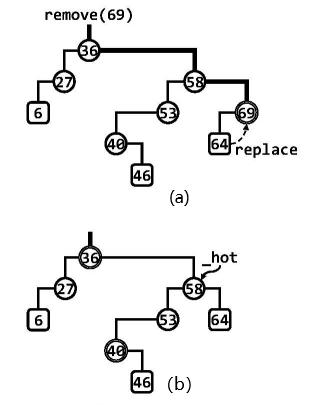
双分支情况：

以上图的二叉树为例，若欲删除节点36，则如图(c)首先调用BinNode::succ()算法找到该节点的直接后继(40)，即中序遍历下的下一个节点，然后交换二者的数据项，则可将后继节点等效地视作待删除的目标节点。而该后继节点必然无左孩子，从而问题转化为上面的单分支情况，于是如图(d)将新的目标节点(36)替换为其右孩子(46)，再释放被摘除的节点(36)，并更新一系列祖先节点的高度，此时首个需要更新高度的祖先，依然恰好由_hot指示，如图(e)。尽管全树的顺序性在中途会不满足，但完成整个删除操作后，全树的顺序性必然恢复。

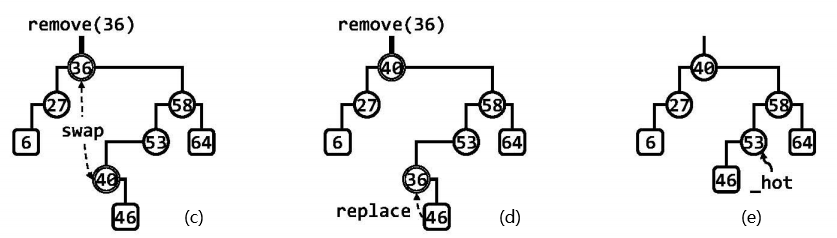
BST的删除算法的代码实现：

template <typename T> bool BST<T>::remove ( const T& e ) { //从BST树中删除关键码e
   BinNodePosi(T) & x = search ( e ); if ( !x ) return false; //确认目标存在（留意_hot的设置）
   removeAt ( x, _hot ); _size--; //实施删除
   updateHeightAbove ( _hot ); //更新_hot及其历代祖先的高度
   return true;
} //删除成功与否，由返回值指示

/**********************************************************************************
 * BST节点删除算法：删除位置x所指的节点（全局静态模板函数，适用于AVL、Splay、RedBlack等各种BST）
 * 目标x在此前经查找定位，并确认非NULL，故必删除成功；与searchIn不同，调用之前不必将hot置空
 * 返回值指向实际被删除节点的接替者，hot指向实际被删除节点的父亲——二者均有可能是NULL
 *********************************************************************************/
template <typename T>
static BinNodePosi(T) removeAt ( BinNodePosi(T) & x, BinNodePosi(T) & hot ) {
   BinNodePosi(T) w = x; //实际被摘除的节点，初值同x
   BinNodePosi(T) succ = NULL; //实际被删除节点的接替者
   if ( !HasLChild ( *x ) ) //若*x的左子树为空，则可
      succ = x = x->rc; //直接将*x替换为其右子树
   else if ( !HasRChild ( *x ) ) //若右子树为空，则可
      succ = x = x->lc; //对称地处理——注意：此时succ != NULL
   else { //若左右子树均存在，则选择x的直接后继作为实际被摘除节点，为此需要
      w = w->succ(); //（在右子树中）找到*x的直接后继*w
      swap ( x->data, w->data ); //交换*x和*w的数据元素
      BinNodePosi(T) u = w->parent;
      ( ( u == x ) ? u->rc : u->lc ) = succ = w->rc; //隔离节点*w
   }
   hot = w->parent; //记录实际被删除节点的父亲
   if ( succ ) succ->parent = hot; //并将被删除节点的接替者与hot相联
   release ( w->data ); release ( w ); return succ; //释放被摘除节点，返回接替者
} //release()负责释放复杂结构，与算法无直接关系

效率：BST的删除操作所需的时间，主要消耗于对search()、succ()和updateHeightAbove()的调用。在树中的任一层，它们各自都至多消耗$O(1)$时间，故总体的渐进时间复杂度，亦不超过全树的高度$O(h)$。

3.平衡二叉搜索树

3.1.树高和性能

由以上的实现与分析，BST主要接口search()，insert()和remove()的运行时间在最坏情况下，均线性正比于其高度$O(h)$，因此若不能有效地控制树高，则就实际的性能而言，较之此前的向量和列表等数据结构，BST将无法体现出明显优势。比如在最坏情况下，二叉搜索树可能彻底地退化为列表，此时的查找效率甚至会降至$O(n)$，线性正比于树（列表）的规模。那么出现此类最坏或较坏情况的概率有多大，或者从平均复杂度的角度看，二叉搜索树的性能究竟如何呢？下面按两种常用的随机统计口径，就BST的平均性能做一分析和对比。

随机生成：

考查n个互异词条$\{e_1,e_2,\dots,e_n\}$，对任一排列$\sigma=(e_{i_1},e_{i_2},\dots,e_{i_n})$，从空树开始，通过依次执行insert($e_{i_k}$)，即可得到这n个关键码的一棵二叉搜索树$T(\sigma)$。与随机排列$\sigma$相对应的$T(\sigma)$称为由$\sigma$随机生成（randomly generated）。下图以关键码为例$\{1,2,3\}$为例，列出了由其所有排列生成的二叉搜索树。

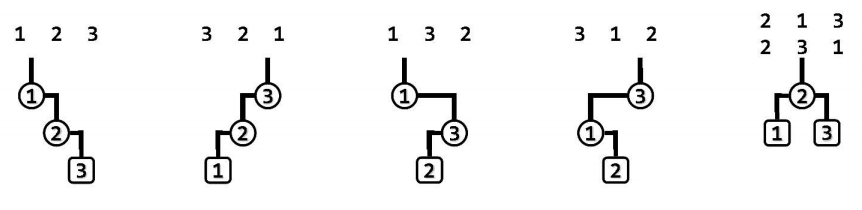
显然任意的n个互异关键码都可以构成$n!$种全排列，若设各排列作为输入序列的概率均等，则在随机生成下二叉搜索树的平均高度为$\Theta(\log n)$。

随机组成：

另一种随机策略是，假定n个互异节点同时给定，然后在遵守顺序性的前提下，随机确定它们之间的拓扑联接关系，如此所得的二叉搜索树，称为由这组节点随机组成（randomly composed）。

由n个互异节点组成的二叉搜索树，总共有：

$$T(n)=\sum_{k=1}^n SP(k-1)\cdot SP(n-k)=Catalan(n)=\frac{(2n)!}{(n+1)!\cdot n!}$$

若设所有BST等概率出现，则其平均高度为$\Theta(\sqrt{n})$。

随机生成口径的$\Theta(\log n)$和随机组成口径的$\Theta(\sqrt{n})$之间就渐进意义为言有实质的差别。原因在于随机生成下，同一组关键码的不同排列所生成的二叉搜索树，未必不同，会发现中位数越早插入，树的高度越低即越平衡，而实际上越是平衡的树，被统计的次数亦越多。从这个角度看，随机生成口径有些“乐观”，高估了二叉搜索树的平均性能，因而按照随机组成口径得到的$\Theta(\sqrt{n})$更可信。

实际上按照随机组成口径统计出的平均树高，仍不足以反映树高的随机分布情况，在实际应用中，理想的随机并不常见，一组关键码往往会按照（接近）单调次序出现，树高较大的情况依然可能频繁出现。另外若removeAt()操作总是固定地将待删除的二度节点与其直接后继交换，则随着操作次数的增加，二叉搜索树向左侧倾斜的趋势将愈发明显。

3.2.理想平衡与适度平衡

理想平衡：

在节点数目固定的前提下，应尽可能地降低高度，相应地应尽可能使兄弟子树的高度彼此接近，即全树尽可能平衡。由n个节点组成的二叉树，高度不低于$\log_2 n$，当高度恰为$\log_2 n$时称作理想平衡，即大致相当于完全二叉树或者满树，但是“叶节点只能出现于最底部的两层”—这一条件过于苛刻。此类二叉树所占的比例极低，而随着二叉树规模的增大，这一比例还将减小，且对二叉树的动态操作很容易就破坏了这种理想操作。

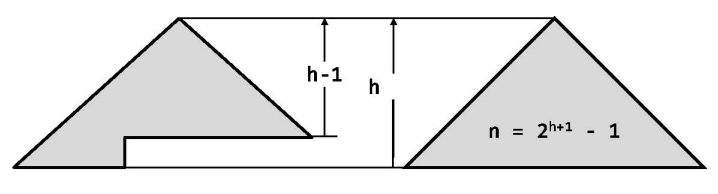
适度平衡：

若将树高限制为“渐进地不超过$O(\log n)$，称作适度平衡。适度平衡的BST称为平衡二叉搜索树（balanced binary search tree，BBST），如之后要介绍的伸展树，红黑树，kd-树等都属于BBST。

3.3.等价变换

3.3.1.等价二叉搜索树

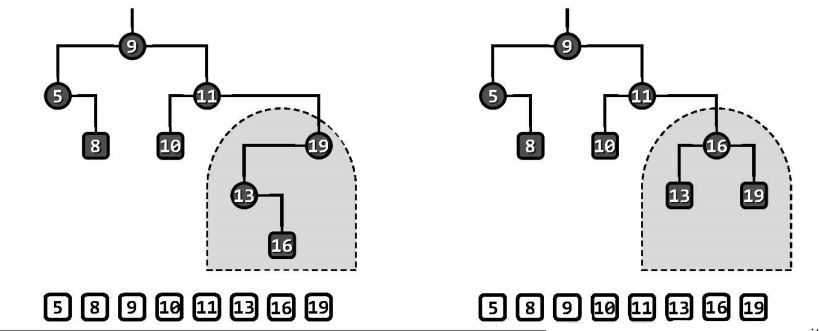
若两棵二叉搜索树的中序遍历序列相同，则称它们彼此等价。如下图两个由11个节点组成的相互等价的二叉搜索树，它们在拓扑关系上有差异。

等价二叉搜索树的特点可概括为：

• 上下可变：联接关系不尽相同，承袭关系可能颠倒
• 左右不乱：中序遍历序列完全一致，全局单调非降

3.3.2.局部性

平衡二叉搜索树的适度平衡性，都是通过对树中每一局部增加某种限制条件来保证的。除了适度平衡性外，还具有如下局部性：

• 单次动态修改操作后，至多$O(1)$处局部不再满足限制条件

• 可在$O( \log n)$时间内，使这些局部（以至全树）重新满足

这就意味着刚刚失去平衡的二叉搜索树，必然可以迅速转换为一棵等价的BBST，等价二叉搜索树之间的上述转换过程，也称作等价变换。

3.3.3.旋转调整

最基本的等价变换方法，即修复局部性失衡的方法，就是通过围绕特定节点的旋转，实现等价前提下的局部拓扑调整。

zig和zag：

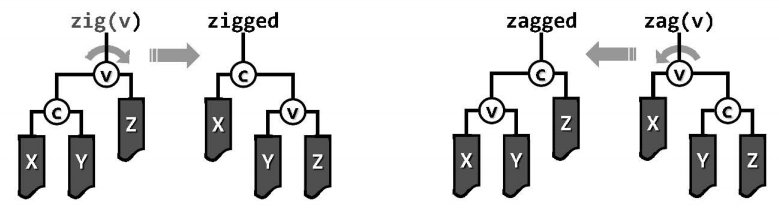
zig和zag旋转均属于局部操作，仅涉及常数个节点及其之间的联接关系，故均可在常数时间内完成。每经过一次zig或zag旋转之后，节点v的深度加一，节点c的深度减一；这一局部子树（乃至全树）的高度可能发生变化，但上下幅度均不超过一层。