0%

数据结构与算法（14）AVL树

发表于 分类于 本文字数： 7.7k
通过合理设定适度平衡的标准，并借助以上等价变换，AVL树可以实现近乎理想的平衡。

AVL树是由G. M. Adelson-Velsky和E. M. Landis与1962年发明的一种平衡二叉搜索树，并以他们名字的首字母命名。通过合理设定适度平衡的标准，并借助以上等价变换，AVL树可以实现近乎理想的平衡。在渐进意义下，AVL树始终将高度控制在$O(\log n)$以内，从而保证每次查找，插入或删除操作，均可在$O(\log n)$的时间内完成。

1.定义及性质

任一节点v的平衡因子（balance factor）定义为“其左、右子树的高度差”，即：

balFac(v) = height( lc(v) ) - height( rc(v) )

在AVL树中，任意节点的平衡因子的绝对值不超过1，即|balFac(v)| $\le$ 1，注意空树高度取-1，单节点子树（叶节点）高度取0。AVL树未必理想平衡，但必然适度平衡。

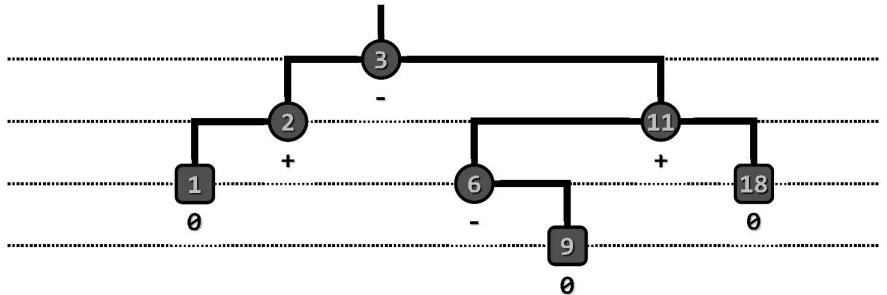
适度平衡要求当节点数固定为n时，树的高度渐进地不超过$O(\log n)$。欲证明AVL树满足适度平衡条件，可转化为证明当树的高度固定时，树中的节点数不会太少。考虑高度为h的所有AVL树，并取S为其中节点数最少的一棵，如下图，$S_L$和$S_R$分别为$S$的左右子树，$S_L$和$S_R$也都是AVL树，而且高度不超过h-1，又因为$S$的节点数最少，所以$S_L$和$S_R$中一个高度为h-1，一个高度为h-2。从而可以得到以下递推关系，并加以整理得到fibonacci数列的形式：

从高度为0，1，2的树的节点数可以推出节点数$S(h)$和fibonacci数的关系，即$S(h)=fib(h+3)$。

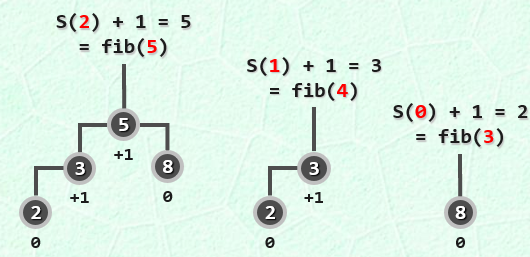
可得对于高度为h的AVL数，节点数n满足$n\ge \Omega(\Phi ^h)$，因此对于节点数固定为n的AVL数，其高度h满足$h\le O(\log n)$。

基于BST模板类，可直接派生出AVL模板类，并根据AVL树的重平衡规则与算法，重写了insert()和remove()接口。另外，为简化对节点平衡性的判断，算法实现时可借用宏定义。

1
2
3
4
5
6
7
8
9
10
#define Balanced(x) ( stature( (x).lc ) == stature( (x).rc ) ) //理想平衡条件
#define BalFac(x) ( stature( (x).lc ) - stature( (x).rc ) ) //平衡因子
#define AvlBalanced(x) ( ( -2 < BalFac(x) ) && ( BalFac(x) < 2 ) ) //AVL平衡条件

template <typename T> class AVL : public BST<T> { //由BST派生AVL树模板类
public:
   BinNodePosi(T) insert ( const T& e ); //插入（重写）
   bool remove ( const T& e ); //删除（重写）
// BST::search()等其余接口可直接沿用
};

按照BST规则插入或删除节点之后，AVL中节点的高度可能会发生变化，平衡性可能会破坏，以致于不再满足AVL树的条件。如此因节点x的插入或删除而暂时失衡的节点，构成失衡的节点集，记作UT(x)。

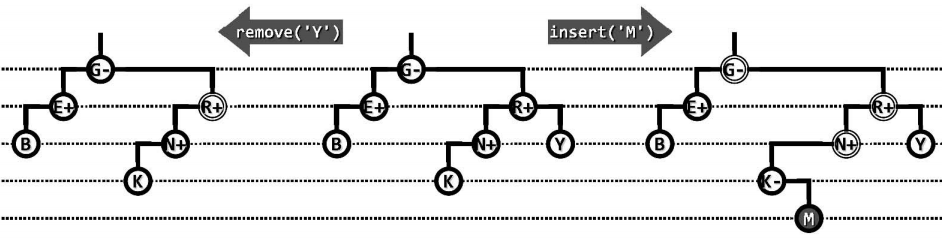
为了恢复AVL的平衡性需要借助等价变换，它有以下优势：

  • 局部性：所有的旋转都在局部进行 //每行只需$O(1)$时间
  • 快速性：在每一深度只需检查并旋转至多一次 //共$O(\log n)$次

2.节点插入

新引入节点x后，UT(x)中的节点都是x的祖先，且高度不低于x的祖父。将其中的最深者记为g(x)，在 x与g(x)的通路上，设p为g(x)的孩子，v为p的孩子，既然g(x)不低于x的祖父，则p必是x的真祖先。

首先需要找到如上定义的g(x)，可以从x出发沿parent指针逐层上行并核对平衡因此，首次遇到的失衡祖先即为g(x)，既然原树是平衡的，故这一过程需要$O(\log n)$。既然g(x)是因x的引入而失衡，则p和v的高度均不低于其各自的兄弟，因此借助宏定义的tallerChild()，即可反过来由g(x)找到p和v。

1
2
3
4
5
6
7
#define tallerChild(x) ( \
   stature( (x)->lc ) > stature( (x)->rc ) ? (x)->lc : ( /*左高*/ \
   stature( (x)->lc ) < stature( (x)->rc ) ? (x)->rc : ( /*右高*/ \
   IsLChild( * (x) ) ? (x)->lc : (x)->rc /*等高：与父亲x同侧者（zIg-zIg或zAg-zAg）优先*/ \
   ) \
   ) \
)

以下根据节点g(x)、p和v之间具体的联接方向，采用不同的局部调整方案。

单旋：

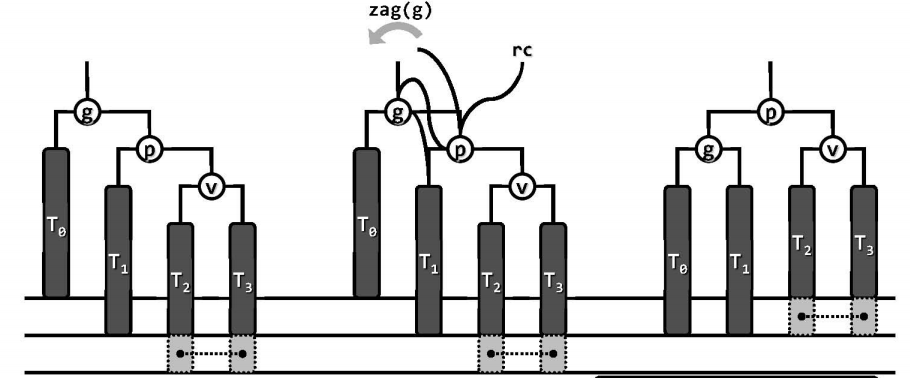
当g、p和v在同一侧时，如下图都在右侧（可称为zag-zag，对称地若都在左侧可称为zig-zig），在$T_2$或者$T_3$处插入新的节点，插入的节点在底部以浅灰色表示，g的平衡因子由原来的-1变为-2，失衡。这种情况只需g经单次旋转zag(g(x))，图中的子树高度复原，更高的祖先也比平衡，全树复衡。

双旋：

当g、p和v不在同一侧时，如下图中p是g的右孩子，v是p的左孩子（可称为zag-zig，对称地若p是g的左孩子，v是p的右孩子可称为zig-zag），在$T_1$或者$T_2$处插入新的节点，插入新节点后，g的平衡因子由原来的-1变为-2，失衡。这种情况需要先做顺时针旋转zig(p)，在做逆时针旋转zag(g)，得到一棵平衡的等价二叉树。

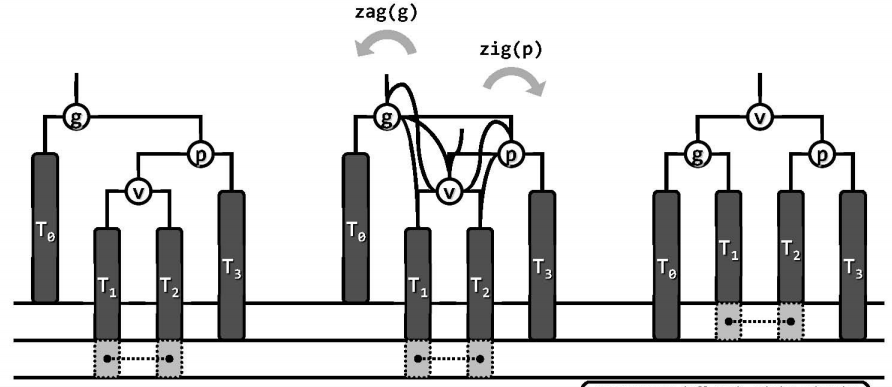
无论单旋还是双旋，经局部调整之后，不仅g(x)能够重获平衡，而且局部子树的高度也必将平衡。这就意味着，g(x)以上所有祖先的平衡因子亦将统一地复原，即在AVL树中插入新节点后，仅需要至多两次旋转，即可使整数恢复平衡。

AVL树插入节点的代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename T> BinNodePosi(T) AVL<T>::insert ( const T& e ) { //将关键码e插入AVL树中
   BinNodePosi(T) & x = search ( e ); if ( x ) return x; //确认目标节点不存在
   BinNodePosi(T) xx = x = new BinNode<T> ( e, _hot ); _size++; //创建新节点x
// 此时，x的父亲_hot若增高，则其祖父有可能失衡
   for ( BinNodePosi(T) g = _hot; g; g = g->parent ) { //从x之父出发向上，逐层检查各代祖先g
      if ( !AvlBalanced ( *g ) ) { //一旦发现g失衡，则（采用“3 + 4”算法）使之复衡，并将子树
         FromParentTo ( *g ) = rotateAt ( tallerChild ( tallerChild ( g ) ) ); //重新接入原树
         break; //g复衡后，局部子树高度必然复原；其祖先亦必如此，故调整随即结束
      } else //否则（g依然平衡），只需简单地
         updateHeight ( g ); //更新其高度（注意：即便g未失衡，高度亦可能增加）
   } //至多只需一次调整；若果真做过调整，则全树高度必然复原
   return xx; //返回新节点位置
} //无论e是否存在于原树中，总有AVL::insert(e)->data == e

效率：该算法首先按照二叉搜索树的常规算法在$O(\log n)$时间内插入新节点x，既然原树是平衡的，故至多坚持$O(\log n)$个节点即可确定g(x)，而至多旋转两次即可使局部乃至全树恢复平衡，因此AVL树的节点插入操作可以在$O(\log n)$时间内完成。

3.节点删除

与插入操作不同的是，在删除节点x后，以及在随后的调整过程中，失衡节点集UT(x)始终至多只含一个节点。若该节点g(x)存在，其高度必与失衡前相同，而且g(x)有可能就是x的父亲。

与插入操作同理，从_hot节点出发沿parent指针上行经过$O(\log n)$时间即可确定g(x)位置，作为失衡节点的g(x)在不包含x的一侧必有一个非空孩子p，且p的高度至少为1。选取p的孩子节点v时可按以下规则：若两个孩子不等高，则v取其中的更高者；若两个孩子等高，则取与p同向者。

以下不妨假设失衡后g(x)的平衡因子为+2，根据g、p和v的关系，通过等价变换，同样可以使得这一局部恢复平衡。

单旋：

如下图g、p和v在同一侧，在$T_3$中删除节点使得节点g(x)失衡，通过一次顺时针旋转zig( g )即可恢复局部的平衡。这里约定图中以虚线连接的灰色方块所对应的节点，不能同时为空；$T_2$底部的灰色方块所对应的节点，可以为空，也可以非空。

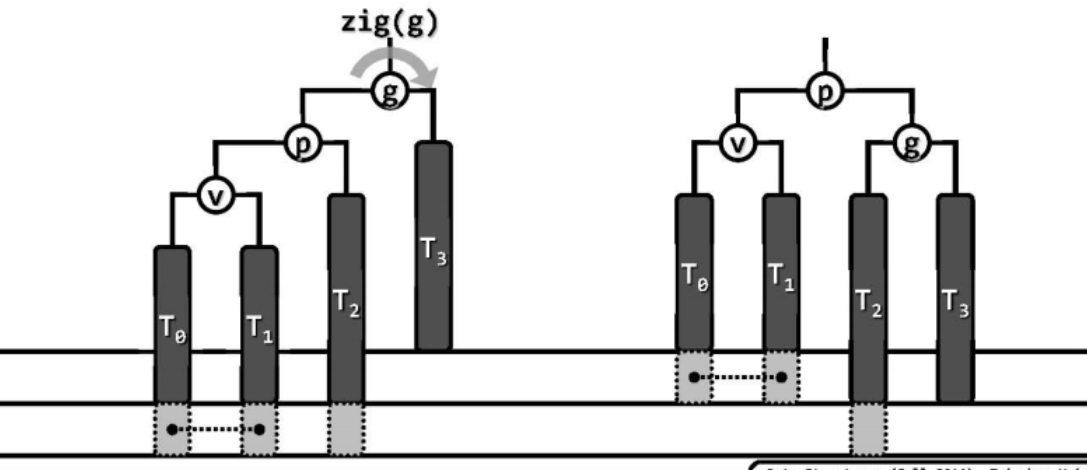
双旋：

如下图g、p和v不在同一侧，在$T_3$中删除节点使得节点g(x)失衡，这种情况需要先做一次逆时针旋转zag( p )，再做一次顺时针旋转zig( g )，即可恢复局部平衡。

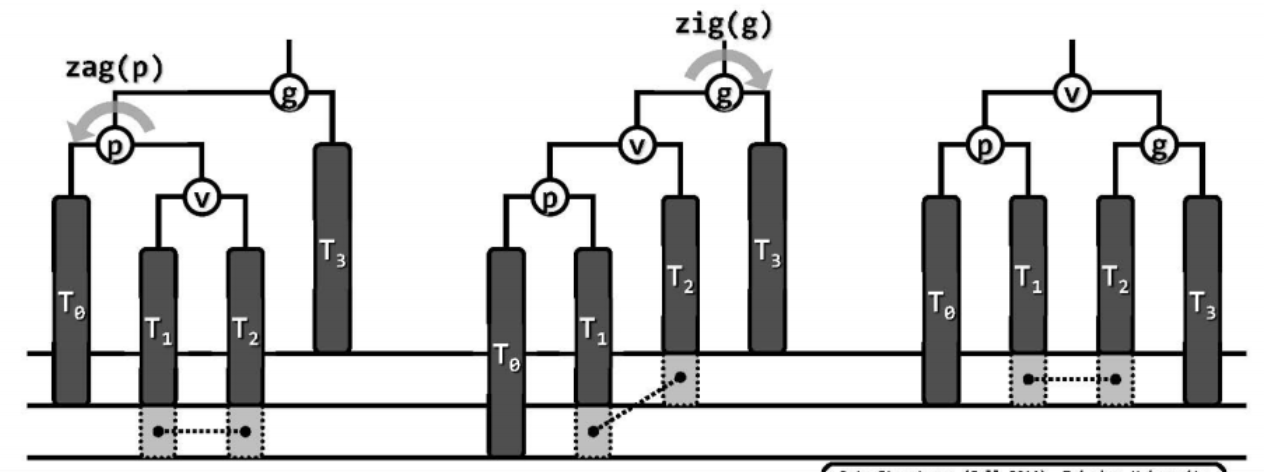
失衡传播：

经过旋转操作使局部恢复平衡后，子树的高度未必复原，如上图中子树的高度降低，因此其更高的祖先可能失衡。在删除节点之后的调整过程中，这种由于低层失衡节点的重平衡而致使其更高层祖先失衡的现象，称作“失衡传播”。

失衡传播的方向必然是自底而上的，因而不致于影响到狗带节点。在此过程中的任一时刻，至多只有一个失衡的节点；高层的某一节点由平衡转为失衡，只能发生在下层失衡节点恢复平衡之后。因此可沿parent指针逐层遍历所有祖先，每找到一个失衡的祖先节点，即可套用以上方法式使之恢复平衡。

AVL树删除节点的代码实现：

1
2
3
4
5
6
7
8
9
10
template <typename T> bool AVL<T>::remove ( const T& e ) { //从AVL树中删除关键码e
   BinNodePosi(T) & x = search ( e ); if ( !x ) return false; //确认目标存在（留意_hot的设置）
   removeAt ( x, _hot ); _size--; //先按BST规则删除之（此后，原节点之父_hot及其祖先均可能失衡）
   for ( BinNodePosi(T) g = _hot; g; g = g->parent ) { //从_hot出发向上，逐层检查各代祖先g
      if ( !AvlBalanced ( *g ) ) //一旦发现g失衡，则（采用“3 + 4”算法）使之复衡，并将该子树联至
         g = FromParentTo ( *g ) = rotateAt ( tallerChild ( tallerChild ( g ) ) ); //原父亲
      updateHeight ( g ); //并更新其高度（注意：即便g未失衡，高度亦可能降低）
   } //可能需做Omega(logn)次调整——无论是否做过调整，全树高度均可能降低
   return true; //删除成功
} //若目标节点存在且被删除，返回true；否则返回false

效率：较之插入操作，删除操作可能需要在重平衡上要多花费 一些时间，既然需要做重平衡的节点都是x的祖先，故重平衡过程累计只需$O(\log n)$时间，因此AVL树的节点删除操作总体的时间复杂度依然是$O(\log n)$。

4.统一重平衡算法

这一节主要解决如何实现第2、3节中插入/删除操作实现代码中的重平衡算法rotateAt()，上述重平衡的方法实质上可以转换成一种更简明的方法，无论是插入或删除操作，都要从刚发生修改的位置x出发向上直到遇到最低的失衡节点g(x)，在g(x)更高一侧的子树中，其孩子节点p和孙子节点v必然存在，按中序遍历次序，将其重命名为：$a < b < c$。它们总共拥有互不相交的四棵（可能为空）子树，按中序遍历序列，将其重命中为：$T_0<T_1<T_2<T_3$。

将原先以g为根的子树S，替换为一棵新子树S’：

等价变换后得到的新子树也是一棵AVL树，保持中序遍历次序：$T_0<a<T_1<b<T_2<c<T_3$。实际上，这一理解涵盖了此前两节所有的单旋和双旋情况（就相当于不进行“旋转”操作，而是直接将节点和子树“拆开”来按中序遍历次序保持不变重新拼到一起，使之恢复平衡）。相应的重构过程，仅涉及局部的三个节点及四棵子树，故称作“ 3 + 4 ”重构。

这种重构算法可以实现为下面的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**********************************************************************************
 * 按照“3 + 4”结构联接3个节点及其四棵子树，返回重组之后的局部子树根节点位置（即b）
 * 子树根节点与上层节点之间的双向联接，均须由上层调用者完成
 * 可用于AVL和RedBlack的局部平衡调整
 *********************************************************************************/
template <typename T> BinNodePosi(T) BST<T>::connect34 (
   BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c,
   BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3
) {
   //*DSA*/print(a); print(b); print(c); printf("\n");
   a->lc = T0; if ( T0 ) T0->parent = a;
   a->rc = T1; if ( T1 ) T1->parent = a; updateHeight ( a );
   c->lc = T2; if ( T2 ) T2->parent = c;
   c->rc = T3; if ( T3 ) T3->parent = c; updateHeight ( c );
   b->lc = a; a->parent = b;
   b->rc = c; c->parent = b; updateHeight ( b );
   return b; //该子树新的根节点
}

根据g、p和v之间的联接关系，可以将g、p和v，以及它们的四棵子树与$a,b,c,T_0,T_1,T_2.T_3$对应起来，如” zig-zig “的联接方式，对应的是connect34(v, p, g, v->lc, v->rc, p->rc, g->rc)；而” zig-zag “的联接方式，对应的是connect34(p, v, g, p->lc, v->lc, v->rc, g->rc)，总之就是按照中序遍历次序代入就可。

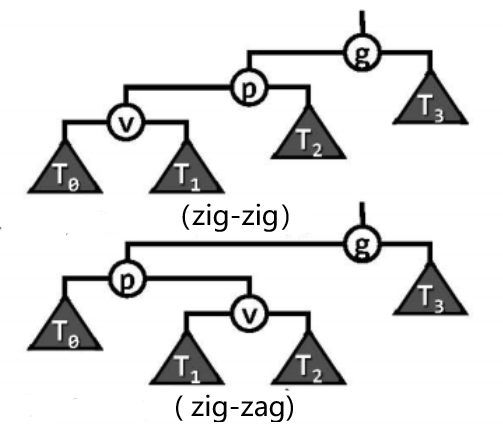
利用connect34()算法，即可视不同情况，按如下的代码实现重平衡算法rotateAt()，rotateAt()算法的复杂度依然是$O(1)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**********************************************************************************
 * BST节点旋转变换统一算法（3节点 + 4子树），返回调整之后局部子树根节点的位置
 * 注意：尽管子树根会正确指向上层节点（如果存在），但反向的联接须由上层函数完成
 *********************************************************************************/
template <typename T> BinNodePosi(T) BST<T>::rotateAt ( BinNodePosi(T) v ) { //v为非空孙辈节点
   /*DSA*/if ( !v ) { printf ( "\a\nFail to rotate a null node\n" ); exit ( -1 ); }
   BinNodePosi(T) p = v->parent; BinNodePosi(T) g = p->parent; //视v、p和g相对位置分四种情况
   if ( IsLChild ( *p ) ) /* zig */
      if ( IsLChild ( *v ) ) { /* zig-zig */ //*DSA*/printf("\tzIg-zIg: ");
         p->parent = g->parent; //向上联接
         return connect34 ( v, p, g, v->lc, v->rc, p->rc, g->rc );
      } else { /* zig-zag */  //*DSA*/printf("\tzIg-zAg: ");
         v->parent = g->parent; //向上联接
         return connect34 ( p, v, g, p->lc, v->lc, v->rc, g->rc );
      }
   else  /* zag */
      if ( IsRChild ( *v ) ) { /* zag-zag */ //*DSA*/printf("\tzAg-zAg: ");
         p->parent = g->parent; //向上联接
         return connect34 ( g, p, v, g->lc, p->lc, v->lc, v->rc );
      } else { /* zag-zig */  //*DSA*/printf("\tzAg-zIg: ");
         v->parent = g->parent; //向上联接
         return connect34 ( g, v, p, g->lc, v->lc, v->rc, p->rc );
      }
}

对AVL树的综合评价：

优点：无论查找、插入或删除，最坏情况下的复杂度均为$O(\log n)$，需要$O(n)$的存储空间。

缺点：需要借助高度或平衡因子，为此需要改造元素结构，或额外封装。实测复杂度与理论值尚有差距，删除操作后，最多需要重平衡$\Omega(\log n)$次，若需频繁地进行插入/删除操作，未免得不偿失。单次动态调整后，全树的拓扑结构的变化量可能高达$\Omega(\log n)$，我们希望将它们控制到更低，比如在下一章将要介绍的红黑树，则可以将这个变化量严格地控制在每次不超过常数无，论对于插入操作还是删除操作都是如此。