0%

数据结构与算法（15）伸展树

发表于 分类于 本文字数： 7.6k
与前一章的AVL树一样，伸展树也是二叉搜索树的一种形式，相对于AVL，伸展树的实现更为简捷。

与前一章的AVL树一样，伸展树也是二叉搜索树的一种形式，相对于AVL，伸展树的实现更为简捷。伸展树无需时刻严格地保持全树的平衡，但却能够在任何足够长的真实操作序列中保持分摊意义上的高效率。伸展树也不需要对基本的二叉树节点结构，做任何附加的要求或改动，更不需要记录平衡平衡因子或高度之类的额外信息，故适用范围更广。

1.构思

1.1.局部性

信息处理的典型模式是，将所有数据项视作一个集合，并将其组织为某种适宜的数据结构，进而借助操作接口高效访问。通常在任意数据结构的生命周期内，不仅执行不同操作的概率往往极不均衡，而且各操作之间具有极强的相关性，并在整体上多呈现出极强的规律性。其中最为典型的，就是所谓的“数据局部性”（data locality），它包括两个方面的含义：

  • 刚刚被访问过的元素，极有可能在不久之后再次被访问到；
  • 将被访问的下一个元素，极有可能就处于不久之前被访问过的某个元素的附近。

充分利用好此类特性，即可进一步地提高数据结构和算法的效率。就二叉搜索树（BST）而言，数据局部性具体表现为：

  • 刚刚被访问过的节点，极有可能在不久之后再次被访问到；
  • 将被访问的下一节点，极有可能就处于不久之前被访问过的某个节点的附近。

因此需要将刚被访问的节点，及时地“转移”至树根（附近），即可加速后续的操作，转移前后的搜索树必须相互等价，为此仍需借助等价变换的技巧。

1.2.逐层伸展

一种直接方式是，每访问过一个节点之后，随即反复地以它的父节点为轴，经适当的旋转将其提升一层，直至最终成为树根。即自下而上，逐层单旋：zig(v->parent)或zag(v->parent)，直至v最终被推送至根。

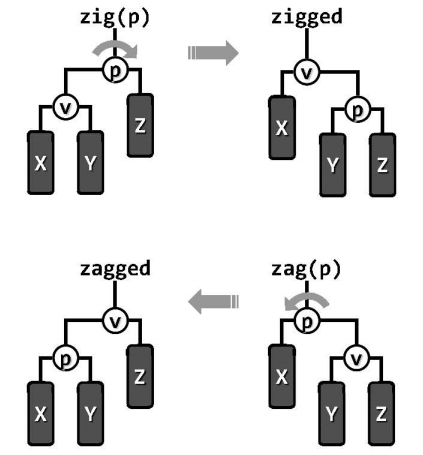
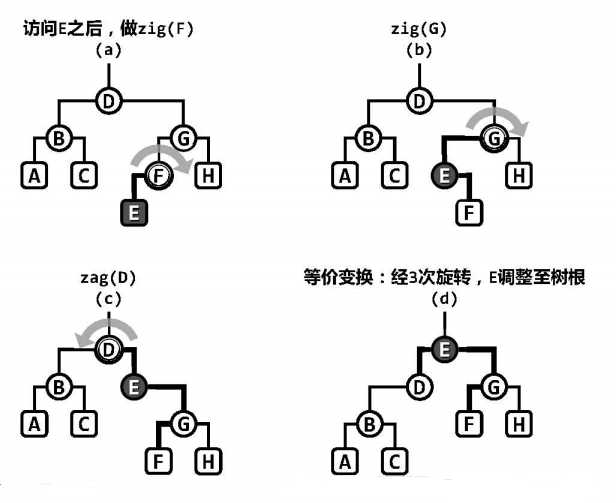
以下图为例，深度为3的节点E刚被访问（查找，插入或“删除”），都可通过3次旋转，将概述等价变换为以E为根的另一颗二叉树。随着节点E的逐层上升，两侧子树的结构也不断地调整，故这一过程也形象地称为伸展（splaying）。

但目前的策略仍存在致命的缺陷——对于很多访问序列，单词访问的分摊时间复杂度在极端情况下可能高达$\Omega(n)$。以下图为例，若从空树开始依次插入关键码$\{1,2,3,4,5\}$，全树的拓扑结构始终呈单链条结构，等价于一维列表。接下来若通过search()接口，再由小到大地依次访问各节点依次，则概述在各次访问之后的结构形态将如图（b~f）所示。

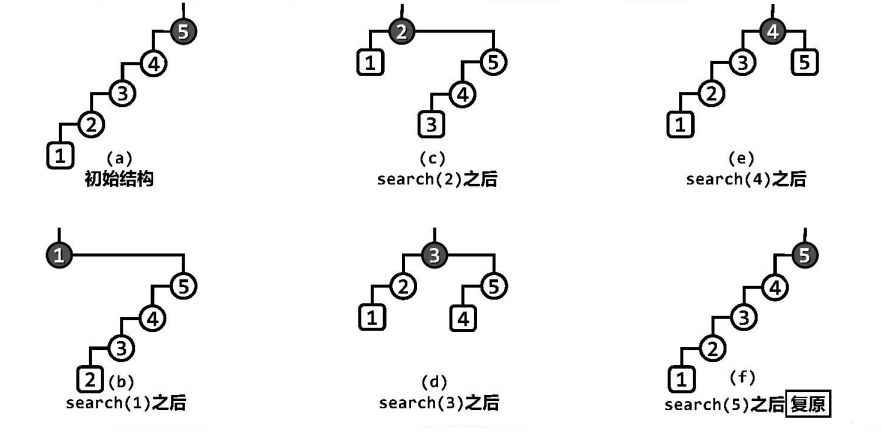
可见在各次访问之后，为将对应节点伸展调整至树根，分别需做$4、4、3、2、1$次旋转。一般地，若节点数为n，则旋转操作的总次数应为：

分摊到每次访问平均需要$\Omega(n)$时间，而这一效率不仅远远低于AVL树，而且甚至与原始的二叉搜索树的最坏情况相当。图(a)与图(f)中二叉树的结构完全相同，也就是说经过以上连续的5次访问之后，全树的结构将会复原，这就意味着以上情况可以持续地再现。

这一访问序列导致$\Omega(n)$平均单次访问时间的原因，可以解释为：在这一可持续重复的过程中，二叉搜索树的高度始终不小于$\lfloor n/2 \rfloor$（向下取整）；而且至少有一半的节点在接受访问时，不仅没有靠近树根，而且反过来恰好处于最底层。从树高的角度看，问题根源也可再进一步地解释为：在持续访问的过程中，树高依算术级数逐步从$n-1$递减到$\lfloor n/2 \rfloor$，然后在逐步递增回到$n-1$。

1.3.双层伸展

为克服上述伸展调整策略的缺陷，一种简便且有效的方法就是：将逐层伸展改为双层伸展。具体地，每次都从当前节点v向上追溯两层（而不是仅一层），并根据其父亲p以及祖父g的相对位置，进行相应的旋转，可分为三种具体的情况：

zig - zag / zag - zig：（与AVL树的双旋等效，与逐层伸展也别无二致）

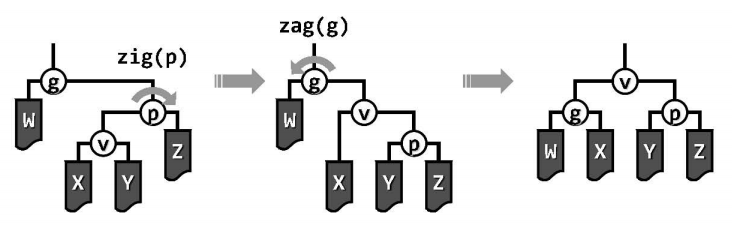
zig - zig / zag - zag：

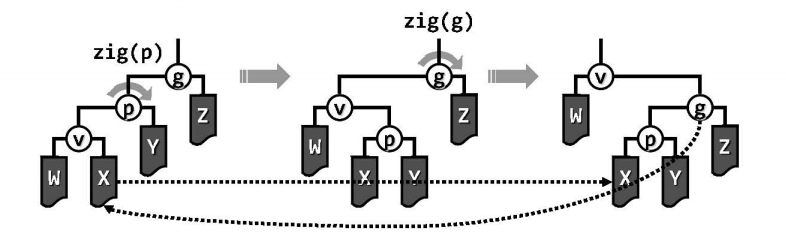
注意顺序是先p后g，若颠倒次序，局部的细微差别将彻底地改变整体（p变成了g的父亲）

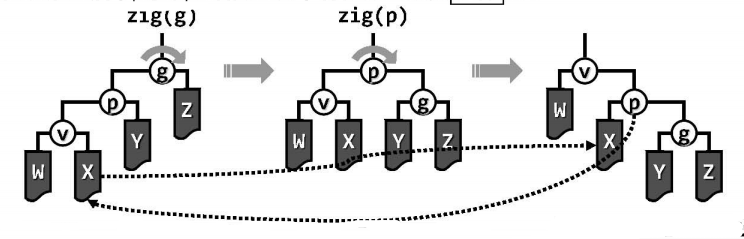
zig / zag：

若v最初的深度为奇数，则经过若干次双层调整至最后一次调整时，v的父亲p即是树根r。此时必有parent(v) == root(T)，且每轮调整中这种情况至多（在最后）出现一次。

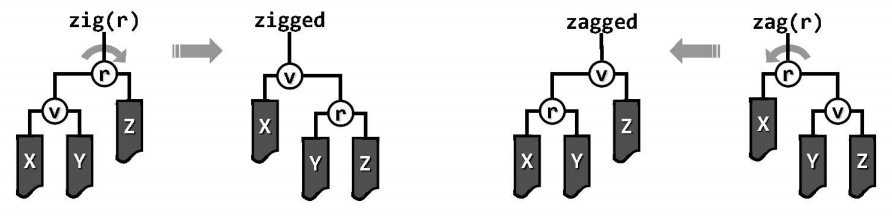
与逐层伸展相比，双层伸展中的zig-zag和zag-zig调整与逐层伸展完全一致，而zig-zig和zag-zag调整则有所不同，事实上后者才是双层伸展策略优于逐层伸展策略的关键所在。

以下图为例做一个对比，最深节点(1)被访问之后再经过双层调整，不仅同样可将该节点伸展至树根，而且同时可使树的高度接近于减半。

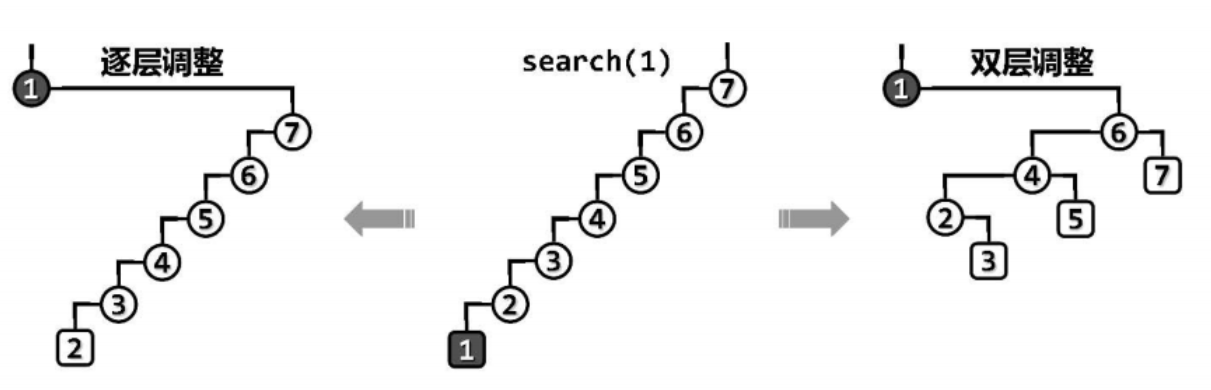
即树的形态而言，双层伸展策略可“智能”地折叠被访问的子树分支，从而有效地避免对长分支的连续访问，这就意味着即使节点v的深度为$\Omega(n)$，双层伸展策略即可将v推至树根，亦可令对应分支的长度以几何级数（大致折半）的速度收缩。

通过双层伸展的策略，伸展树虽不能杜绝最坏情况的发生，却能有效地控制最坏情况发生的频度，从而在分摊意义上保证整体的高效率。Tarjan等人证明了伸展树的单次操作均可在分摊的$O(\log n)$时间内完成。

2.实现

2.1.接口定义

基于BST类，可定义伸展树模板类Splay，直接沿用二叉搜索树类，并根据伸展树的平衡规则，重写了上基本操作接口search()，insert()和remove()，另外针对伸展树调整操作，设有一个内部保护型接口splay()。

1
2
3
4
5
6
7
8
9
#include "BST/BST.h" //基于BST实现Splay
template <typename T> class Splay : public BST<T> { //由BST派生的Splay树模板类
protected:
   BinNodePosi(T) splay ( BinNodePosi(T) v ); //将节点v伸展至根
public:
   BinNodePosi(T) & search ( const T& e ); //查找（重写）
   BinNodePosi(T) insert ( const T& e ); //插入（重写）
   bool remove ( const T& e ); //删除（重写）
};

2.2.调整算法

双层伸展的调整方法，可实现为一下的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
template <typename NodePosi> inline //在节点*p与*lc（可能为空）之间建立父（左）子关系
void attachAsLChild ( NodePosi p, NodePosi lc ) { p->lc = lc; if ( lc ) lc->parent = p; }

template <typename NodePosi> inline //在节点*p与*rc（可能为空）之间建立父（右）子关系
void attachAsRChild ( NodePosi p, NodePosi rc ) { p->rc = rc; if ( rc ) rc->parent = p; }

template <typename T> //Splay树伸展算法：从节点v出发逐层伸展
BinNodePosi(T) Splay<T>::splay ( BinNodePosi(T) v ) { //v为因最近访问而需伸展的节点位置
   if ( !v ) return NULL; BinNodePosi(T) p; BinNodePosi(T) g; //*v的父亲与祖父
   while ( ( p = v->parent ) && ( g = p->parent ) ) { //自下而上，反复对*v做双层伸展
      BinNodePosi(T) gg = g->parent; //每轮之后*v都以原曾祖父（great-grand parent）为父
      if ( IsLChild ( *v ) )
         if ( IsLChild ( *p ) ) { //zig-zig
            /*DSA*/printf ( "\tzIg-zIg :" ); print ( g ); print ( p ); print ( v ); printf ( "\n" );
            attachAsLChild ( g, p->rc ); attachAsLChild ( p, v->rc );
            attachAsRChild ( p, g ); attachAsRChild ( v, p );
         } else { //zig-zag
            /*DSA*/printf ( "\tzIg-zAg :" ); print ( g ); print ( p ); print ( v ); printf ( "\n" );
            attachAsLChild ( p, v->rc ); attachAsRChild ( g, v->lc );
            attachAsLChild ( v, g ); attachAsRChild ( v, p );
         }
      else if ( IsRChild ( *p ) ) { //zag-zag
         /*DSA*/printf ( "\tzAg-zAg :" ); print ( g ); print ( p ); print ( v ); printf ( "\n" );
         attachAsRChild ( g, p->lc ); attachAsRChild ( p, v->lc );
         attachAsLChild ( p, g ); attachAsLChild ( v, p );
      } else { //zag-zig
         /*DSA*/printf ( "\tzAg-zIg :" ); print ( g ); print ( p ); print ( v ); printf ( "\n" );
         attachAsRChild ( p, v->lc ); attachAsLChild ( g, v->rc );
         attachAsRChild ( v, g ); attachAsLChild ( v, p );
      }
      if ( !gg ) v->parent = NULL; //若*v原先的曾祖父*gg不存在，则*v现在应为树根
      else //否则，*gg此后应该以*v作为左或右孩子
         ( g == gg->lc ) ? attachAsLChild ( gg, v ) : attachAsRChild ( gg, v );
      updateHeight ( g ); updateHeight ( p ); updateHeight ( v );
   } //双层伸展结束时，必有g == NULL，但p可能非空
   if ( p = v->parent ) { //若p果真非空，则额外再做一次单旋
      /*DSA*/if ( IsLChild ( *v ) ) { printf ( "\tzIg :" ); print ( p ); print ( v ); printf ( "\n" ); }
      /*DSA*/else              { printf ( "\tzAg :" ); print ( p ); print ( v ); printf ( "\n" ); }
      if ( IsLChild ( *v ) ) { attachAsLChild ( p, v->rc ); attachAsRChild ( v, p ); }
      else                   { attachAsRChild ( p, v->lc ); attachAsLChild ( v, p ); }
      updateHeight ( p ); updateHeight ( v );
   }
   v->parent = NULL; return v;
} //调整之后新树根应为被伸展的节点，故返回该节点的位置以便上层函数更新树根

2.3.查找

在伸展树中查找任一关键e，首先调用二叉搜索树BST的通用算法searchIn()，尝试查找具有关键码e的节点，无论查找是否成功，都继而调用splay()算法，将查找终止位置处的节点伸展到树根。

1
2
3
4
5
template <typename T> BinNodePosi(T) & Splay<T>::search ( const T& e ) { //在伸展树中查找e
   BinNodePosi(T) p = searchIn ( _root, e, _hot = NULL );
   _root = splay ( p ? p : _hot ); //将最后一个被访问的节点伸展至根
   return _root;
} //与其它BST不同，无论查找成功与否，_root都指向最后被访问的节点

2.4.插入

为将关键码e插至伸展树T中，首先调用伸展树查找接口Splay::search(e)查找该关键码。于是最后被访问的节点t，将通过伸展树被提升为树根，其左右子树分别被记为$T_L$和$T_R$。接下来，根据e与t的大小关系，以t为界将T分裂为两棵子树。如设e大于t，可切断t与其右孩子之间的联系，再将以e为关键码的新节点v作为树根，并以t作为其左孩子，以$T_R$作为其右子树。v小于t的情况与此完全对称。

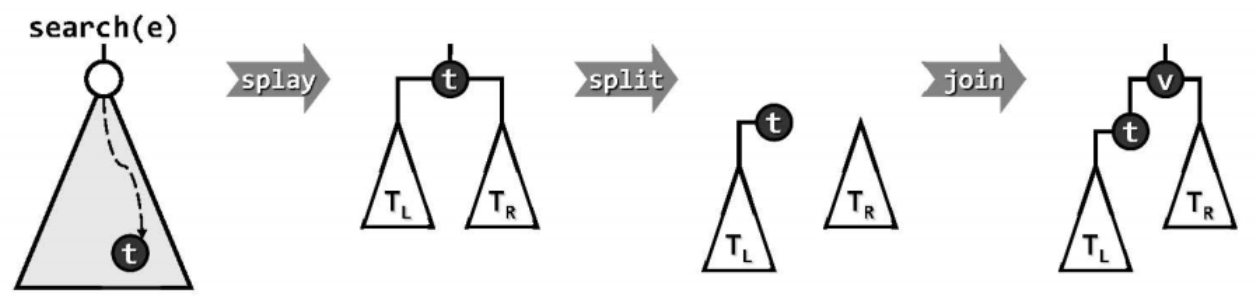
伸展树的插入算法的具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template <typename T> BinNodePosi(T) Splay<T>::insert ( const T& e ) { //将关键码e插入伸展树中
   if ( !_root ) { _size++; return _root = new BinNode<T> ( e ); } //处理原树为空的退化情况
   if ( e == search ( e )->data ) return _root; //确认目标节点不存在
   _size++; BinNodePosi(T) t = _root; //创建新节点。以下调整<=7个指针以完成局部重构
   if ( _root->data < e ) { //插入新根，以t和t->rc为左、右孩子
      t->parent = _root = new BinNode<T> ( e, NULL, t, t->rc ); //2 + 3个
      if ( HasRChild ( *t ) ) { t->rc->parent = _root; t->rc = NULL; } //<= 2个
   } else { //插入新根，以t->lc和t为左、右孩子
      t->parent = _root = new BinNode<T> ( e, NULL, t->lc, t ); //2 + 3个
      if ( HasLChild ( *t ) ) { t->lc->parent = _root; t->lc = NULL; } //<= 2个
   }
   updateHeightAbove ( t ); //更新t及其祖先（实际上只有_root一个）的高度
   return _root; //新节点必然置于树根，返回之
} //无论e是否存在于原树中，返回时总有_root->data == e

尽管伸展树并不需要记录和维护节点的高度，为与其他平衡二叉搜索树的实现保持统一，这里对节点的高度做了及时的更新，在实际应用中可视情况省略这类更新。

2.5.删除

为从伸展树T中删除关键码为e的节点，首先亦调用接口Splay::search(e)查找该关键码，且不妨设命中节点为v。于是v将随机通过伸展被提升为树根，其左右子树分别记作$T_L$和$T_R$。接下来将v摘除，然后在$T_R$中再次查找关键码e，尽管这一查找注定失败，却可以将$T_R$中的最小节点m伸展提升为树根。

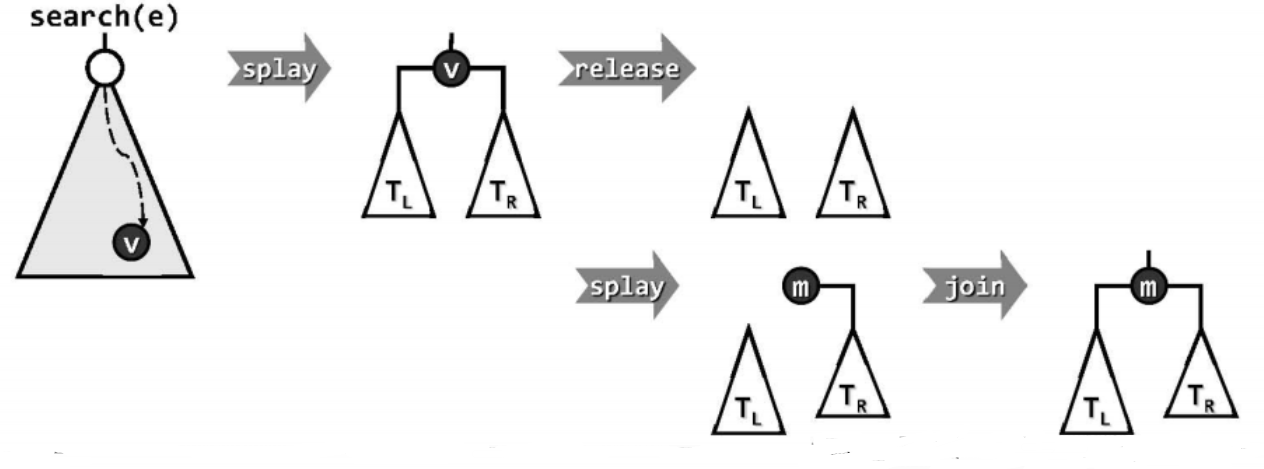
得益于二叉搜索树的顺序性，此时节点m的左子树必然为空；同时$T_L$中所有节点都小于m，于是只需将$T_L$作为左子树与m相互连接，即可得到一棵完整的二叉搜索树。这样不仅删除了v，而且既然新树根m在原树中是v的直接后继，故数据局部性也得到了利用。当然其中第二次查找也可在$T_L$（若非空）中进行。

伸展的删除算法的具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template <typename T> bool Splay<T>::remove ( const T& e ) { //从伸展树中删除关键码e
   if ( !_root || ( e != search ( e )->data ) ) return false; //若树空或目标不存在，则无法删除
   BinNodePosi(T) w = _root; //assert: 经search()后节点e已被伸展至树根
   if ( !HasLChild ( *_root ) ) { //若无左子树，则直接删除
      _root = _root->rc; if ( _root ) _root->parent = NULL;
   } else if ( !HasRChild ( *_root ) ) { //若无右子树，也直接删除
      _root = _root->lc; if ( _root ) _root->parent = NULL;
   } else { //若左右子树同时存在，则
      BinNodePosi(T) lTree = _root->lc;
      lTree->parent = NULL; _root->lc = NULL; //暂时将左子树切除
      _root = _root->rc; _root->parent = NULL; //只保留右子树
      search ( w->data ); //以原树根为目标，做一次（必定失败的）查找
///// assert: 至此，右子树中最小节点必伸展至根，且（因无雷同节点）其左子树必空，于是
      _root->lc = lTree; lTree->parent = _root; //只需将原左子树接回原位即可
   }
   release ( w->data ); release ( w ); _size--; //释放节点，更新规模
   if ( _root ) updateHeight ( _root ); //此后，若树非空，则树根的高度需要更新
   return true; //返回成功标志
} //若目标节点存在且被删除，返回true；否则返回false

2.6.优缺点

优点：

  • 无需记录节点高度或平衡因子；编程实现简单易行 //优于AVL树

    分摊复杂度$O(\log n)$——与AVL树相当

  • 局部性强、缓存命中率极高时（即k << n << m）

    效率甚至可以更高——自适应的$O(\ log k)$，任何连续的m次查找，都可在$O(m\log k + n \log n)$时间内完成。

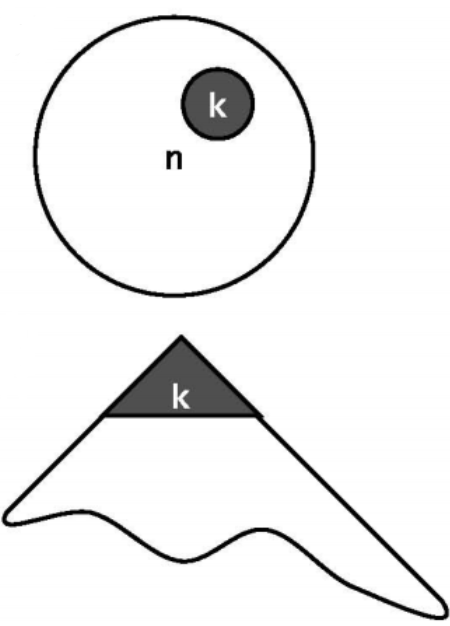
缺点：

  • 仍不能保证单词最坏情况的出现 //不适用于对效率敏感的场合
  • 复杂度的分析稍显复杂