数据结构与算法（16）B-树

1.构思

1.1.分级存储

从实际应用的需求来看，问题规模的膨胀远远快于存储能力的增长。在同等成本下，存储器的容量越大则访问速度越慢，因此一味地提高存储器容量，亦非解决这一矛盾的良策。实践证明，分级存储才是行之有效的方法。在由内存与外存（磁盘）组成的二阶存储系统中，数据全集往往存放于外存中，计算过程中则可将内存作为外存的高速缓存，存放最常用数据项的复本。借助高效的调度算法，如此便可将内存的“高速度”与外存的“大容量”结合起来。

两个相邻存储级别之间的数据传输，统称I/O操作。各级存储器的访问速度相差悬殊，故应尽可能地减少I/O操作。仍以内存与磁盘为例，其单次访问延迟大致分别在纳秒（ns）和毫秒（ms）级别，相差5至6个数量级。因此在衡量相关算法的性能时，基本可以忽略对内存的访问，转而更多地关注对外存的访问次数。

1.2.多路搜索树

当数据规模大道内存已不足以容纳时，常规平衡二叉搜索树的效率将大打折扣，其原因在于，查找过程对外存的访问次数过多。为此，需要充分利用磁盘之类外部存储器的另一特性：就时间成本而言，读取物理地址连续的一千个字节，与读取单个字节几乎没有区别。因此不妨通过时间成本相对较低的多次内存操作，来代替时间成本相对极高的单次外存操作。相应地需要将通常的二叉搜索树，改造为多路搜索树——在中序遍历的意义下，这也是一种等价变换。

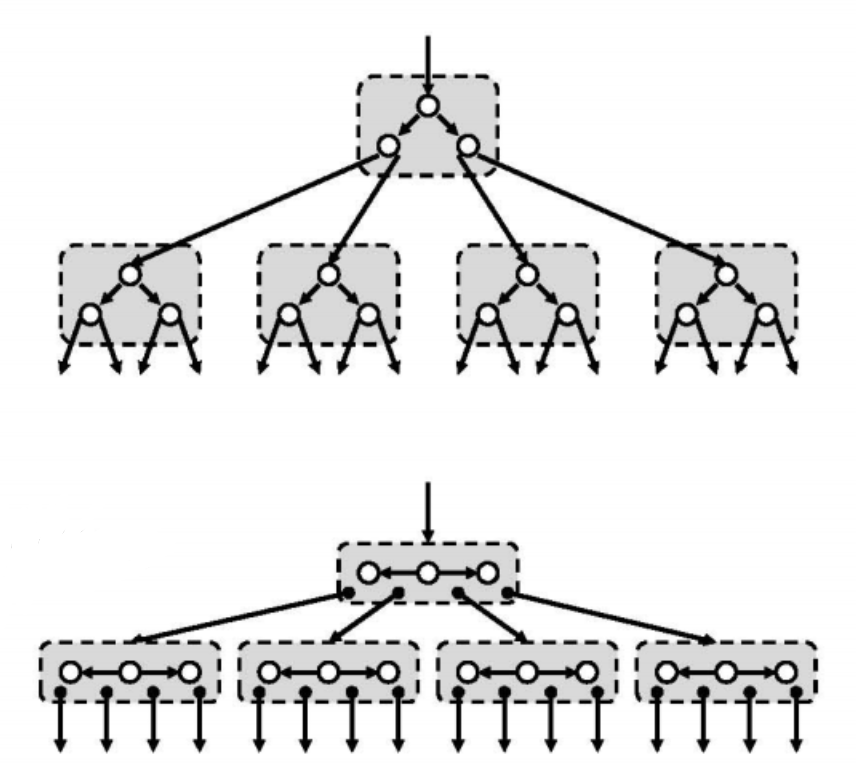
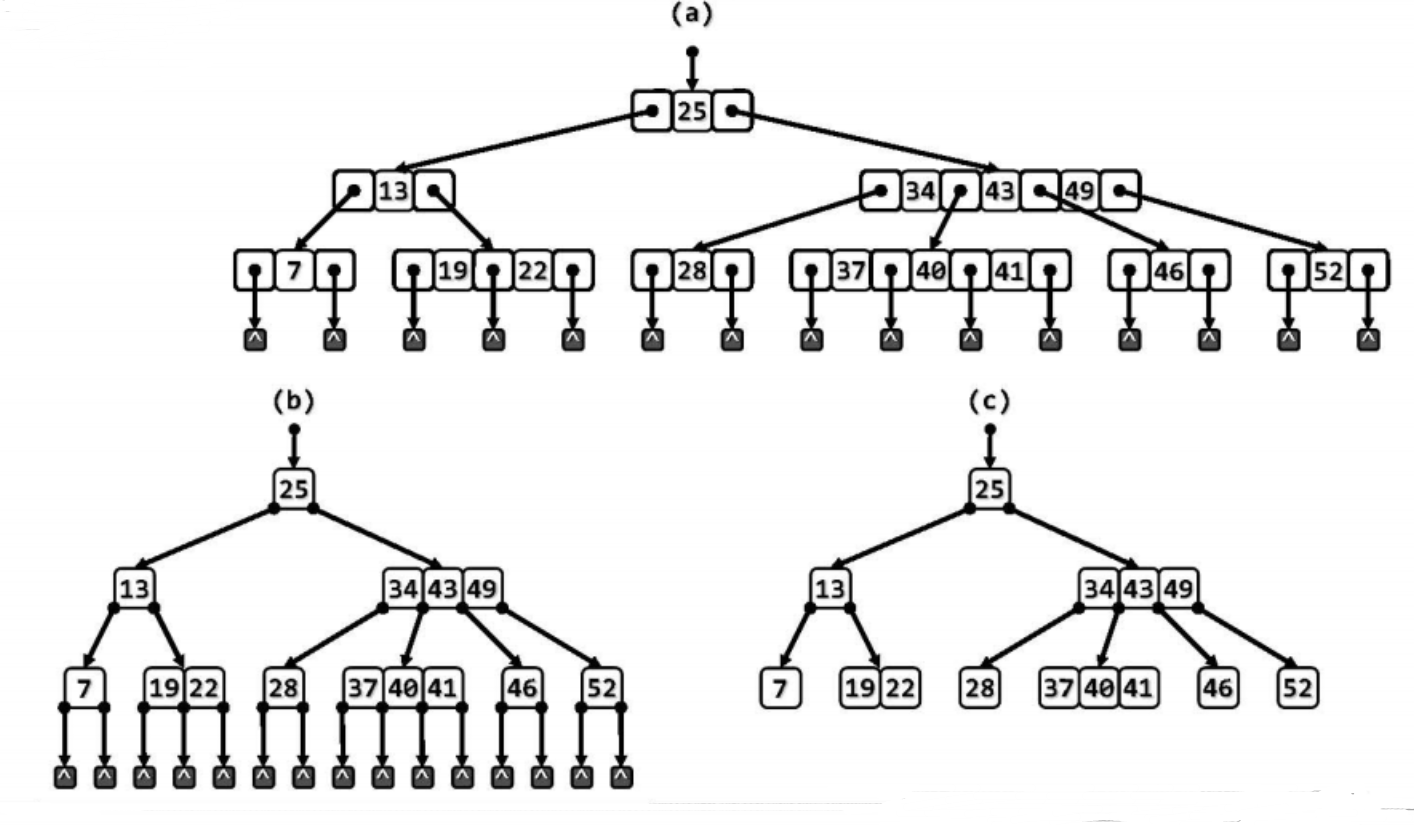
如上图，以两层为间隔，将各节点与其左右孩子合并为“大节点”，每个大节点有四个分支，故称作四路搜索树。一般地，以k层为间隔如此重组，可将二叉搜索树转化为等价的2^k路搜索树，统称为多路搜索树（multi - way search tree）。

多路搜索树在逻辑上与BBST等价，同样支持查找等操作，且效果与原二叉搜索树完全等同；然而重要的是，其对外存的访问方式已发生本质变化。实际上，在此时的搜索等下降一层，都以“大节点”为单位从外存读取一组（而不再是单个）关键码，这组关键码在逻辑上与物理上都彼此相邻，故可以批量方式从外存一次性读出，且所需时间与读取单个关键码几乎一样。而每组关键码的最佳数目，取决于不同外存的批量访问特性。

1.3.多路平衡搜索树

所谓m阶B-树（B-tree），即m路平衡搜索树（m$\ge$2）。其中所有外部节点均深度相等。同时，每个内部节点都存有不超过m-1个关键码，以及用以指示对应分支的不超过m个引用。

具体地，存有$n\le m-1$个关键码：$K_1<K_2<K_3<K_4<\dots<K_n$的内部节点，同时还配有$n+1<m$个引用：$A_0<A_1<A_2<A_3<A_4<\dots<A_n$。

反过来，各内部节点的分支数也不能太少，除根以外的所有内部节点，都应满足：$n+1\ge \lceil m/2 \rceil$，而在非空的B-树中，根节点应满足：$n+1\ge2$。

由于个节点的分支数介于$\lceil m/2 \rceil$至$m$之间，故m阶B-树也称作$(\lceil m/2 \rceil),m)$-树，如(2,3)-树、(3,6)-树或(7,13)-树等。

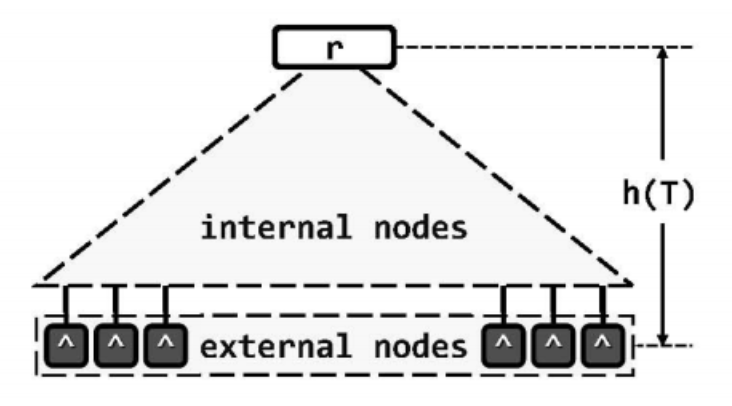
B-树的外部节点（external node）实际上未必意味着查找失败，而可能表示目标关键码存在与更低层的某一次外部存储系统中，顺着该节点的指示，即可深入至下一级存储系统并继续查找。正因如此，在计算B-树高度时，还需要计入其最底层的外部节点。

作为与二叉搜索树等价的“扁平化”版本，B-树的宽度（亦即最底层外部节点的数目）往往远大于其高度。既然外部节点均同处于最底层，且深度完全一致，故用图表示时在将它们省略，可由下图(a)进一步精简为下图(c)的紧凑形式：

2.实现

2.1.ADT接口

按照以上定义，可以模板类的形式描述并实现B-树节点以及B-树结构。B-树节点BTNode类，可实现如以下的代码，这里，同一个节点的所有孩子组织为一个向量，各相邻孩子之间的关键码也组织为一个向量。当然按照B-树的定义，孩子向量的实际长度总是比关键码向量多一。

#include "vector/vector.h"
#define BTNodePosi(T) BTNode<T>* //B-树节点位置

template <typename T> struct BTNode { //B-树节点模板类
// 成员（为简化描述起见统一开放，读者可根据需要进一步封装）
   BTNodePosi(T) parent; //父节点
   Vector<T> key; //关键码向量
   Vector<BTNodePosi(T)> child; //孩子向量（其长度总比key多一）
// 构造函数（注意：BTNode只能作为根节点创建，而且初始时有0个关键码和1个空孩子指针）
   BTNode() { parent = NULL; child.insert ( 0, NULL ); }
   BTNode ( T e, BTNodePosi(T) lc = NULL, BTNodePosi(T) rc = NULL ) {
      parent = NULL; //作为根节点，而且初始时
      key.insert ( 0, e ); //只有一个关键码，以及
      child.insert ( 0, lc ); child.insert ( 1, rc ); //两个孩子
      if ( lc ) lc->parent = this; if ( rc ) rc->parent = this;
   }
};

B-树模板类可实现为如下代码：

#include "BTNode.h" //引入B-树节点类

template <typename T> class BTree { //B-树模板类
protected:
   int _size; //存放的关键码总数
   int _order; //B-树的阶次，至少为3——创建时指定，一般不能修改
   BTNodePosi(T) _root; //根节点
   BTNodePosi(T) _hot; //BTree::search()最后访问的非空（除非树空）的节点位置
   void solveOverflow ( BTNodePosi(T) ); //因插入而上溢之后的分裂处理
   void solveUnderflow ( BTNodePosi(T) ); //因删除而下溢之后的合并处理
public:
   BTree ( int order = 3 ) : _order ( order ), _size ( 0 ) //构造函数：默认为最低的3阶
   { _root = new BTNode<T>(); }
   ~BTree() { if ( _root ) release ( _root ); } //析构函数：释放所有节点
   int const order() { return _order; } //阶次
   int const size() { return _size; } //规模
   BTNodePosi(T) & root() { return _root; } //树根
   bool empty() const { return !_root; } //判空
   BTNodePosi(T) search ( const T& e ); //查找
   bool insert ( const T& e ); //插入
   bool remove ( const T& e ); //删除
}; //BTree

后面会看到，B-树的关键码插入操作和删除操作，可能会引发节点的上溢和下溢，因此这里设有内部接口solveOverflow()和solveUnderflow()，分别用于修正此类问题。

2.2.关键码查找

B-树结构非常适宜于在相对更小的内存中，实现对大规模数据的高效操作。可以将大数据集组织为B-树并存放与外存，对于活跃的B-树，其根节点会常驻于内存，此外任何时刻通常只有另一节点（称作当前节点）留住于内存。

B-树的查找过程，与二次搜索树的查找过程基本类似：首先以根节点作为当前节点，然后再逐层深入。若在当前节点（所包含的一组关键码）中能够找到目标关键码，则成功返回。否则必在当前节点中确定某一个引用（“失败”位置），并通过它转至逻辑上处于下一层的另一节点。若该节点不是外部节点，则将其载入内存，并更新为当前节点，然后继续重复上述过程。

整个过程如下图所示，从根节点开始，通过关键码的比较不断深入至下一层，直到某一关键码命中（查找成功），或者到达某一外部节点（查找失败）。

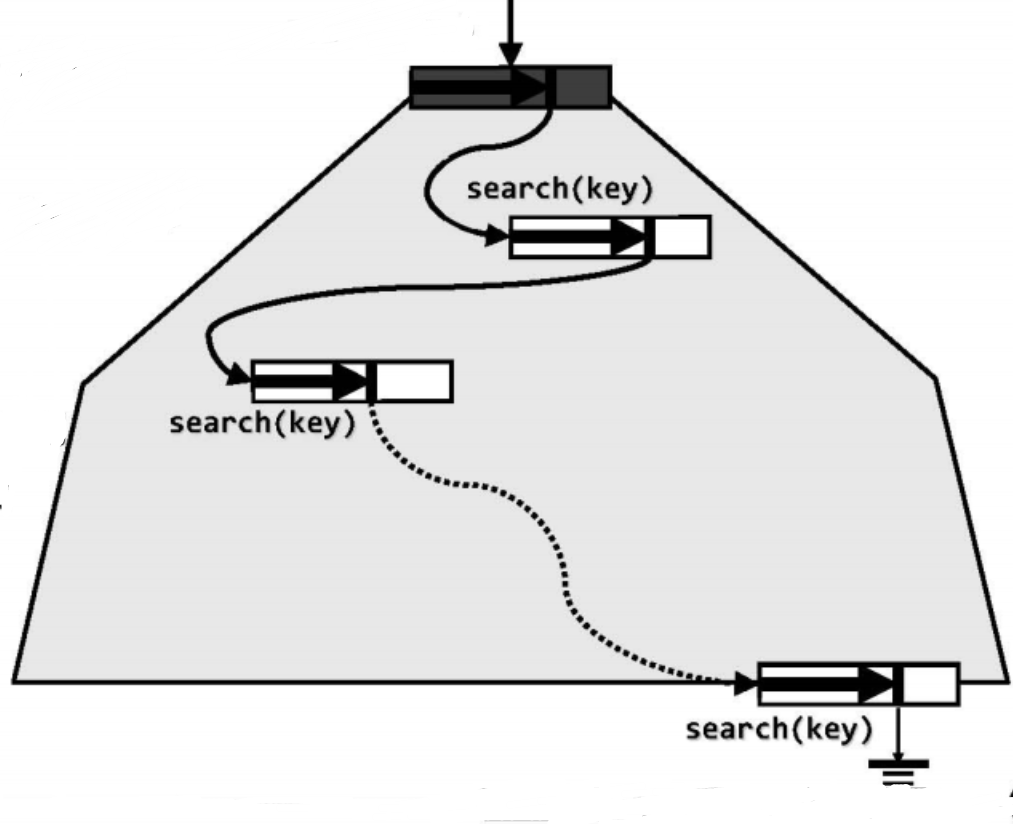
与BST的不同之处在于，因此时各节点内通常都包含多个关键码，故有可能需要经过（在内存中的）多次比较，才能确定应该转向下一层的哪个节点并继续查找。

只有在切换和更新当前节点时才会发生I/O操作，而在同一节点内部的查找则完全在内存中进行。因内存的访问速度远远高于外存，再考虑到各节点所含关键码数量通常在128~512之间，故可直接使用顺序查找策略，而不必采用二分查找之类的复杂策略。

B-树的关键码查找算法实现如下：

template <typename T> BTNodePosi(T) BTree<T>::search ( const T& e ) { //在B-树中查找关键码e
   BTNodePosi(T) v = _root; _hot = NULL; //从根节点出发
   while ( v ) { //逐层查找
      Rank r = v->key.search ( e ); //在当前节点中，找到不大于e的最大关键码
      if ( ( 0 <= r ) && ( e == v->key[r] ) ) return v; //成功：在当前节点中命中目标关键码
      _hot = v; v = v->child[r + 1]; //否则，转入对应子树（_hot指向其父）——需做I/O，最费时间
   } //这里在向量内是二分查找，但对通常的_order可直接顺序查找
   return NULL; //失败：最终抵达外部节点
}

与BST的查找实现类似，这里也约定查找结果由返回的节点位置指代：成功时返回目标关键码所在的节点，上层调用过程可在该节点内进一步查找以确定准确的命中位置；失败时返回对外部节点，其父亲节点则由变量_hot指代。

性能分析：

由上可见，B-树查找操作所需的时间不外乎消耗于两个方面：将某一节点载入内存，以及在内存中对当前节点进行查找。鉴于内存、外存在访问速度上的句法差异，相对于前一类时间消耗，后一类时间消耗可以忽略不计，即B-树查找操作的效率主要取决于查找过程中的外存访问次数。

与BST类似，B-树的每一次查找过程中，在每一高度上至多访问一个节点，即对于高度为h的B-树，外存访问不超过$O(h-1)$。B-树节点的分支数并不固定，故其高度h并不完全取决于树中关键码的总数n，对于包含N个关键码的m阶B-树，高度h的取值范围为：

$$\log_m(N+1)\le h \le \log_{\lceil m/2 \rceil} \lfloor(N+1)/2 \rfloor+1$$

也就是说，存有N个关键码的m阶B-树的高度$h=\Theta(\log_m N)$。因此每次查找过程共需访问$\Theta(\log_m N)$个节点，相应地需要做$\Theta(\log_m N)$次外存读取操作，因此对存有N个关键码的m阶B-树的每次查找操作，耗时不超过$\Theta(\log_m N)$。

尽管没有渐进意义上的改进，但相对而言极其耗时的I/O操作的次数，却已大致缩减为原来的$1/ \log_2 m$。鉴于m通常取值在256至1024之间，较之此前大致降低一个数量级，故使用B-树后，实际的访问效率将十分可观的提高。

2.3.关键码插入

为在B -树中插入一个新的关键码e，首先调用search(e)在树中查找该关键码。若查找成功，则按照“禁止重复关键码”的约定不予插入，操作完成并返回false。

否则查找过程必然终止于某一外部节点v，且其父节点由变量_hot指示，此时的 _hot必然指向某一叶节点。接下来在该节点中再次查找目标关键码e，这次查找是失败的但是可以确定e在其中的正确插入位置r，最后只需将e插至这一位置。

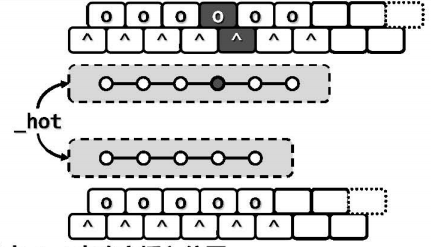
B-树的关键码插入算法实现如下：

template <typename T> bool BTree<T>::insert ( const T& e ) { //将关键码e插入B树中
   BTNodePosi(T) v = search ( e ); if ( v ) return false; //确认目标节点不存在
   Rank r = _hot->key.search ( e ); //在节点_hot的有序关键码向量中查找合适的插入位置
   _hot->key.insert ( r + 1, e ); //将新关键码插至对应的位置
   _hot->child.insert ( r + 2, NULL ); //创建一个空子树指针
   _size++; //更新全树规模
   solveOverflow ( _hot ); //如有必要，需做分裂
   return true; //插入成功
}

至此，_hot所指的节点中增加了一个关键码。若该节点关键码的总数依然合法（$\le m-1$），则插入操作随机完成；否则称该节点发生了一次上溢（overflow），此时需要适当的处理，使该节点以及整数重新满足B-树的条件。

上溢与分裂：

一般地，刚发生上溢的节点，应恰好含有m个关键码，若取$s=\lfloor m/2 \rfloor$，则它们依次为：

$$\{k_0,\dots,k_{s-1};\,k_s;\,k_{s+1},\dots,k_{m-1}\}$$

以$k_s$为界，可将该节点分为前、后两个字节点，且二者大致等长。可令关键码k上升一层，归入其父节点（若存在）中的适当位置，并分别以这两个子节点作为其左、右孩子，这一过程称作节点的分裂（split）。可以验证如此分裂所得的两个孩子节点，均符合m阶B-树关于节点分支数的条件。

可能的情况：

被提升的关键码，可能有三种进一步的处置方式。

首先如图(a1)，设原上溢节点的父亲节点存在，且足以接纳一个关键码。此种情况下，只需将被提升的关键码(37)按次序插入父节点中，修复即告完成，修复后的局部如图(a2)。

其次如图(b1)，尽管上溢节点的父节点存在，但也已处于饱和状态。此时如图(b2)，将被提升的关键码插入父节点之后，会导致父节点也发生上溢，这种现象称作上溢的向上传递。每经过一次修复，上溢节点的高度必然上升一层，最远不至超过树根。

最后如图(c1)，若上溢传递至树根节点，则可令被提升的关键码(37)自成一个节点，并作为新的树根，如图(c2)，至此上溢修复完毕，全树增高一层。这样新创建的树根仅含关键码，这也正是就B-树节点分支数的下限要求而言，树根节点作为例外的原因。

可见整个过程中所作分裂操作的次数，必不超过全树的高度，即$O(\log_m N)$。

针对上溢的处理算法实现如下：

template <typename T> //关键码插入后若节点上溢，则做节点分裂处理
void BTree<T>::solveOverflow ( BTNodePosi(T) v ) {
   if ( _order >= v->child.size() ) return; //递归基：当前节点并未上溢
   Rank s = _order / 2; //轴点（此时应有_order = key.size() = child.size() - 1）
   BTNodePosi(T) u = new BTNode<T>(); //注意：新节点已有一个空孩子
   for ( Rank j = 0; j < _order - s - 1; j++ ) { //v右侧_order-s-1个孩子及关键码分裂为右侧节点u
      u->child.insert ( j, v->child.remove ( s + 1 ) ); //逐个移动效率低
      u->key.insert ( j, v->key.remove ( s + 1 ) ); //此策略可改进
   }
   u->child[_order - s - 1] = v->child.remove ( s + 1 ); //移动v最靠右的孩子
   if ( u->child[0] ) //若u的孩子们非空，则
      for ( Rank j = 0; j < _order - s; j++ ) //令它们的父节点统一
         u->child[j]->parent = u; //指向u
   BTNodePosi(T) p = v->parent; //v当前的父节点p
   if ( !p ) { _root = p = new BTNode<T>(); p->child[0] = v; v->parent = p; } //若p空则创建之
   Rank r = 1 + p->key.search ( v->key[0] ); //p中指向u的指针的秩
   p->key.insert ( r, v->key.remove ( s ) ); //轴点关键码上升
   p->child.insert ( r + 1, u );  u->parent = p; //新节点u与父节点p互联
   solveOverflow ( p ); //上升一层，如有必要则继续分裂——至多递归O(logn)层
}

复杂度：

若将B-树的阶次m视作常数，则关键码的移动和复制操作所需的时间都可以忽略。而solveOverflow()算法其中的每一递归实例均只需常数时间，递归层数不超过B-树高度。由此可知，对于存有N个关键码的m阶B-树，每次插入操作都可在$O(\log_m N)$时间内完成。

实际上，因插入操作而导致$\Omega(\log_m N)$次分裂的情况极为罕见，单次插入操作平均引发的分裂次数，远远低于这一估计，故时间通常主要消耗于对目标关键码的查找。

2.4.关键码删除

为从B-树中删除关键码e，也首先需要调用search(e)查找e所属的节点。若查找失败，则说明关键码e尚不存在，删除操作即告完成；否则按照代码的出口约定，目标关键码所在的节点必由返回的位置v指示。此时，通过顺序查找，即可进一步确定e在节点 v中的秩r。

不妨假定v是叶节点，否则，e的直接后继（前驱）在其右（左）子树中必然存在，而且可在$O(height(v))$时间内确定它们的位置，其中$height(v)$为节点v的高度。此处不妨选用直接后继，于是e的直接后继关键码所属的节点u必为叶节点，且该关键码就是其中的最小者u[0]，然后令e与u[0]互换位置，即可确保删除的关键码e所属的节点是叶节点。

接下来可直接将e从v中删除，节点v中所含的关键码以及（空）分支将分别减少一半。此时，若该节点所含关键码的总数依然合法（$\ge \lceil m/2 \rceil-1$），则删除操作随机完成。否则，称该节点发生了下溢（underflow），并需要通过适当的处置，使该节点以及整数重新满足B-树的条件。

B-树的关键码删除算法的实现如下：

template <typename T> bool BTree<T>::remove ( const T& e ) { //从BTree树中删除关键码e
   BTNodePosi(T) v = search ( e ); if ( !v ) return false; //确认目标关键码存在
   Rank r = v->key.search ( e ); //确定目标关键码在节点v中的秩（由上，肯定合法）
   if ( v->child[0] ) { //若v非叶子，则e的后继必属于某叶节点
      BTNodePosi(T) u = v->child[r+1]; //在右子树中一直向左，即可
      while ( u->child[0] ) u = u->child[0]; //找出e的后继
      v->key[r] = u->key[0]; v = u; r = 0; //并与之交换位置
   } //至此，v必然位于最底层，且其中第r个关键码就是待删除者
   v->key.remove ( r ); v->child.remove ( r + 1 ); _size--; //删除e，以及其下两个外部节点之一
   solveUnderflow ( v ); //如有必要，需做旋转或合并
   return true;
}

下溢与合并：

由上，在m阶B-树中，刚发生下溢的节点V必恰好包含$\lceil m/2 \rceil-2$个关键码和$\lceil m/2 \rceil-1$个分支。一下将根据其左、右兄弟所含关键码的数目，分三种情况做相应的处置。

• v的左兄弟L存在，且至少包含$\lceil m/2 \rceil$个关键码：

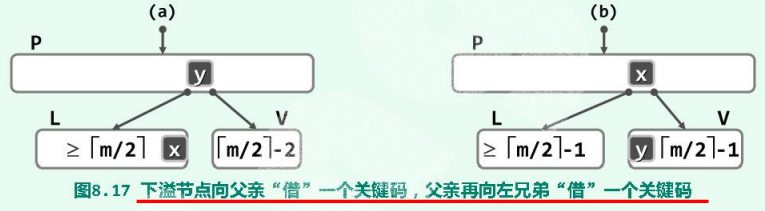
如图，不妨设L和V分别是其父节点P中关键码v的左、右孩子，L中最大关键码为x(x $\le$ y)。再将y从节点P转移至节点V中（作为最小关键码），再将x从L转移至P中（取代原关键码y）。至此，局部乃至整数都重新满足B-树条件，下溢修复完毕。

• v的左兄弟R存在，且至少包含$\lceil m/2 \rceil$个关键码：

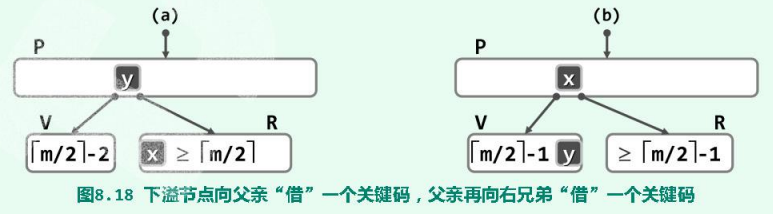
与第一种情况对称。

• V的左、右兄弟L和R或者不存在，或者其包含的关键码均不足$\lceil m/2 \rceil$个：

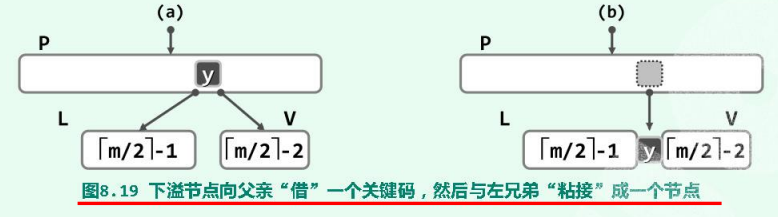
实际上，此时的L和R不可能同时存在。如图，不失一般性地设做兄弟节点L存在。当然，此时节点L恰好包含$\lceil m/2 \rceil-1$个关键码。

于是为修复节点V的下溢缺陷，如图(b)从父亲节点P中抽出介于L和V之间的关键码y，并通过该关键码将节点L和V“粘接”成一个节点——这一过程称作节点的合并（merge）。要注意的是，在经如此合并而得新节点中，关键码总数应为：

$$(\lceil m/2 -1 \rceil)+1+(\lceil m/2-2\rceil)=2\times \lceil m/2 \rceil-2\le m-1$$

故原节点V的下溢缺陷得以修复，而且不致于引发上溢。

接下来，还须检查父节点P——关键码y的删除可能致使该节点出现下溢，这种现象称作下溢的传递，可以通过套用上述三种方法来解决。特别地，当下溢传递至根节点且其中不再含有任何关键码时，即可将其删除并代之以其唯一的孩子节点，全树高度也随之下降一层。

整个下溢修复的过程至多需做$O(\log_m N)$次节点合并操作。

针对下溢的处理算法实现如下：

template <typename T> //关键码删除后若节点下溢，则做节点旋转或合并处理
void BTree<T>::solveUnderflow ( BTNodePosi(T) v ) {
   if ( ( _order + 1 ) / 2 <= v->child.size() ) return; //递归基：当前节点并未下溢
   BTNodePosi(T) p = v->parent;
   if ( !p ) { //递归基：已到根节点，没有孩子的下限
      if ( !v->key.size() && v->child[0] ) {
         //但倘若作为树根的v已不含关键码，却有（唯一的）非空孩子，则
         /*DSA*/printf ( "collapse\n" );
         _root = v->child[0]; _root->parent = NULL; //这个节点可被跳过
         v->child[0] = NULL; release ( v ); //并因不再有用而被销毁
      } //整树高度降低一层
      return;
   }
   Rank r = 0; while ( p->child[r] != v ) r++;
   //确定v是p的第r个孩子——此时v可能不含关键码，故不能通过关键码查找
   //另外，在实现了孩子指针的判等器之后，也可直接调用Vector::find()定位
   /*DSA*/printf ( "\nrank = %d", r );
// 情况1：向左兄弟借关键码
   if ( 0 < r ) { //若v不是p的第一个孩子，则
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      if ( ( _order + 1 ) / 2 < ls->child.size() ) { //若该兄弟足够“胖”，则
         /*DSA*/printf ( " ... case 1\n" );
         v->key.insert ( 0, p->key[r - 1] ); //p借出一个关键码给v（作为最小关键码）
         p->key[r - 1] = ls->key.remove ( ls->key.size() - 1 ); //ls的最大关键码转入p
         v->child.insert ( 0, ls->child.remove ( ls->child.size() - 1 ) );
         //同时ls的最右侧孩子过继给v
         if ( v->child[0] ) v->child[0]->parent = v; //作为v的最左侧孩子
         return; //至此，通过右旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，左兄弟要么为空，要么太“瘦”
// 情况2：向右兄弟借关键码
   if ( p->child.size() - 1 > r ) { //若v不是p的最后一个孩子，则
      BTNodePosi(T) rs = p->child[r + 1]; //右兄弟必存在
      if ( ( _order + 1 ) / 2 < rs->child.size() ) { //若该兄弟足够“胖”，则
         /*DSA*/printf ( " ... case 2\n" );
         v->key.insert ( v->key.size(), p->key[r] ); //p借出一个关键码给v（作为最大关键码）
         p->key[r] = rs->key.remove ( 0 ); //ls的最小关键码转入p
         v->child.insert ( v->child.size(), rs->child.remove ( 0 ) );
         //同时rs的最左侧孩子过继给v
         if ( v->child[v->child.size() - 1] ) //作为v的最右侧孩子
            v->child[v->child.size() - 1]->parent = v;
         return; //至此，通过左旋已完成当前层（以及所有层）的下溢处理
      }
   } //至此，右兄弟要么为空，要么太“瘦”
// 情况3：左、右兄弟要么为空（但不可能同时），要么都太“瘦”——合并
   if ( 0 < r ) { //与左兄弟合并
      /*DSA*/printf ( " ... case 3L\n" );
      BTNodePosi(T) ls = p->child[r - 1]; //左兄弟必存在
      ls->key.insert ( ls->key.size(), p->key.remove ( r - 1 ) ); p->child.remove ( r );
      //p的第r - 1个关键码转入ls，v不再是p的第r个孩子
      ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
      if ( ls->child[ls->child.size() - 1] ) //v的最左侧孩子过继给ls做最右侧孩子
         ls->child[ls->child.size() - 1]->parent = ls;
      while ( !v->key.empty() ) { //v剩余的关键码和孩子，依次转入ls
         ls->key.insert ( ls->key.size(), v->key.remove ( 0 ) );
         ls->child.insert ( ls->child.size(), v->child.remove ( 0 ) );
         if ( ls->child[ls->child.size() - 1] ) ls->child[ls->child.size() - 1]->parent = ls;
      }
      release ( v ); //释放v
   } else { //与右兄弟合并
      /*DSA*/printf ( " ... case 3R\n" );
      BTNodePosi(T) rs = p->child[r + 1]; //右兄弟必存在
      rs->key.insert ( 0, p->key.remove ( r ) ); p->child.remove ( r );
      //p的第r个关键码转入rs，v不再是p的第r个孩子
      rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
      if ( rs->child[0] ) rs->child[0]->parent = rs; //v的最左侧孩子过继给ls做最右侧孩子
      while ( !v->key.empty() ) { //v剩余的关键码和孩子，依次转入rs
         rs->key.insert ( 0, v->key.remove ( v->key.size() - 1 ) );
         rs->child.insert ( 0, v->child.remove ( v->child.size() - 1 ) );
         if ( rs->child[0] ) rs->child[0]->parent = rs;
      }
      release ( v ); //释放v
   }
   solveUnderflow ( p ); //上升一层，如有必要则继续分裂——至多递归O(logn)层
   return;
}

复杂度：

与插入操作同理，在存有N个关键码的m阶B-树中的每次关键码删除操作，都可以在$O(\log_m N)$时间内完成。另外同样地，因某一关键码的删除而导致$\Omega(\log_m N)$次合并操作的情况也极为罕见，单词删除操作过程中平均只需做常数次节点的合并。