数据结构与算法（19）优先级队列

[TOC]

此前的搜索树结构和词典结构，都支持覆盖数据全集的访问和操作，其中存储的每一数据对象都可作为查找和访问目标，为此搜索树结构需要在所有元素之间定义并维护一个显式的全序关系。优先级队列，这类结构则将操作对象限定于当前的全局极值者。这种根据数据对象之间相对优先级对其进行访问的方式，称作循优先级访问（call-by-priority）。

“全局极值”隐含了“所有元素可相互比较”这一性质，但优先级队列并不会也不必动态维护这个全序，却转而维护一个偏序（partial order）关系，如此不仅足以高效地支持仅针对极值对象的接口操作，更可有效地控制整体计算成本。作为不失高效率的轻量数据结构，对于常规的查找、插入或删除操作，优先级队列的效率并不低于此前的结构；而对于数据集的批量构建及相互合并等操作，其性能却更胜一筹。

1.接口定义

除了作为存放数据的容器，数据结构还应能够按某种约定的次序动态地组织数据，以支持高效的查找和修改操作，如遵循“先进先出”原则的队列，而有些实际情况则要按某种优先级原则，如医院抢救最危急的病人。

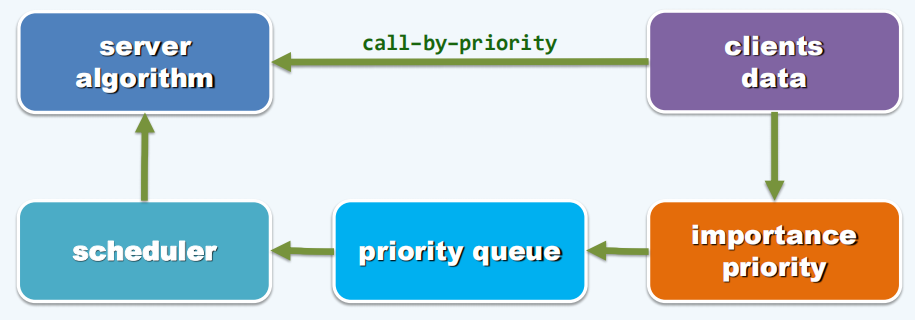
从数据结构的角度看，无论是待排序节点的数值、超字符的权重，还是时间的发生时间，数据项的某种属性只要可以相互比较大小，则这种大小关系即可称作优先级（priority）。而按照事先约定的优先级，可以始终高效查找并访问优先级最高数据项的数据结构，也统称作优先级队列（priority queue）。

仿照词典结构，也讲优先级队列中的数据项称作词条（entry），而与特定优先级相对应的数据属性，也称作关键码（key）。作为确定词条优先级的依据，关键码之间必须可以比较大小（词典结构仅要求关键码支持判等操作）。因此对于优先级队列，必须以比较器的形式兑现对应的优先级关系，为了简化起见，这里假定关键码或者可直接比较，或者已重载了对应的操作符。

优先级队列作为一类独特数据的意义恰恰在于，通过转而维护词条的一个偏序关系，不仅依然可以支持对最高优先级词条的动态访问，而且可将相应的计算成本控制在足以令人满意的范围之内。

优先级队列接口的定义如下表：

操作接口	功能描述
size()	报告优先级队列的规模，即其中词条的总数
insert()	将指定词条插入优先级队列
getMax()	返回优先级最大的词条（若优先级队列非空）
delMax()	删除优先级最大的词条（若优先级队列非空）

这里以模板类PQ的形式给出优先级队列的操作接口定义，这一组基本的ADT接口可能有不同的实现方式，故这里均以虚函数形式统一描述这些接口，以便在不同的派生类中具体实现。

template <typename T> struct PQ { //优先级队列PQ模板类
   virtual void insert ( T ) = 0; //按照比较器确定的优先级次序插入词条
   virtual T getMax() = 0; //取出优先级最高的词条
   virtual T delMax() = 0; //删除优先级最高的词条
};

2.实现

2.1.尝试

考虑用此前学过的数据结构来实现优先级队列，要兼顾efficiency和cost，以下考虑了向量Vector，有序向量Sorted Vector，列表List，有序列表Sorted List和平衡二叉搜索树BBST，但基于它们实现的优先级队列都不能实现高效率和低cost的兼顾。

Vector:

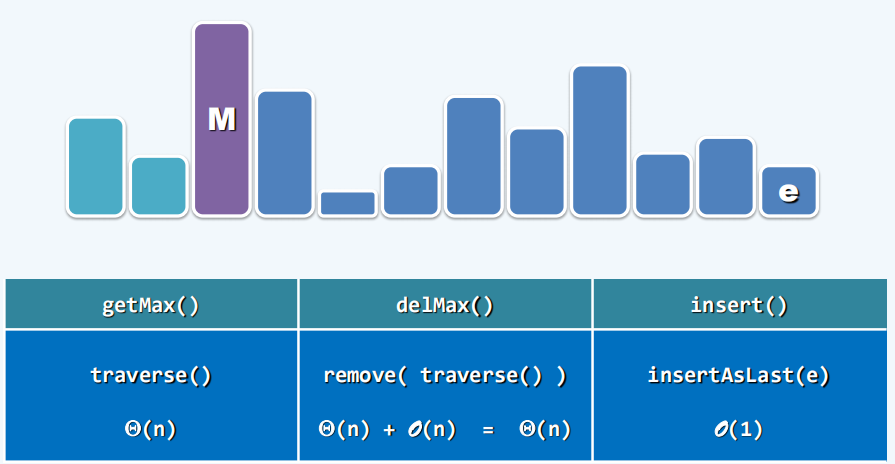
Sorted Vector：

List：

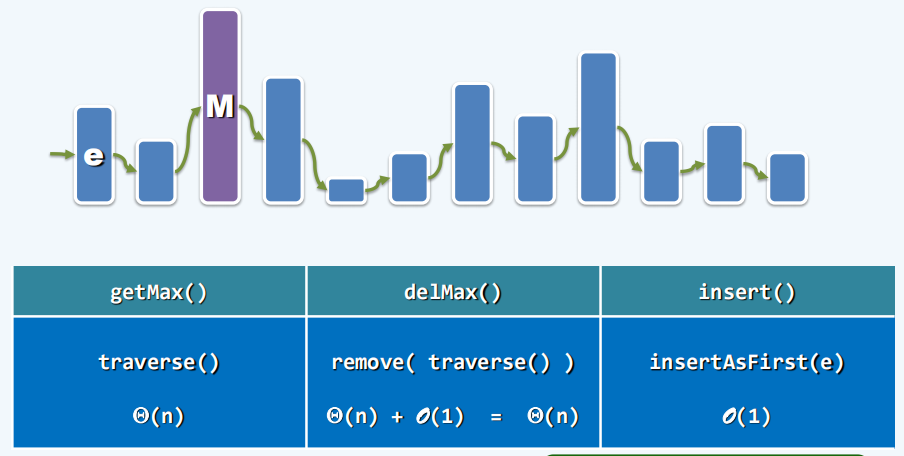
Sorted List：

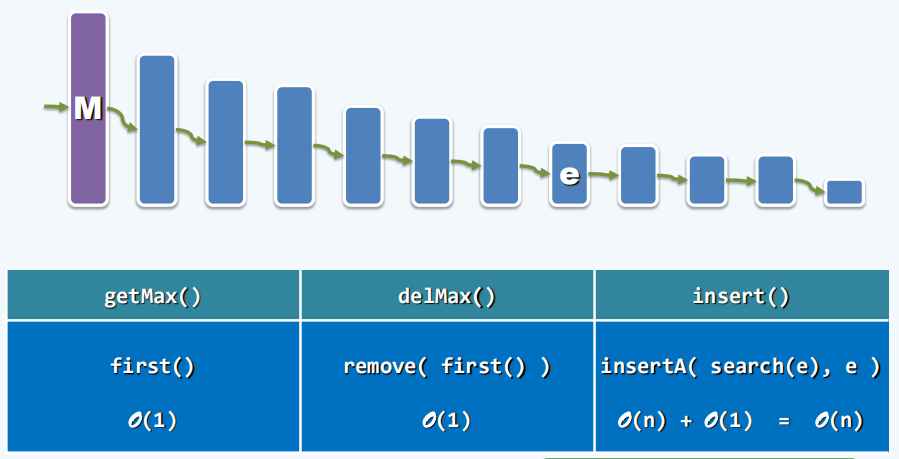
BBST：

对于AVL、Splay、Red-black这三种数据结构，查找、插入和删除三个接口均只需$O(\log n)$时间，但是BBST的功能却远远超出了PQ的需求，可以这么理解：

$$PQ=1\times insert()+0.5\times search()+0.5\times remove()=\frac{2}{3}\times BBST$$

若只需查找极单元，则不必维护所有元素之间的全序关系，偏序足矣，因此有理由相信，存在某种更为简单、维护成本更低的实现方式，使得各功能接口时间复杂度依然为$O(\log n)$，而且实际效率更高。

2.2.完全二叉堆

有限偏序的极值必然存在，借助堆（heap）结构可以维护一个偏序，堆有多种实现形式，这里采用一种最基本的形式——完全二叉堆（complete binary heap），它具有结构性与堆序性。

结构性：其逻辑结构等同于完全二叉树（complete binary tree），即平衡因子处处非负（只能是0或1）的AVL树。因此由n个词条组成的完全二叉堆的高度$h=\lfloor \log_2 n \rfloor=O(\log n)$。

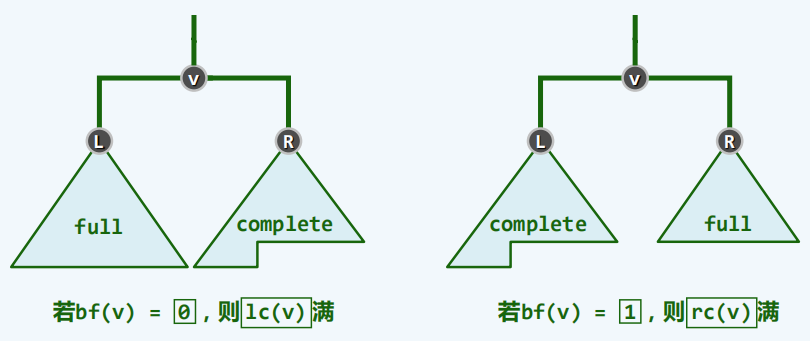
堆序性：堆顶以外的每个节点都不大于其父节点，称为大顶堆；还可定义为堆顶以外的每个节点都不小于其父节点，称为小顶堆。

尽管二叉树不属于线性结构，但作为特例的完全二叉树，却与向量有着紧密的对应关系。完全二叉堆的拓扑联接结构，完全由其规模n确定。按照层次遍历的次序，每个节点都对应于唯一的编号。故若将所有节点组织为一个向量，则堆中所有节点（编号）与向量各单元（秩）也将彼此一一对应。

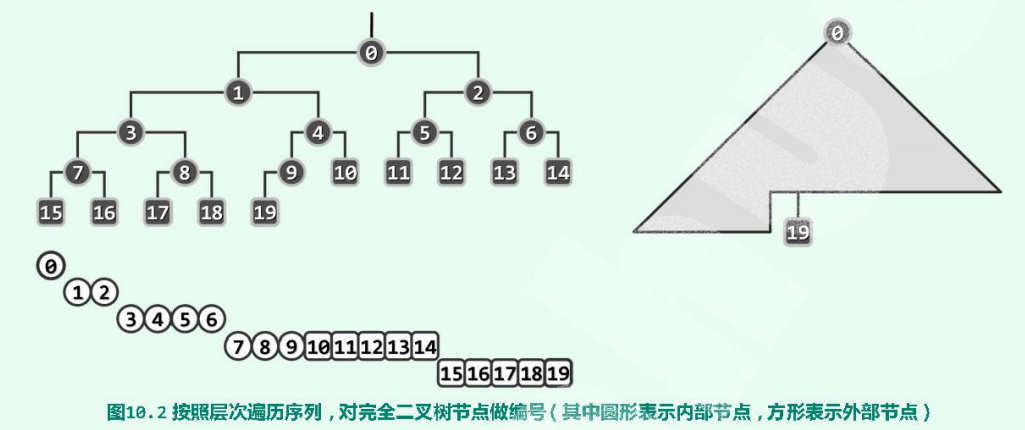
这一实现方式的优势首先体现在，各节点在物理上连续排列，故总共仅需$O(n)$空间，而且更重要的是，利用各节点的编号（或秩），也可便捷地判别父子关系，对于任意节点v，必然满足：

• 若v有左孩子，则$i (lchild(v))=2*i(v)+1$;
• 若v有右孩子，则$i (rchild(v))=2*i(v)+2$;
• 若v有父节点，则$i(parent(v))=\lfloor(i(v)-1)/2\rfloor=\lceil i(v)/2)\rceil-1$

最后，由于向量支持低分摊成本的扩容调整，故随着堆的 规模和内容不断地动态调整，除标准接口以外的操作所需的时间可以忽略不计。

2.3.实现

宏：为简化后续算法的描述及实现，可如下代码所示预先设置一系列的宏定义。

#define  Parent(i)         ( ( ( i ) - 1 ) >> 1 ) //PQ[i]的父节点（floor((i-1)/2)，i无论正负）
#define  LChild(i)         ( 1 + ( ( i ) << 1 ) ) //PQ[i]的左孩子
#define  RChild(i)         ( ( 1 + ( i ) ) << 1 ) //PQ[i]的右孩子
#define  InHeap(n, i)      ( ( ( -1 ) < ( i ) ) && ( ( i ) < ( n ) ) ) //判断PQ[i]是否合法
#define  LChildValid(n, i) InHeap( n, LChild( i ) ) //判断PQ[i]是否有一个（左）孩子
#define  RChildValid(n, i) InHeap( n, RChild( i ) ) //判断PQ[i]是否有两个孩子
#define  Bigger(PQ, i, j)  ( lt( PQ[i], PQ[j] ) ? j : i ) //取大者（等时前者优先）
#define  ProperParent(PQ, n, i) /*父子（至多）三者中的大者*/ \
            ( RChildValid(n, i) ? Bigger( PQ, Bigger( PQ, i, LChild(i) ), RChild(i) ) : \
            ( LChildValid(n, i) ? Bigger( PQ, i, LChild(i) ) : i \
            ) \
            ) //相等时父节点优先，如此可避免不必要的

PQ_ComplHeap模板类：借助多重继承的机制，定义完全二叉堆模板类PQ_ComplHeap

#include "Vector/Vector.h" //借助多重继承机制，基于向量
#include "PQ/PQ.h" //按照优先级队列ADT实现的
template <typename T> struct PQ_ComplHeap : public PQ<T>, public Vector<T> { //完全二叉堆
   /*DSA*/friend class UniPrint; //演示输出使用，否则不必设置友类
   PQ_ComplHeap() { } //默认构造
   PQ_ComplHeap ( T* A, Rank n ) { copyFrom ( A, 0, n ); heapify ( _elem, n ); } //批量构造
   void insert ( T ); //按照比较器确定的优先级次序，插入词条
   T getMax(); //读取优先级最高的词条
   T delMax(); //删除优先级最高的词条
}; //PQ_ComplHeap
template <typename T> void heapify ( T* A, Rank n ); //Floyd建堆算法
template <typename T> Rank percolateDown ( T* A, Rank n, Rank i ); //下滤
template <typename T> Rank percolateUp ( T* A, Rank i ); //上滤

getMax()：既然全局优先级最高的词条总是位于堆顶，因此只需返回向量的首单元，即可在$O(1)$时间内完成getMax()操作。

template <typename T> T PQ_ComplHeap<T>::getMax() {  return _elem[0];  } //取优先级最高的词条

2.4.插入算法

插入算法首先要调用向量的标准插入接口，将新词条接至向量的末尾，得益于向量结构良好的封装性，这里无需关心这一步骤的具体细节，尤其是无需考虑溢出扩容等特殊情况。

新引入的词条并未破坏堆的结构性，但只要新词条e不是堆顶，就有可能与其父亲违反堆序性，而其他位置的堆序性依然满足，故以下将调用percolateUp()函数，对新接入的词条做适当调整，在保持结构性的前提下恢复整体的堆序性。

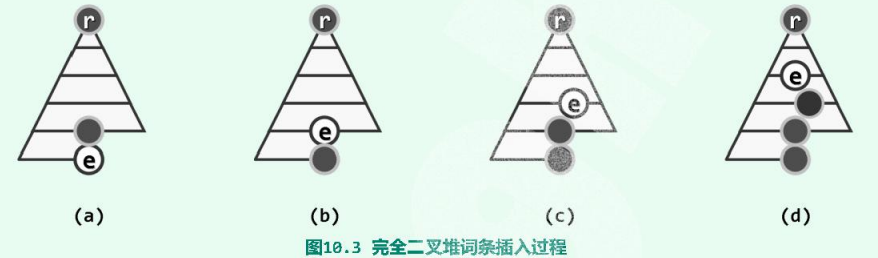
上滤：

根据e在向量中对应的秩，可以简便地确定词条p对应的秩，即$i(parent(v))=\lfloor(i(v)-1)/2\rfloor$。此时若经比较判定$e\le p$，则堆序性在此局部以至全堆均已满足，插入操作因此即告完成。反之，若$e>p$，则可在向量中令e和p互换位置。如此不仅全堆的结构性依然满足，而且e和p之间的堆序性也得以恢复。此后e与其新父亲，可能再次违背堆序性，只需继续套用以上方法。

每交换一次，新词条e都向上攀升一层，故这一过程也形象地称作上滤（percolate up），e至多上滤至堆顶，一旦上滤完成，全堆的堆序性必将恢复。下面是一个实例：

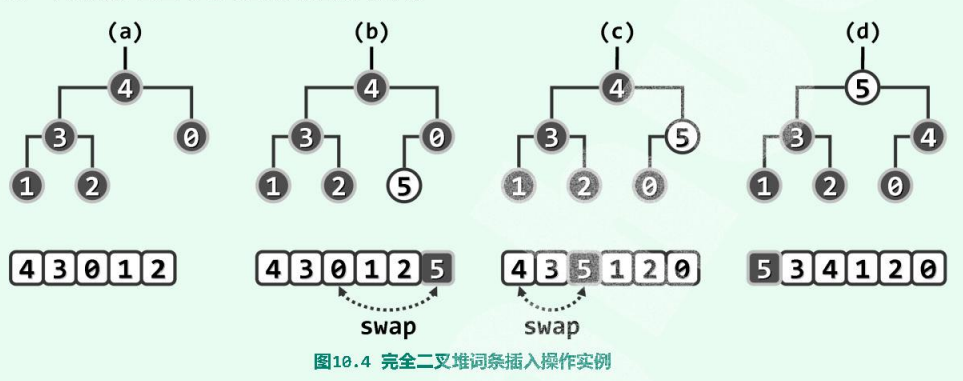
上滤调整过程中交换操作的累计次数，不致超过全堆的高度$\lfloor \log_2n \rfloor$，而在向量中，每次交换操作只需常数时间，故上滤调整乃至整个词条插入算法整体的时间复杂度，均为$O(\log n)$。

插入算法和上滤调整的代码实现如下：

template <typename T> void PQ_ComplHeap<T>::insert ( T e ) { //将词条插入完全二叉堆中
   Vector<T>::insert ( e ); //首先将新词条接至向量末尾
   percolateUp ( _elem, _size - 1 ); //再对该词条实施上滤调整
}

//对向量中的第i个词条实施上滤操作，i < _size
template <typename T> Rank percolateUp ( T* A, Rank i ) {
   while ( 0 < i ) { //在抵达堆顶之前，反复地
      Rank j = Parent ( i ); //考查[i]之父亲[j]
      if ( lt ( A[i], A[j] ) ) break; //一旦父子顺序，上滤旋即完成；否则
      swap ( A[i], A[j] ); i = j; //父子换位，并继续考查上一层
   } //while
   return i; //返回上滤最终抵达的位置
}

2.5.元素删除

待删除词条r总是位于堆顶，故可直接将其取出并备份，堆的结构性将破坏。为修复这一缺陷，将最末尾的词条e转移至堆顶。而新的堆顶可能与其孩子们违背堆序性——尽管其他位置的堆序性依然满足，故下调用percolateDown()函数调整新堆顶，在保持结构性的前提下，恢复整体的堆序性。

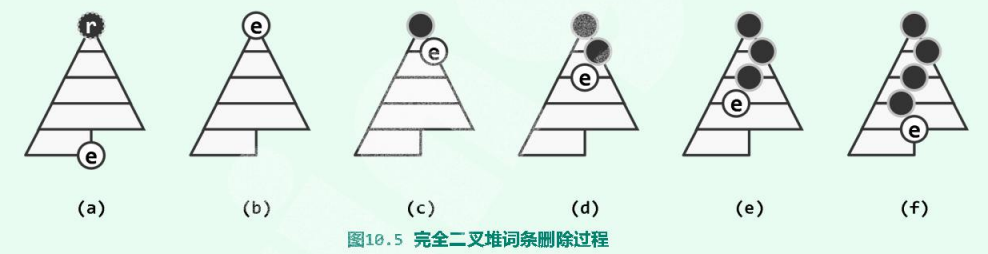
下滤：

若新堆顶e不满足堆序性，将e与其（至多）两个孩子中的大者交换位置。此后，堆中可能的缺陷依然只能来自与词条e——它与新孩子可能再次违背堆序性，只需继续套用以上方法。因每进过一次交换，词条e都会下降一层，故这一调整过程也称作下滤（percolate down）。与上滤同理，这一过程也必然终止，全堆的堆序性必将恢复，下滤乃至整个删除算法的时间复杂度也为$O(\log n)$。下面是一个实例：

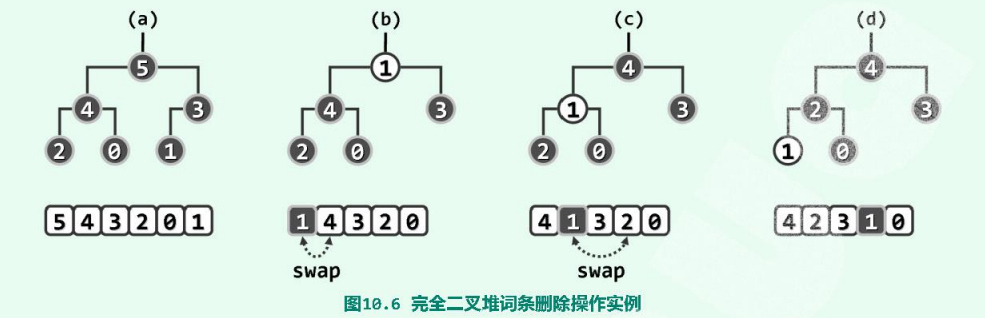
删除算法和下滤调整的代码实现如下：

template <typename T> T PQ_ComplHeap<T>::delMax() { //删除非空完全二叉堆中优先级最高的词条
   T maxElem = _elem[0]; _elem[0] = _elem[ --_size ]; //摘除堆顶（首词条），代之以末词条
   percolateDown ( _elem, _size, 0 ); //对新堆顶实施下滤
   return maxElem; //返回此前备份的最大词条
}

//对向量前n个词条中的第i个实施下滤，i < n
template <typename T> Rank percolateDown ( T* A, Rank n, Rank i ) {
   Rank j; //i及其（至多两个）孩子中，堪为父者
   while ( i != ( j = ProperParent ( A, n, i ) ) ) //只要i非j，则
      { swap ( A[i], A[j] ); i = j; } //二者换位，并继续考查下降后的i
   return i; //返回下滤抵达的位置（亦i亦j）
}

2.6.建堆

很多算法中输入词条都是成批给出，故在初始化阶段往往需要解决一个共同问题：给定一组词条，高效地将它们组织成一个堆，这一过程也称作“建堆”（heapification）。

蛮力算法：

从空堆起反复调用标准insert()接口，即可将词条逐一插入其中，并最终完成建堆。尽管这一方法无疑正确，但其消耗的时间却过多。具体地，若共有n个词条，则共需迭代n次，第k轮迭代耗时$O(\log k)$，故累计耗时时间量应为：

$$O(\log 1+\log 2+\dots +\log n)=O(\log n!)=O(n\log n)$$

如此多的时间本来足以将所有词条做全排序，而在这里花费同样多的时间所生成的堆却只能提供一个偏序，这也暗示了存在某种更快的建堆方法。

自上而下的上滤：

在将所有输入词条纳入长为n的向量之后，首单元处的词条本身即可视作一个规模为1的堆。接下来考查下一单元，只需调用percolateUp()对其上滤，此后前两单元将构成规模为2的堆，如此反复进行，直到最终得到规模为n的堆。

这一过程可归纳为：对任何一棵完全二叉树，只需自顶而下、自左向右地对其中每个节点实施一次上滤，即可使之成为完全二叉堆。在此过程中，为将每个节点纳入堆中，所需消耗的时间量将线性正比与该节点的深度。不妨考查高度为$h$、规模为$n=2^{h+1}-1$的满二叉树，其中高度为$i$的节点共有$2^i$个，因此整个算法的总体时间复杂度为：

$$\sum^h_{i=0}(i\cdot 2^i )=(d-1)\times 2^{d+1}+2=(\log_2(n+1)-2)\cdot (n+1)+2=O(n\log n)$$

Floyd算法（自下而上的下滤）：

考虑一个相对简单的问题：任给堆$H_0$和$H_1$，以及另一独立节点p，然后以p为中介将堆$H_0$和$H_1$合并，故称作堆合并操作。首先为满足结构性，可将这两个堆当作p的左、右子树，联接成一棵完整的二叉树。此时等效于在delMax()操作中摘除堆顶，再将末位词条（p）转移至堆顶，以下只需对p实施下滤操作，即可将全树转换为堆。

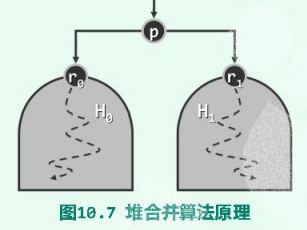
如果将以上过程作为实现堆合并的一个通用算法，则在将所有词条组织为一棵完全二叉树后，只需自底而上地反复套用这一算法，即可不断地将处于下层的堆逐对地合并成更高一层的堆，并最终得到一个完整的堆。按照这构思，即可实现Floyd建堆算法。下面是一个实例：

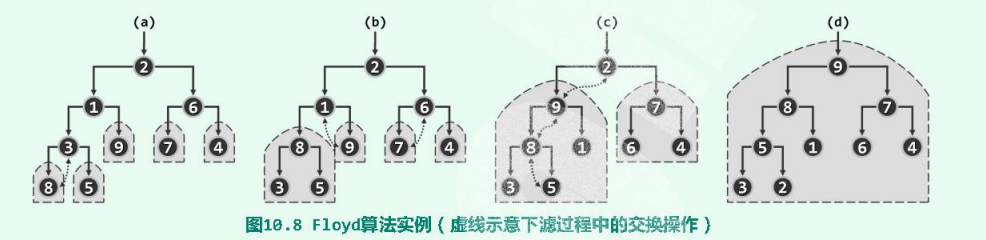
在前几节知识的基础上，Floyd算法的实现十分简洁：只需自下而上、由深而浅地遍历所有内部节点，并对每个内部节点分别调用一次下滤算法percolateDown()。

template <typename T> void heapify ( T* A, const Rank n ) { //Floyd建堆算法，O(n)时间
   for ( int i = n/2 - 1; 0 <= i; i-- ) //自底而上，依次
      percolateDown ( A, n, i ); //下滤各内部节点
}

复杂度：Floyd算法依然需要做n步迭代，以对所有节点各做一次下滤。这里每个节点的下滤所需的时间正比与其高度，故总体运行时间取决于各节点的高度总和。以高度为$h$，规模为$n=2^{h+1}-1$的满二叉树为例，其运行时间为：

$$\sum^h_{i=0}((d-i)\cdot 2^i)=2^{d+1}-(d+2)=n-\log_2(n+1)=O(n)$$

由于在遍历所有词条之前，绝不可能确定堆的结果，故以上已是建堆操作的最优算法。由此反观，蛮力算法低效率的根源，恰在于其“自上而下的下滤”策略。如此，各节点所消耗的时间线性正比于其深度——而在完全二叉树中，深度小的节点，远远少于高度小的节点。

2.7.就地堆排序

完全二叉堆有另一具体应用：对于向量中的n个词条，如何借助堆的相关算法，实现高效的排序，相应地这类算法也称作堆排序（heapsort）算法。既然此前归并排序算法的渐进复杂度已达到理论上最优的$O(n\log n)$，故这里将更关注与如何降低复杂度常系数。同时也希望空间复杂度能够有所降低，最好是除输入本身以外只需$O(1)$辅助空间。

原理：

算法的总体思路和策略与选择排序算法基本相同：将所有词条分成未排序和已排序两类，不断从前一类中取出最大者，顺序加至后一类中。这里不妨将其划分为前缀H和与之互补的后缀S，分别对应于上述未排序和已排序部分。新算法的不同之处在于：整个排序过程中，无论H包含多少词条，始终都组织为一个堆。另外，整个算法过程始终满足不变性：H中的最大词条不会大于S中的最小词条——除非二者之一为空，比如算法的初始和终止时刻。

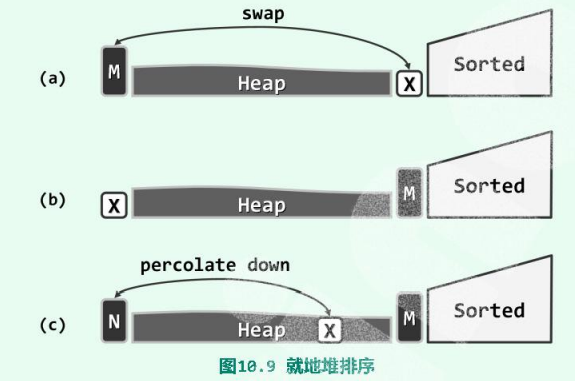
首先如图(a)，取出首单元词条M，将其与末单元词条X交换。M即是当前堆中的最大者，同时根据不变性也不大于S中的任何词条，故如此交换之后M必处于正确的排序位置。故如图(b)，此时可等效地认为S向前扩大了一个单元，H相应地缩小了一个单元，注意如此重新分界之后，H和S依然满足以上不变性。最后仿照此前的词条删除算法，只需对X实施一次下滤调整，即可使H整体的堆序性重新恢复，结果如图(c)。

复杂度：

在每一步迭代中，交换M和X只需常数时间，对X的下滤调整不超过$O(\log n)$时间，因此全部n步迭代累计耗时不超过$O(n\log n)$，再加上建堆所用时间，整个算法的运行时间也不超过$O(n\log n)$。纵览算法的整个过程，除了用于支持词条交换的一个辅助单元，几乎不需要更多的辅助空间，故的确属于就地算法。

得益于向量结构的简洁性，几乎所有以上操作都可便捷地实现，因此该算法不仅可简明地编码，其实际运行效率也因此往往要高于其他$O(n \log n)$的算法，这离不开堆这一精巧的数据结构。

实例：

以向量$\{4,2,5,1,3\}$的堆排序过程为例，首先采用Floyd算法将该向量整理为一个完全二叉堆，其中虚线示意下滤过程中的词条交换操作。

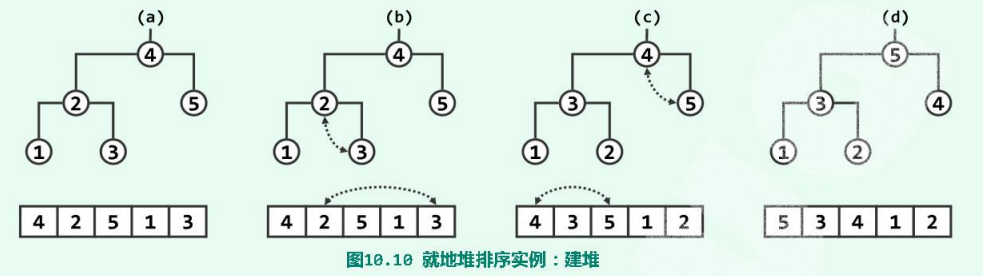
然后按照堆排序算法只需5步迭代，完成排序。

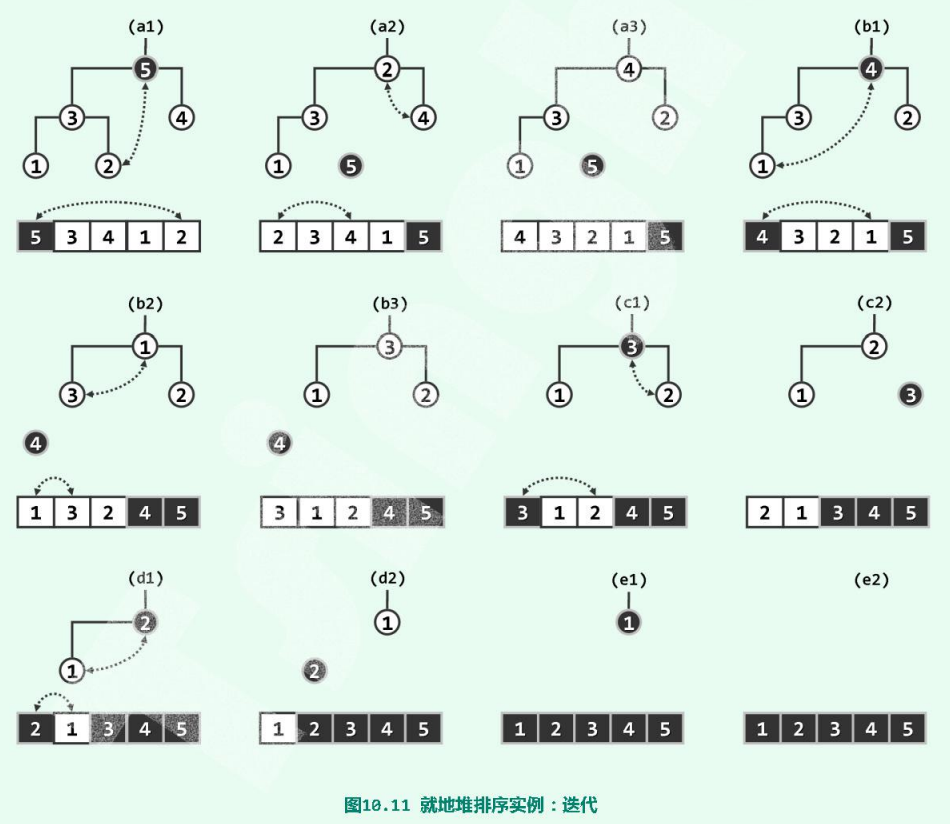
实现：

template <typename T> void Vector<T>::heapSort ( Rank lo, Rank hi ) { //0 <= lo < hi <= size
   PQ_ComplHeap<T> H( _elem + lo, hi - lo );  //将待排序区间建成一个完全二叉堆，O(n)
   while ( !H.empty() ) //反复地摘除最大元并归入已排序的后缀，直至堆空
      _elem[--hi] = H.delMax();  //等效于堆顶与末元素对换后下滤
}

3.左式堆

3.1.堆合并

除了标准的插入和删除操作，堆结构在实际应用中的另一常见操作即为合并，即任给堆A和堆B，如何将二者所含的词条组织为一个堆。

可以想到两种简单的方法：一是反复取出堆B的最大词条并插入堆A中，将两堆的规模分别记为n和m，且$n\ge m$，每一步迭代均需要做一次删除操作和一次插入操作，分别耗时$O(\log m)$和$O(\log(n+m))$，共需m步迭代，故总体运行时间应为：

$$m\times [O(\log m)+O(\log(n+m))]=O(m\log(n+m))=O(m\log n)$$

另一种是将两个堆中的词条视作彼此独立的对象，从而可以借助Floyd算法，将它们组织为一个新的堆H，运行时间为：

$$O(n+m)=O(n)$$

尽管其性能梢优于前一个，但仍无法令人满意。实际上，既然所有词条已分两组各自成堆，则意味着它们已经具有一定的偏序性，这样构建一个更大的偏序集，理应比由一组相互独立的词条构建偏序集更为容易。以上尝试均未奏效的原因在于，不能保证合并操作所涉及的节点足够少。为此不妨设想，堆是否也必须与二叉搜索树一样，尽可能地保持平衡？而对于堆来说，为控制合并操作所涉及的节点数，反而需要保持某种意义上的“不平衡”。

3.2.单侧倾斜

左式堆（leftist heap）是优先级队列的另一实现方式，可高效地支持堆合并操作。其基本思路是：在保持堆序性的前提下附加新的条件，使得在堆的合并过程中，只需调整很少量的节点。具体地，需参与调整的节点不超过$O(\log n)$个，故可达到极高的效率。

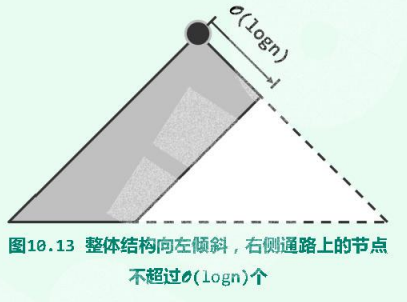
左式堆的整体结构呈单侧倾斜状，其中节点的分布均偏向左侧，左式堆将不再如完全二叉堆那样满足结构性。这也不难理解，毕竟堆序性才是堆结构的关键条件，而结构性只不过是堆的一项附加条件。在将平衡性替换为左倾性之后，左式堆结构的merge()操作乃至insert()和delMax()操作均可高效地实现。

按照以上思路，可借助多重继承的机制，定义左式堆模板类PQ_LeftHeap：

#include "PQ/PQ.h" //引入优先级队列ADT
#include "BinTree/BinTree.h" //引入二叉树节点模板类

template <typename T>
class PQ_LeftHeap : public PQ<T>, public BinTree<T> { //基于二叉树，以左式堆形式实现的PQ
   /*DSA*/friend class UniPrint; //演示输出使用，否则不必设置友类
public:
   PQ_LeftHeap() { } //默认构造
   PQ_LeftHeap ( T* E, int n ) //批量构造：可改进为Floyd建堆算法
   {  for ( int i = 0; i < n; i++ ) insert ( E[i] );  }
   void insert ( T ); //按照比较器确定的优先级次序插入元素
   T getMax(); //取出优先级最高的元素
   T delMax(); //删除优先级最高的元素
}; //PQ_LeftHeap

PQ_LeftHeap模板类借助多重继承机制，由PQ和BinTree结构共同派生而得。既然左式堆的逻辑结构不再等价于完全二叉树，若沿用此前基于向量的实现方法，必将难以控制空间复杂度。因此改用紧凑型稍差，灵活性更强的二叉树结构，将更具针对性。

3.3.空节点路径长度

为控制左式堆的倾斜度，可借鉴AVL树和红黑树的技巧，先引入外部节点，将结构转化为真二叉树，然后为各节点引入“ 空节点路径长度 ”指标，并依此确定相关算法的执行方向。节点x的空节点路径长度（null path length），即做npl(x)。若x为外部节点，则约定npl(x) = npl(null) = 0。反之若x为内部节点，则npl(x)可递归地定义为：npl(x) = 1 + min( npl( lc(x) ), npl( rc(x) ) )，即节点x的npl值取决于其左、右孩子npl值中的小者。

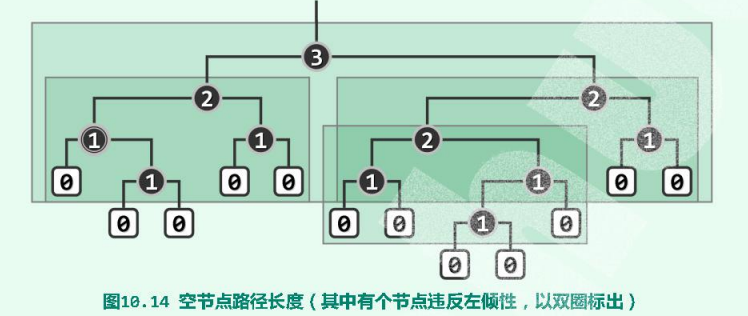
不难验证：npl(x)既等于x到外部节点的最近距离，同时也等于以x为根的最大满子树的高度。

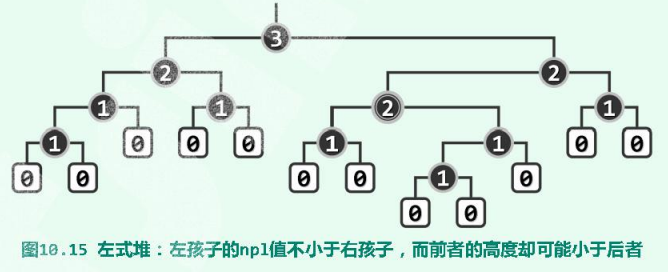
左式堆是处处满足“ 左倾性 ”的二叉堆，即任一内部节点x都满足：npl( lc(x) ) $\ge$ npl( rc(x) )，即就npl指标而言，任一内部节点的左孩子都不小于其右孩子。

由npl及左倾性的定义可以发现，左式堆中任一内节点x都应满足：npl(x) = 1 + npl( rc(x) )，即左式堆中每个节点的npl值，仅取决于其右孩子。要注意的是，“ 左孩子的npl值不小于右孩子 ”并不意味着 “ 左孩子的高度比不小于右孩子 ”。

3.4.最右侧通路

从x出发沿右侧分支一直前行直至空节点，经过的通路称作最右侧通路（rightmost path），记作rPath(x)。在左式堆中，尽管右孩子高度可能大于左孩子，但由“ 各节点npl值均决定于其右孩子 ”这一事实不难发现，每个节点的npl值，应恰好等于其最右侧通路的长度。

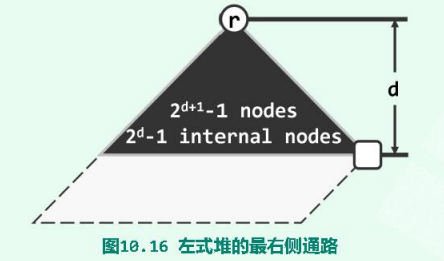
根节点r的最右侧通路，在此扮演的角色极其重要，rPath(r)的终点必为全堆中深度最小的外部节点，若记：npl(r) = |rPath(r)| = d，则该堆应包含一棵以r为根，高度为d的满二叉树（黑色部分），且该满二叉树至少应包含$2^{d+1}-1$个节点、$2^d-1$个内部节点——这也是堆的规模下限；反之在包含n个节点的左式堆中，最右侧通路必然不会长于：$\lfloor \log_2(n+1) \rfloor-1=O(\log n)$。

3.5.合并算法

假设待合并的左式堆分别以a和b为堆顶，且不失一般性地令$a\ge b$。于是可递归地将a的右子堆$a_R$与堆b合并，然后作为节点a的右孩子替换原先的$a_R$。为保证依然满足左倾性条件，最后还需要比较a左、右孩子的npl值——如有必要还需将二者交换，以保证左孩子的npl值不低于右孩子。

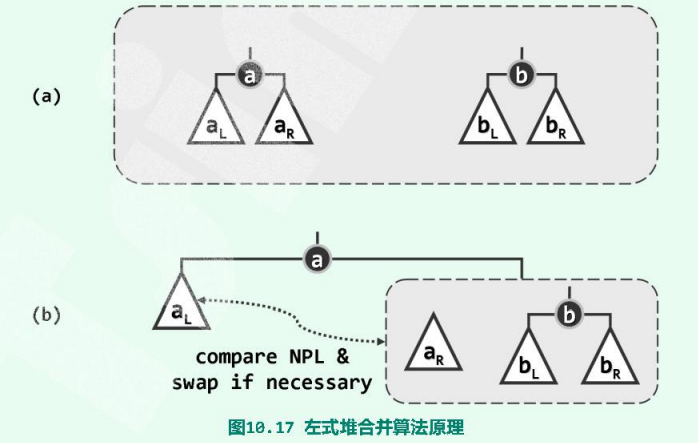
下面是一个实例：

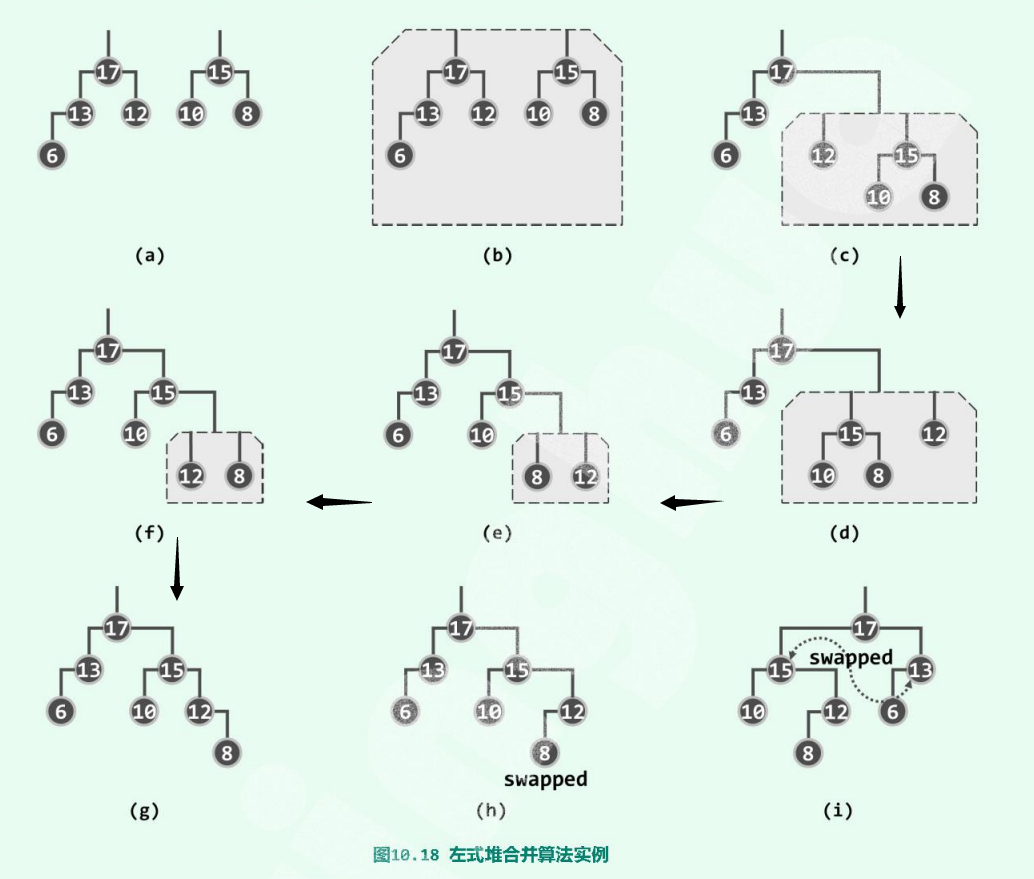
按照以上思路，左式堆合并算法可实现为如下的代码：

template <typename T> //根据相对优先级确定适宜的方式，合并以a和b为根节点的两个左式堆
static BinNodePosi(T) merge ( BinNodePosi(T) a, BinNodePosi(T) b ) {
   if ( ! a ) return b; //退化情况
   if ( ! b ) return a; //退化情况
   if ( lt ( a->data, b->data ) ) swap ( a, b ); //一般情况：首先确保b不大
   ( a->rc = merge ( a->rc, b ) )->parent = a; //将a的右子堆，与b合并
   if ( !a->lc || a->lc->npl < a->rc->npl ) //若有必要
      swap ( a->lc, a->rc ); //交换a的左、右子堆，以确保右子堆的npl不大
   a->npl = a->rc ? a->rc->npl + 1 : 1; //更新a的npl
   return a; //返回合并后的堆顶
} //本算法只实现结构上的合并，堆的规模须由上层调用者负责更新

复杂度：

以上的合并算法中，所有递归实例可排成一个线性序列，因此该算法实质上属于线性递归，其运行时间应线性正比于递归深度。进一步地，递归只可能发生于两个待合并堆的最右侧通路上，若待合并堆的规模分别为n和m，则其两条最右侧通路的长度分别不会超过$O(\log n)$和$O(\log m)$，因此合并算法总体运行时间应不超过：

$$O(\log n)+O(\log m)=O(\log n+\log m)=O(\log(\max(n,m)))$$

若将以上递归版本改写为迭代版本，还可以从常系数的意义上进一步提高效率。

3.6.基于合并的插入和删除

若将merge()操作当作一项更为基本的操作，则可以反过来实现优先级队列标准的插入和删除等操作。事实上，得益于merge()操作自身的高效率，如此实现的插入和删除操作，在时间效率方面不逊色与常规的实现方式，而其突出的简洁性也使得这一方式在实际中应用广泛。

3.6.1.delMax()

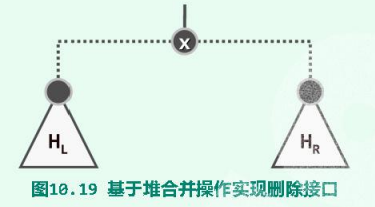
基于merge()操作实现delMax()算法，如图设堆顶x及其子堆$H_L$和$H_R$。在摘除x之后，$H_L$和$H_R$即可被视作为两个彼此独立的待合并的堆，只要通过merge()操作将它们合并其来，则效果完全等同于一次常规的delMax()删除操作。算法的时间复杂度依然不超过$O(\log n)$。

template <typename T> T PQ_LeftHeap<T>::delMax() {
   BinNodePosi(T) lHeap = _root->lc; if (lHeap) lHeap->parent = NULL; //左子堆
   BinNodePosi(T) rHeap = _root->rc; if (rHeap) rHeap->parent = NULL; //右子堆
   T e = _root->data; delete _root; _size--; //删除根节点
   _root = merge ( lHeap, rHeap ); //合并原左、右子堆
   if( _root ) _root->parent = NULL;  //若堆非空，还需相应设置父子连接
   return e; //返回原根节点的数据项
}

3.6.1.insert()

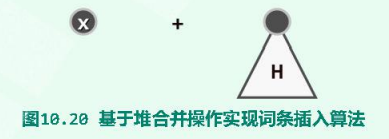
基于merge()操作实现insert()算法，假设拟将词条x插入堆H中。实际上，只要将x也视作（仅含单个节点的）堆，则通过调用merge()操作将该堆与堆H合并之后，其效果即完全等同完成了一次词条插入操作，时间复杂度依然不超过$O(\log n)$。

template <typename T> void PQ_LeftHeap<T>::insert ( T e ) {
   BinNodePosi(T) v = new BinNode<T> (e);  //为e创建一个二叉树节点
   _root = merge( _root, v);  //通过合并完成新节点的插入
   _root->parent = NULL;  //既然此时堆非空，还需相应设置父子连接
   //_root = merge( _root, new BinNode<T>( e, NULL ) ); //将e封装为左式堆，与当前左式堆合并
   _size++; //更新规模
}