0%

单目视觉里程计

发表于 更新于 本文字数： 15k
整理了一下这学期机器视觉课程的大作业。视觉里程计(Visual Odometry，VO)是一种利用连续的图像序列来估计相机或机器人移动距离的方法，要求基于OpenCV初步实现一个简单的视觉里程计，我主要参考了高翔的《视觉slam十四讲》来完成。

视觉里程计(Visual Odometry，VO)是一种利用连续的图像序列来估计相机或机器人移动距离的方法，也被称为Visual SLAM问题的前端，是移动机器人定位导航领域中的关键技术之一。作业要求基于OpenCV初步实现一个简单的视觉里程计，我主要参考了高翔的《视觉slam十四讲》来完成，并将项目上传到Github，地址为https://github.com/nekomoon404/slam-VO。下面整理了这次大作业的报告文档。

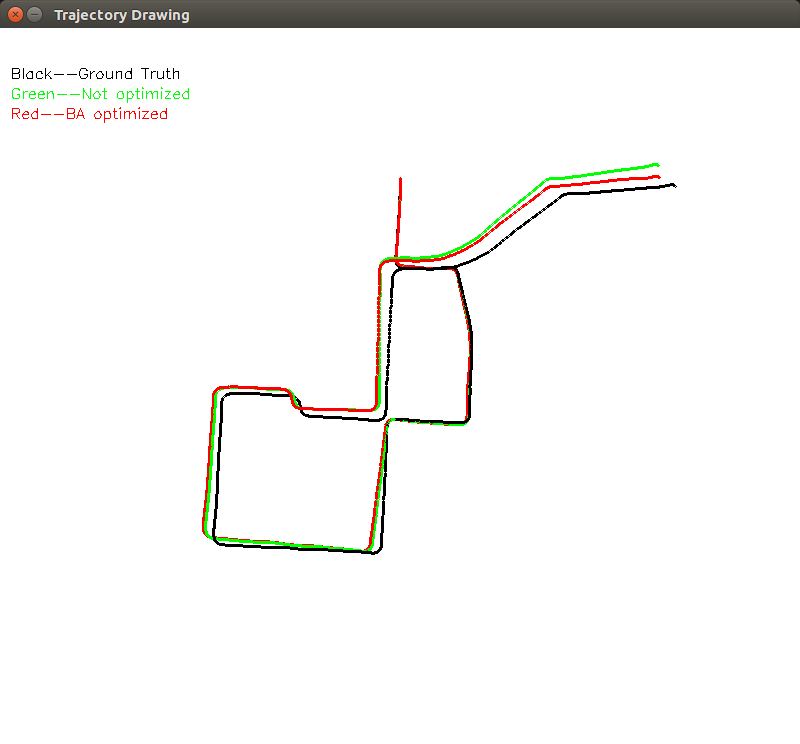
视觉里程效果截图

程序使用方法

运行环境：Ubuntu16.04+OpenCV3.4.0

安装程序所需的依赖库：线性代数库Eigen3，基于图优化的库g2o。

使用的数据集：KITTI数据集 灰度序列 /00/image_0 中的前2000帧图片

运行前更改slam-VO.h文件中第137行对应的路径：

1
ifstream myfile ("/home/neko/slam-VO/poses/00.txt");

更改slam-VO.cpp文件中第23到25行，以及第99行对应的路径：

1
2
3
4
5
sprintf(filename1, "/home/neko/slam-VO/00/image_0/%06d.png", 0);
sprintf(filename2, "/home/neko/slam-VO/00/image_0/%06d.png", 1);
string pose_path =  "/home/neko/slam-VO/poses/00.txt";

sprintf(filename, "/home/neko/slam-VO/00/image_0/%06d.png", numFrame);

进入/build文件夹，在终端依次执行来运行程序：

1
2
3
cmake ..
make
./slam-VO

算法详细介绍

程序的整体流程如下：

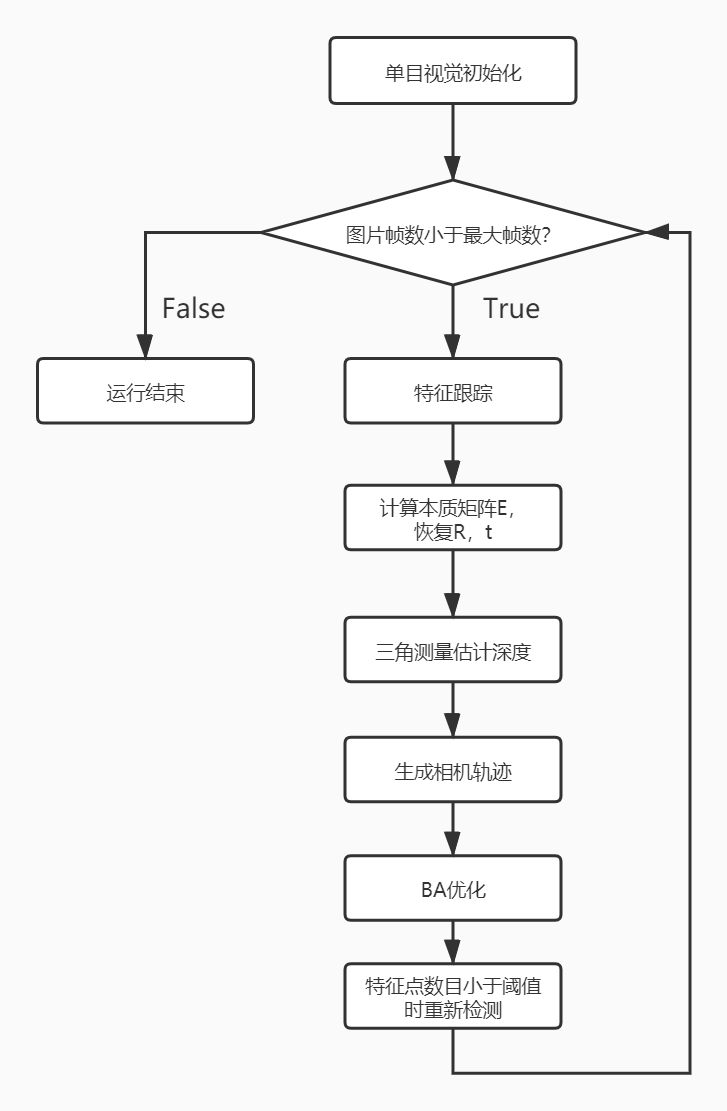
单目视觉初始化：

  1. 读取第一、二帧图片，并提取第一帧图片的特征点；
  2. 通过光流跟踪法得到第二帧图片的特征点，删除跟踪失败的点；
  3. 计算本质矩阵，并恢复运动，并以该转换矩阵作为初始值。

主循环：

连续读取图片，当读取图片帧数小于设定的最大帧数MAX_FRAME时：

  1. 光流跟踪前一帧图片特征点，得到当前帧特征点，并删除跟踪失败的点;
  2. 计算本质矩阵，并恢复旋转运动$\pmb{R}$和平移运动$\pmb{t}$；
  3. 根据匹配到的两帧特征点，进行三角测量，计算两帧图片之间的距离尺度scale;
  4. 由前一帧图片的位置、当前图片旋转、平移矩阵、距离尺度，计算得到当前图片的位置，生成相机轨迹；
  5. 进行BA优化；
  6. 保存优化后的平移运动结果，画出轨迹；
  7. 判断跟踪后的特征点数目是否大于设定阈值MIN_NUM_FEAT，若小于则重新检测

1.图片提取

根据网上的教程资料配置了Ubuntu16.04+OpenCV3.4.0的环境，具体步骤为：

  1. 下载OpenCV3.4.0 sources版本，解压

  2. 安装opencv的依赖库和cmake包，通过sudo apt-get install *命令进行安装

  3. 进入解压完的opencv文件夹，创建编译文件夹，mkdir build，依次执行cd build， cmake ..，make，make install。

  4. 配置OpenCV的编译环境，将OpenCV的库添加到路径，从而可以让系统找到，sudo gedit /etc/ld.so.conf.d/opencv.conf，在打开的文本中写入/usr/local/lib，执行sudo ldconfig

  5. 配置bash，执行sudo gedit /etc/bash.bashrc，在文本最末尾添加：

    1
    2
    PKG_CONFIG_PATH=$PKG_CONFIG_PATH:/usr/local/lib/pkgconfig
    export PKG_CONFIG_PATH

    保存，执行source /etc/bash.bashrc，使得配置生效：更新sudo updatedb

程序中使用sprintf()函数读入指定路径下的图片序列，用imread()函数读取当前图片，用imshow()函数显示当前图片。

1
2
3
4
5
sprintf(filename, /home/neko/slam-VO/00/image_0/%06d.png, numFrame);
cout << "Current frame number:"<<numFrame << endl;
currImage = imread(filename);

imshow( "CAMERA IMAGE", currImage);

2.提取特征点

视觉里程计的核心问题是如何根据图形估计相机运动，比较方便的做法是：首先从图像中选取比较有代表性的点，这些点在相机视角发生少量变化后会保持不变，于是能在各个图像中找到相同的点。然后在这些点的基础上讨论，讨论相机位姿估计问题，以及这些点的定位问题，这些点被称为图像特征。

在本次作业中我们提取FAST关键点，FAST 是一种角点，主要检测局部像素灰度变化明显的地方，以速度快著称。它的思想是：如果一个像素与它邻域的像素差别较大（过亮或过暗）, 那它更可能是角点。它的检测过程如下：

  1. 在图像中选取像素，假设它的亮度为$I_p$。
  2. 设置一个阈值$T$ (比如$I_p$的20%)。
  3. 以像素$p$为中心, 选取半径为3的圆上的16个像素点。
  4. 假如选取的圆上，有连续的$N$个点的亮度大于$I_p+T$ 或小于$I_p-T$，那么像素$p$可以被认为是特征点。
  5. 循环以上四步，对每一个像素执行相同的操作。

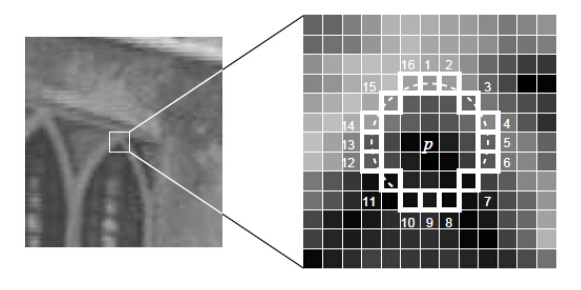
​ 图2-1 FAST特征点

OpenCV中默认采用Fast-9-16，即在周围取16个像素点，若超过连续9个点与中心点差值大于阈值即成为候选角点。为了更高效，可以进行预处理，检测圆周上第1.5.9.13个像素，当其中有三个及以上的符合阈值，才可以入围，若不符合，便可以直接排除。同时需要搜索局部极大值，抑制非极大值元素来避免角点集中的问题。

程序中通过featureDetection()函数来实现：

1
2
3
4
5
6
7
void featureDetection(Mat img_1, vector<Point2f>& points1)	{   
  vector<KeyPoint> kps;
  int fast_threshold = 10;
  Ptr<FastFeatureDetector> detector=FastFeatureDetector::create();
  detector->detect(img_1,kps);
  KeyPoint::convert(kps, points1, vector<int>());
}

3.特征跟踪与估计相机运动

3.1.光流法特征跟踪

使用光流（Optical Flow）来跟踪特征点的运动。这样可以回避计算和匹配描述子带来的时间。光流是一种描述像素随着时间，在图像之间运动的方法。随着时间的经过，同一个像素会在图像中运动。计算部分像素运动的称为稀疏光流，计算所有像素的称为稠密光流。稀疏光流以 Lucas-Kanade 光流为代表，并可以在 SLAM 中用于跟踪特征点位置。

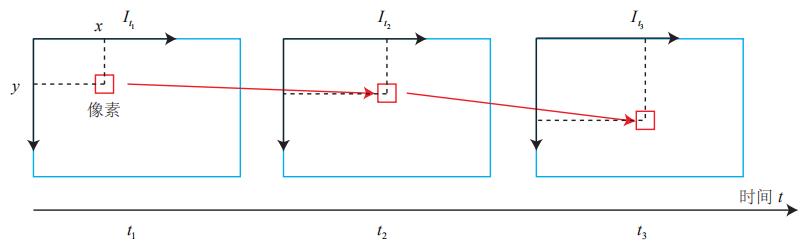
​ 图3-1 LK光流法示意图

在LK光流中，来自相机的图像是随时间变化的。图像可以看作时间的函数$I(t)$。那么，一个在$t$时刻，位于$(x,y)$处的像素，它的灰度可以写成$I(x,y,t)$。这种方式把图像看成了关于位置与时间的函数，它的值域就是图像中像素的灰度。

引入灰度不变假设：同一个空间点的像素灰度值，在各个图像中是固定不变的。对于t时刻位于$(x,y)$处的像素，设$t+dt$时刻，它运动到$(x + dx, y + dy)$处。由于灰度不变,有：

通过对左边进行泰勒展开，保留一阶项，两边同时除$dt$，并写成矩阵形式：

引入额外的约束来计算$u, \,\,v$，假设某一个窗口内的像素具有相同的运动，如一个大小为$w \times w$的窗口，它含有$w^2$数量的像素，因此共有$w^2$个方程：

这是一个关于$u,\,\, v$的超定线性方程，可以使用最小二乘法求解，这样就得到了像素在图像间的运动速度$u,\,\, v$。

如果相机运动较快，两张图像差异较明显，那么单层图像光流法容易达到一个局部极小值，这种情况可以通过引入图像金字塔来改善。图像金字塔是指对同一个图像进行缩放，得到不同分辨率下的图像。以原始的金字塔作为金字塔底层，每往上一层，就对下层图像进行一定倍率的缩放，就得到一个金字塔。然后在计算光流时，先从顶层的图像开始计算，然后把上一层的追踪结果，作为下一层光流的初始值。OpenCV中的calcOpticalFlowPyrLK()函数正是基于这一原理实现多层光流函数。

在程序中通过featureTracking()函数来实现特征跟踪：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void featureTracking(Mat img_1, Mat img_2, vector<Point2f>& points1, vector<Point2f>& points2, vector<uchar>& status)	
{ 
    vector<float>err;																		   
    calcOpticalFlowPyrLK(img_1, img_2, points1, points2, status, err);  //调用光流法跟踪特征点
    int indexCorrection = 0;
    for( int i=0; i<status.size(); i++)   //删除跟踪失败的点
    {  
        Point2f pt = points2.at(i- indexCorrection);
     	if ((status.at(i) == 0)||(pt.x<0)||(pt.y<0))	
        {
     		  if((pt.x<0)||(pt.y<0))
               {
     		  	status.at(i) = 0;
     		  }
     		  points1.erase (points1.begin() + (i - indexCorrection));
     		  points2.erase (points2.begin() + (i - indexCorrection));
     		  indexCorrection++;
     	}
     }
}

3.2.对极几何估计相机运动

接下来根据匹配的点对估计相机的运动。当相机为单目时，只知道2D的像素坐标，因而问题是根据两组2D点估计运动，可以用对极几何来解决。

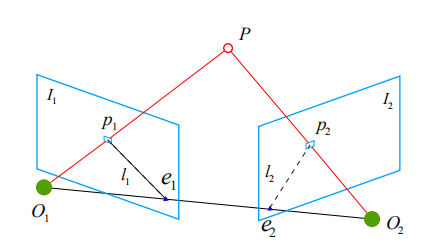
​ 图3-2 对极几何约束

如下图所示，我们希望求取两帧图像$I_1$，$I_2$之间的运动，设第一帧到第二帧的运动为$R$，$t$。两个相机中心分别为$O_1$，$O_2$现在，考虑$I_1$ 中有一个特征点$p_1$，它在$I_2$中对应着特征点$p_2$。根据针孔相机模型，可得两个像素点的$p_1$，$p_2$的像素位置：

其中$K$为相机内参，$R$，$t$为两个坐标系的相机运动。使用齐次坐标表示像素点，例如$s_1p_1$和$s_2p_2$成投影关系，它们在齐次坐标下的意义是相等的，称为尺度意义下相等。经推导得到对极约束的表达式：

把中间部分记作两个矩阵：基础矩阵（Fundamental Matrix）$F$ 和本质矩阵（Essential Matrix）$E$，可以进一步简化对极约束：

对极约束简洁地给出了两个匹配点的空间位置关系，相机位姿估计问题变为以下两步：

  1. 根据配对点的像素位置，求出$E$ 或者$F$；
  2. 根据$E$或者$F$，求出$R$，$t$。

在程序中我们使用本质矩阵$E$求解，然后通过本质矩阵获取摄像机的相对旋转和平移量：

1
2
3
//计算本质矩阵并恢复R,t
E = findEssentialMat(prevFeatures, currFeatures, focal_length, principal_point, RANSAC, 0.999, 1.0, mask);
recoverPose(E, prevFeatures,currFeatures,  R, t, focal_length, principal_point, mask);

3.3.三角测量

在单目SLAM 中，仅通过单张图像无法获得像素的深度信息，我们需要通过三角测量（Triangulation）（或三角化）的方法来估计地图点的深度。三角测量是指，通过在两处观察同一个点的夹角，确定该点的距离。在SLAM 中主要用三角化来估计像素点的距离。

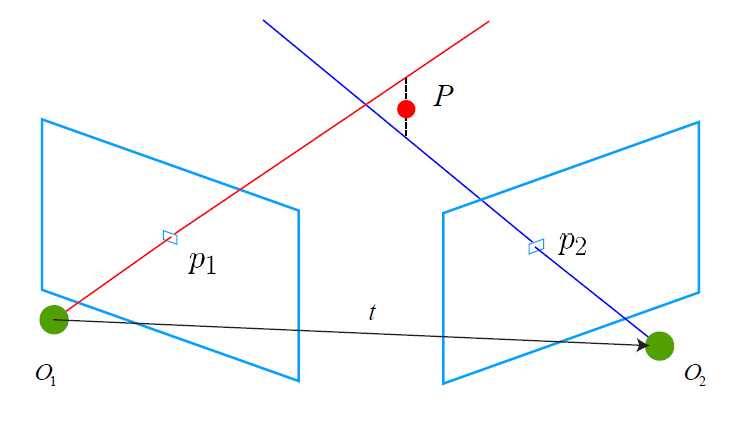
​ 图3-2 通过三角测量的方法获得地图点的深度

论上直线$O_1p_1$ 与 $O_2p_2$在场景中会相交于一点$P$，该点即是两个特征点所对应的地图点在三维场景中的位置。然而由于噪声的影响，这两条直线往往无法相交。因此，可以通过最二小乘去求解。设$x_1$，$x_2$为两个特征点的归一化坐标，那么它们满足：

如果要算$s_1$，那么先对上式两侧左乘一个$x_2^\land$，得：

该式左侧为零，右侧可以看成是$s_2$的一个方程，根据它可求出$s_2$，进而能求出$s_1$。这样就得到了两帧下的深度，确定了它们的空间坐标。由于噪声的存在，估得的$R,t$不一定精确使上式为零，所以常用最小二乘法求解。

在程序中通过triangulation()函数实现三角测量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
void triangulation ( 
    const vector< Point2f>& points_1, 
    const vector< Point2f>& points_2, 
    const Mat& R, const Mat& t, 
    vector< Point3f >& points)
{
   Mat T1 = (Mat_<float> (3,4) <<
        1,0,0,0,
        0,1,0,0,
        0,0,1,0);
    Mat T2 = (Mat_<float> (3,4) <<
        R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2), t.at<double>(0,0),
        R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2), t.at<double>(1,0),
        R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2), t.at<double>(2,0)
    );
    Mat K = ( Mat_<double> ( 3,3 ) << 718.856, 0, 607.1928, 0, 718.856, 185.2157, 0, 0, 1 );
    vector<Point2f> pts_1, pts_2;
    for ( int idex=0;idex<points_1.size();idex++ )
    {
        // 将像素坐标转换至相机坐标
        pts_1.push_back ( pixel2cam( points_1[idex], K) );
        pts_2.push_back ( pixel2cam( points_2[idex], K) );
    }

    Mat pts_4d;
    cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
    
    // 转换成非齐次坐标
    for ( int i=0; i<pts_4d.cols; i++ )
    {
        Mat x = pts_4d.col(i);
        x /= x.at<float>(3,0); // 归一化
        Point3f p (
            x.at<float>(0,0), 
            x.at<float>(1,0), 
            x.at<float>(2,0) 
        );
        points.push_back( p );
    }
}

4.生成相机轨迹与Ground Truth比较

Ground Truth轨迹绘制，通过读取00.txt中的数据绘制，slam-VO.h文件中定义了get_Pose()函数，slam-VO.cpp中函数调用程序如下：

1
2
3
vector<vector<float>> poses = get_Pose(pose_path);
Point2f trace1 = Point2f(int(poses[numFrame][3]) + 400, int(poses[numFrame][11]) + 150); //绘制Ground Truth      
circle(trace, trace1, 1, Scalar(0,0,0), 1);

初步未优化得到的相机运动轨迹绘制，在三角测量得到特征点三维信息后，通过判断两帧间是否有一定程度的位移决定该次三角测量精度是否准确，若可以，则绘制当前位置点，程序如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//三角测量
triangulation (prevFeatures,currFeatures,R,t,points);
cout<<"id<points.size():"<<points.size()<<endl;        	
for ( int id=0; id<points.size(); id++ ){
	 points1.push_back(prevFeatures[id]);
     points2.push_back(currFeatures[id]);
} 
        
scale = getAbsoluteScale(numFrame, 0, t.at<double>(2));//平移的距离     
if ((scale>0.1)&&(-t.at<double>(2) > -t.at<double>(0)) && (-t.at<double>(2) > -t.at<double>(1))){    //确保有一定程度的平移而不是纯旋转以保证三角测量的精度 
	 t_f = t_f + scale*(R_f*(-t));
     R_f = R.inv()*R_f;			
     pre_t=t.clone();
     int x = int(t_f.at<double>(0)) + 400;
     int y = int(t_f.at<double>(2)) + 150; 
     Point2f trace2 = Point2f(x,y) ;     
     circle(trace, trace2 ,1, Scalar(0,255,0), 1);//绘制初步估计的轨迹
}
else{
     cout << "scale below 0.1, or incorrect translation" << endl;
}

5.Bundle Adjustment优化

PnP用于求解3D到2D运动的投影位置方法。可以通过线性方法先求解相机位姿再求解空间投影点，但存在的问题是线性解法鲁棒性不太好，并且需要建立线性方程求代数解较为困难。因此，当运动比较连续时，一般选择非线性优化方法来进行迭代求解最优解，通常采用基于最小二乘问题的Bundle Adjustment(BA, 捆集调整)方法。针对本文采用的单目相机数据集，必须先对其进行初始化，再使用BA算法。

非线性优化将相机位姿、空间特征点等多个参数看作优化变量。如上图所示，根据之前的特征匹配，已知$p_1$、$p_2$为同一空间点的两个投影点，利用最小化重投影误差对相机位姿进行优化，使计算得到的$p_2’$与实际$p_2$不断接近，直到达到精度范围或最大迭代次数。设相机位姿变换为$R$，$t$，对应李代数为$\xi$。相机内参矩阵为$K$。任一三维空间点P的坐标$ \pmb{P}_i=[X_i,Y_i,Z_i]^T$。对应的投影像素坐标为$\pmb{u}_i=[u_i,v_i]^T$。则像素点与空间点存在如下关系：

即：

因此，以相机位姿李代数$\xi$、特征点空间位置等为优化变量，以重投影误差为目标函数，计算将像素坐标观测值与按相机位姿计算得到的像素坐标计算值之间的误差，构建最小二乘问题，利用Gauss-Newton法或Levenburg-Marquadt优化算法寻找最优相机位姿和特征点空间坐标。优化模型如下所示：

在利用优化算法进行迭代的时候，最重要的是计算每次迭代的下降梯度方向，对目标函数误差求导可得：

其中，$J$为$2 \times 6$的雅各比矩阵。通过扰动模型求解李代数导数，计算过程如下：由上文已知像素点与空间点的关系，设$\pmb{P}’$为空间点$\pmb{P}$经相机位姿变换后的空间坐标，即$\pmb{P}’=(\exp(\pmb{\xi}^\land)\pmb{P})_{1:3}=[X’,Y’,Z’]^T$。将相机内参$K$展开得：

消元可得：

将相机位姿李代数左乘扰动量$\delta \pmb{\xi}$，再通过误差变化对扰动量的求导可得：

误差变化$e$对于$\pmb{P}’$的求导可以根据之前消元得到的$u$、$v$表达式得到：

$\pmb{P}’$对扰动量$\delta \pmb{\xi}$求导为：

于是最终得到相机位姿导数的雅各比矩阵：

同理，对于特征点空间位置的优化，还需要将误差$e$对空间点$\pmb{P}$进行求导，可以得到如下计算模型：

基于以上推导，采用g2o库实现相机位姿图优化，部分代码如下图所示。图优化时以下一个相机位姿和所有特征点空间坐标为节点，以下一个相机中的投影坐标为边。以RANSAC PnP结果为初值，调用g2o进行优化。

slam-VO.h文件中定义 Bundle Adjustment()函数程序如下：函数输入前一帧的三维信息和后一帧的两维信息，以及相机内参矩阵，则可得到优化后的相机变化位姿矩阵。函数定义中，首先初始化g2o，定义优化求解器，定义图优化的边和节点，定义误差函数等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
void bundleAdjustment (
    vector< Point3f > points_3d,
    vector< Point2f > points_2d,
    Mat K,
    Mat R, Mat t,
    Mat& RR, Mat& tt )
{
    // 初始化g2o
    typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block; 
    // pose 维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
    Block* solver_ptr  = new Block (linearSolver);    // 矩阵块求解器
    
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg (solver_ptr);
    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm ( solver );

    // vertex
    g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
    Eigen::Matrix3d R_mat;
    R_mat <<
               R.at<double> ( 0,0 ), R.at<double> ( 0,1 ), R.at<double> ( 0,2 ),
               R.at<double> ( 1,0 ), R.at<double> ( 1,1 ), R.at<double> ( 1,2 ),
               R.at<double> ( 2,0 ), R.at<double> ( 2,1 ), R.at<double> ( 2,2 );
    pose->setId ( 0 );
    pose->setEstimate ( g2o::SE3Quat (R_mat,Eigen::Vector3d ( t.at<double> ( 0,0 ), t.at<double> ( 1,0 ), t.at<double> ( 2,0 ) ) ) );
    optimizer.addVertex ( pose );

    int index = 1;
    for ( const Point3f p:points_3d )   // landmarks
    {
        g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
        point->setId ( index++ );
        point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
        point->setMarginalized ( true ); 
        optimizer.addVertex ( point );
    }

    // parameter: camera intrinsics
    g2o::CameraParameters* camera = new g2o::CameraParameters ( K.at<double> ( 0,0 ), Eigen::Vector2d ( K.at<double> ( 0,2 ), K.at<double> ( 1,2 ) ), 0 );
    camera->setId ( 0 );
    optimizer.addParameter ( camera );

    // edges
    index = 1;
    for ( const Point2f p:points_2d )
    {
        g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
        edge->setId ( index );
        edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
        edge->setVertex ( 1, pose );
        edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
        edge->setParameterId ( 0,0 );
        edge->setInformation ( Eigen::Matrix2d::Identity() );
	edge->setRobustKernel( new g2o::RobustKernelHuber() );
        optimizer.addEdge ( edge );
        index++;
    }

    optimizer.setVerbose ( false );
    optimizer.initializeOptimization();
    optimizer.optimize ( 5);
    
    Eigen::Isometry3d T = Eigen::Isometry3d ( pose->estimate() );
    //RR、t为优化后的R和t
    RR=(Mat_<double>(3,3)<<
    T(0,0),T(0,1),T(0,2),
    T(1,0),T(1,1),T(1,2),
    T(2,0),T(2,1),T(2,2));

    tt=(Mat_<double>(3,1)<<
    T(0,3),T(1,3),T(2,3));
}

slam-VO.cpp文件中调用该函数程序如下：输入前后两帧的三维特征信息、相机内参、相机变换位姿，可以返回 优化后的位资矩阵。同样，需要判断两帧间平移是否到达一定程度，否则需要进行尺度修正。然后将每次循环得到的轨迹进行实时绘制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//BA优化
bundleAdjustment ( points,points2, K,R,t, RR,tt );
if ((scale>0.1)&&(-tt.at<double>(2) > -tt.at<double>(0)) && (-tt.at<double>(2) > -tt.at<double>(1)))
{		
	if(abs(tt.at<double>(2)-t.at<double>(2))<0.05)
    {
		 t_E = t_E + scale*(R_E*(-tt));
      	 R_E = RR.inv()*R_E;
         pre_t=tt.clone();								
	}
	else
    {	
         cout<<"优化失败"<<endl;                        	
		 t_E = t_E + scale*(R_E*(-t));
         R_E = R.inv()*R_E;			
         pre_t=t.clone();						
	}								     		       	
}
else
{
     cout << "scale below 0.1, or incorrect translation" << endl;
}
Point2f trace3 = Point2f(int(t_E.at<double>(0)) + 400, int(t_E.at<double>(2)) + 150);
circle(trace, trace3, 1, Scalar(0,0,255), 1);//绘制BA优化后的轨迹

得到的BA优化轨迹如图中红色轨迹所示，右上角可以看出，累积误差较大的时候，BA优化的轨迹展示出了更好的性能。由于这里只考虑相邻两帧之间的优化，因此随着累积误差的增大，对极约束估计以及BA优化得到的轨迹效果都越来越差，需要通过局部地图以及后端的回环检测等方法来优化。