这周开始学李宏毅老师的Machine Learning 2020的课程了，从第一节课的课程概述来看，这门课除了会介绍传统的Machine Learning算法外，还会介绍很多Deep Learning的内容，时长也是非常感人(ㄒoㄒ)，希望自己能坚持学下去吧。

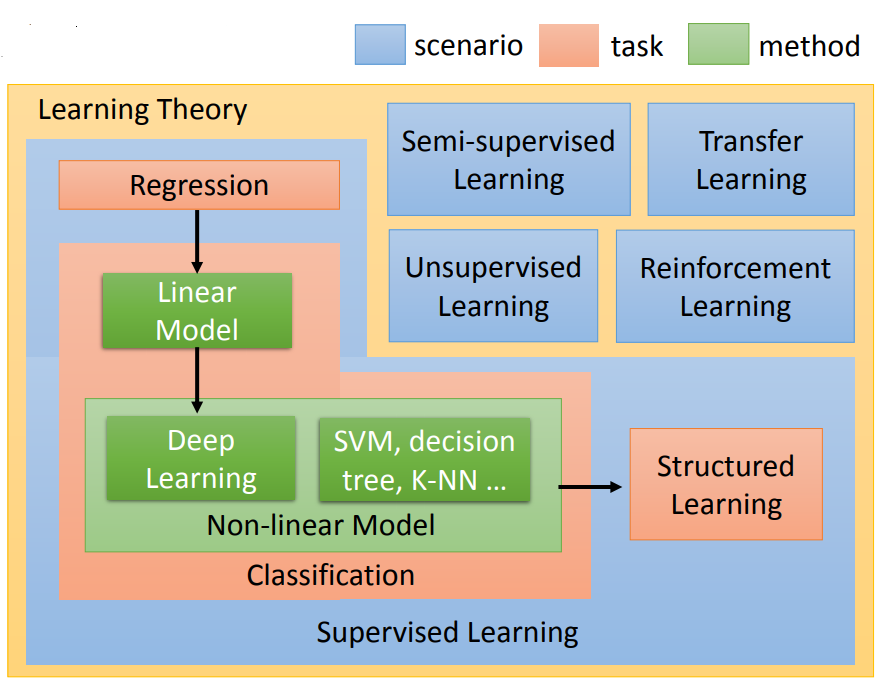
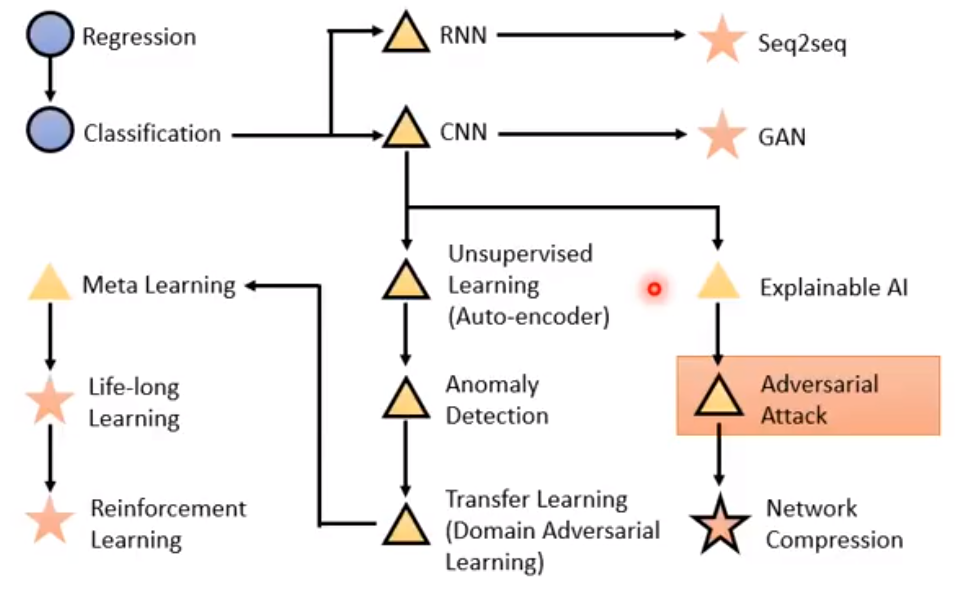
前面几节课（p3-p7）分别讲了回归 Regression，误差来源 Where does the error come from，梯度下降 Gradient Descent，老师用的预测宝可梦pokemon的CP值的例子还是蛮有趣的hhh。这部分的理论内容自己是比较熟悉，也有之前做的纸质笔记，在这里就不详细展开了，这里主要写一下使用Gradient Descent的Tips，以及其背后的Theory。

1. Gradient Descent Tips

1.1.Tip 1: Tuning your learning rates

gradient descent过程中，影响结果的一个很关键的因素就是learning rate的大小

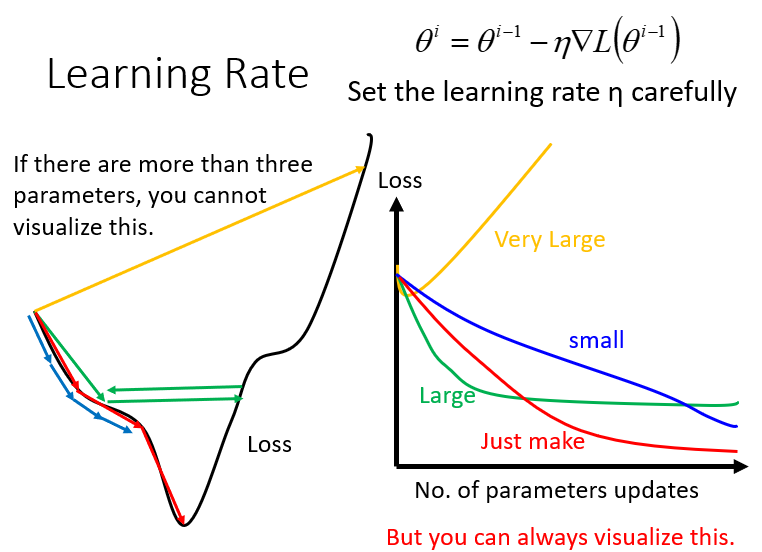
当参数有很多个的时候(>3)，其实我们很难做到将loss随每个参数的变化可视化出来(因为最多只能可视化出三维的图像，也就只能可视化三维参数)，但是我们可以把update的次数作为唯一的一个参数，将loss随着update的增加而变化的趋势给可视化出来(上图右半部分)

所以做gradient descent时可以把不同的learning rate下，loss随update次数的变化曲线给可视化出来，它可以提醒你该如何调整当前的learning rate的大小，直到出现稳定下降的曲线

Adaptive Learning rates

显然这样手动地去调整learning rates很麻烦，因此我们需要有一些自动调整learning rates的方法。最基本、最简单的大原则是：learning rate通常是随着参数的update越来越小的。可以这样理解：在起始点的时候，通常是离最低点是比较远的，这时候步伐就要跨大一点；而经过几次update以后，会比较靠近目标，这时候就应该减小learning rate，让它能够收敛在最低点的地方。如可以设置到了第t次update，$\eta^t=\eta/ \sqrt{t+1}$。

这种方法使所有参数以同样的方式同样的learning rate进行update，而最好的状况是每个参数都给他不同的learning rate去update

Adagrad

Adagrad就是将不同参数的learning rate分开考虑的一种算法(adagrad算法update到后面速度会越来越慢，当然这只是adaptive算法中最简单的一种)。

这里的$w$是function中的某个参数，$t$表示第$t$次update，$g^t$表示Loss对$w$的偏微分，而$\sigma^t$是之前所有Loss对$w$偏微分的均方根 root mean square这个值对每一个参数来说都是不一样的。

$\begin{equation} \begin{split} &Adagrad\\ &w^1=w^0-\frac{\eta^0}{\sigma^0}\cdot g^0 \ \ \ \sigma^0=\sqrt{(g^0)^2} \\ &w^2=w^1-\frac{\eta^1}{\sigma^1}\cdot g^1 \ \ \ \sigma^1=\sqrt{\frac{1}{2}[(g^0)^2+(g^1)^2]} \\ &w^3=w^2-\frac{\eta2}{\sigma^2}\cdot g^2 \ \ \ \sigma^2=\sqrt{\frac{1}{3}[(g^0)^2+(g^1)^2+(g^2)^2]} \\ &... \\ &w^{t+1}=w^t-\frac{\eta^t}{\sigma^t}\cdot g^t \ \ \ \sigma^t=\sqrt{\frac{1}{1+t}\sum\limits_{i=0}^{t}(g^i)^2} \end{split} \end{equation}$

由于$\eta^t$和$\sigma^t$中都有一个$\sqrt{\frac{1}{1+t}}$的因子，两者相消，即可得到Adagrad的最终表达式：

$w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum\limits_{i=0}^t(g^i)^2}}\cdot g^t$

对Adagrad中的contradiction的解释

Adagrad的表达式$w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum\limits_{i=0}^t(g^i)^2}}\cdot g^t$里面有一件很矛盾的事情：我们在做gradient descent的时候，希望的是当梯度值即微分值$g^t$越大的时候(此时斜率越大，还没有接近最低点)更新的步伐要更大一些，但是Adagrad的表达式中，分母表示梯度越大步伐越大，分子却表示梯度越大步伐越小，两者似乎相互矛盾。

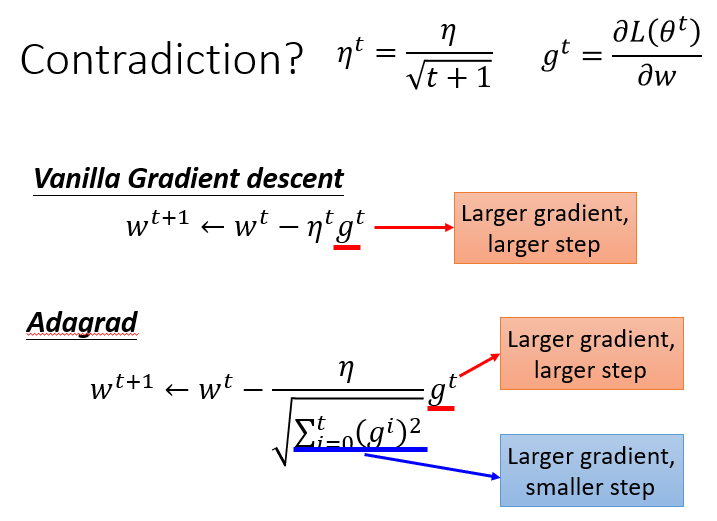
在一些paper里是这样解释的：Adagrad要考虑的是，这个gradient有多surprise，即反差有多大，假设t=4的时候$g^4$与前面的gradient反差特别大，那么$g^t$与$\sqrt{\frac{1}{t+1}\sum\limits_{i=0}^t(g^i)^2}$之间的大小反差就会比较大，它们的商就会把这一反差效果体现出来。

而且需要注意的是：gradient越大，离最低点越远，这个有点直观的想法在有多个参数的情况下是不一定成立的。如下图所示，$w_1$和$w_2$分别是loss function的两个参数，loss的值投影到该平面中以颜色深度表示大小，分别在$w_2$和$w_1$处垂直切一刀(这样就只有另一个参数的gradient会变化)，对应的情况为右边的两条曲线，可以看出，比起a点，c点距离最低点更近，但是它的gradient却越大。

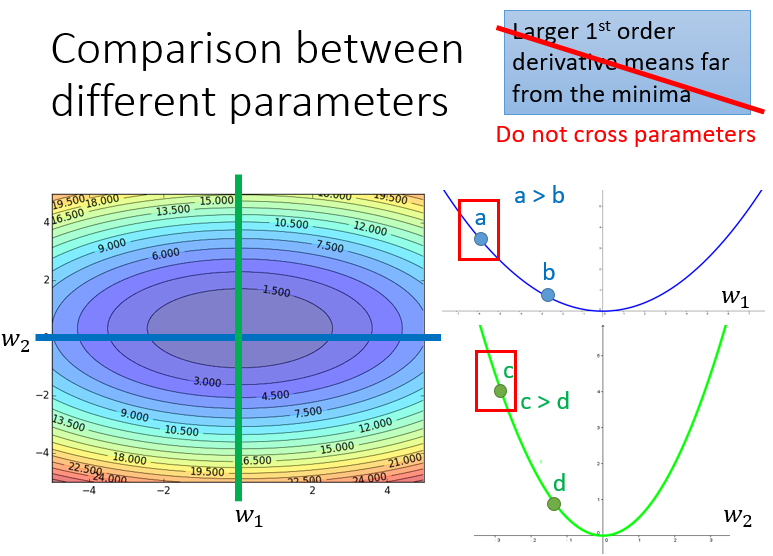
考虑一个简单的情况，对于一个二次函数$y=ax^2+bx+c$来说，最小值点的$x=-\frac{b}{2a}$，而对于任意一点$x_0$，它迈出最好的步伐长度是$|x_0+\frac{b}{2a}|=|\frac{2ax_0+b}{2a}|$(这样就一步迈到最小值点了)，联系该函数的一阶和二阶导数$y’=2ax+b$、$y’’=2a$，可以发现the best step 就是 $|\frac{y’}{y’’}|$，即|一阶导数|/|二阶导数|，可见best step不仅跟一阶导数(gradient)有关，还跟二阶导数有关，用这个best step可以来反映Loss Function上一点到最低点的距离。

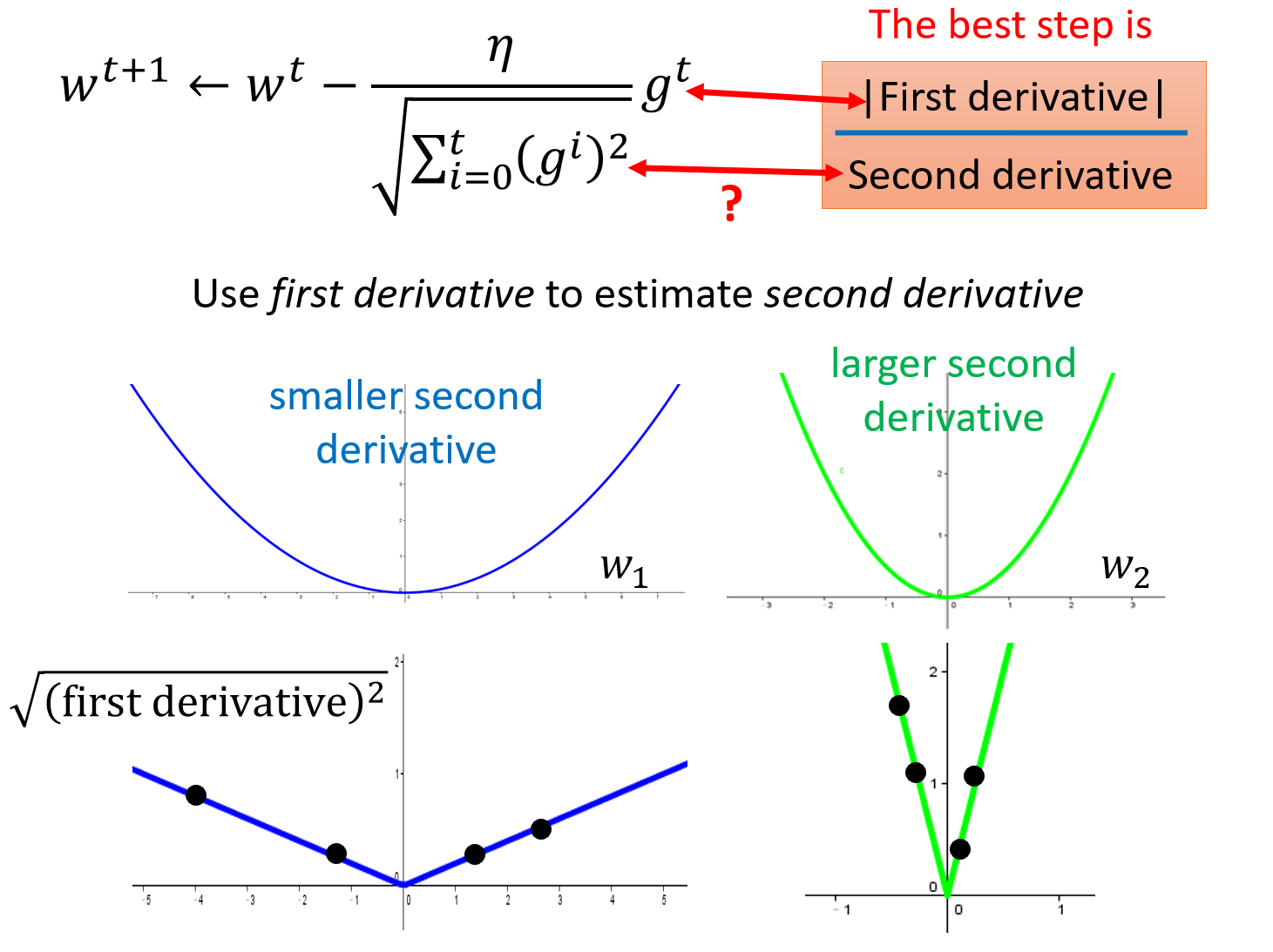
再来回顾Adagrad的表达式：

$w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum\limits_{i=0}^t(g^i)^2}}\cdot g^t$

其中，$g^t$是一次微分，而分母中的$\sqrt{\sum\limits_{i=0}^t(g^i)^2}$则反映了二次微分的大小。Adagrad中用root mean square of the previous derivatives of parameter w来近似二次微分的大小，避免引入额外的计算量。

1.2.Tip 2: Stochastic Gradient Descent

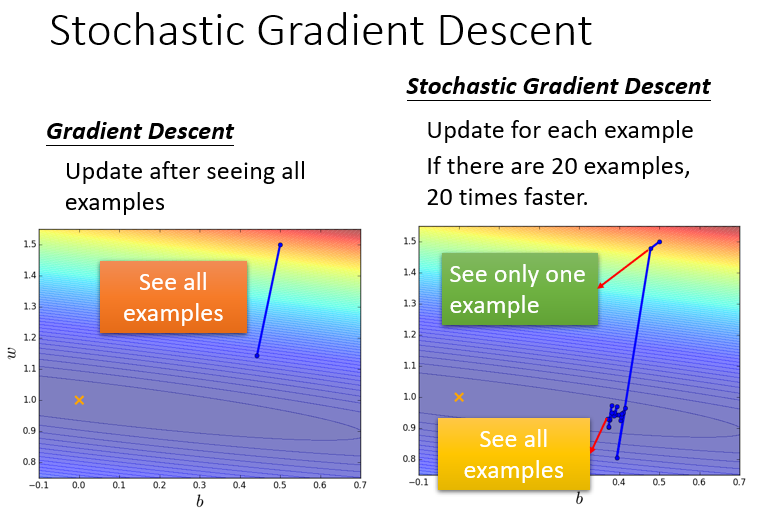
随机梯度下降 Stochastic Gradient Descent的方法可以让训练更快速，传统的gradient descent的思路是遍历所有的样本点之后再构建loss function，然后去update参数；而stochastic gradient descent的做法是，看到一个样本点就update一次，因此它的loss function不是所有样本点的error平方和，而是这个随机样本点的error平方。

Stochastic Gradient Descent与传统Gradient Descent的效果对比如下：

1.3.Tip 3: Feature Scaling

特征缩放Feature Scaling，当多个特征的尺度很不一样时，最好将这些不同feature的范围缩放成一样的。

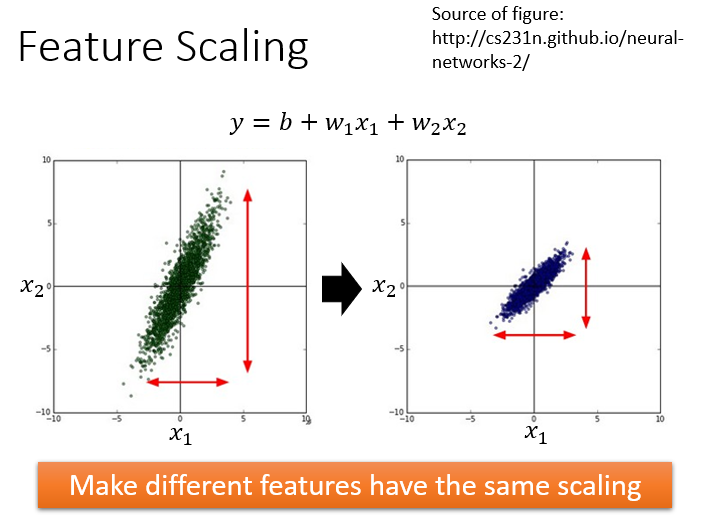
举个例子来解释为什么需要做feature scaling，$y=b+w_1x_1+w_2x_2$，假设$x_1$的值都是很小的，比如1,2…；$x_2$的值都是很大的，比如100,200…。此时去画出loss的error surface，如果对$w_1$和$w_2$都做一个同样的变动$\Delta w$，那么$w_1$的变化对$y$的影响是比较小的，而$w_2$的变化对$y$的影响是比较大的。

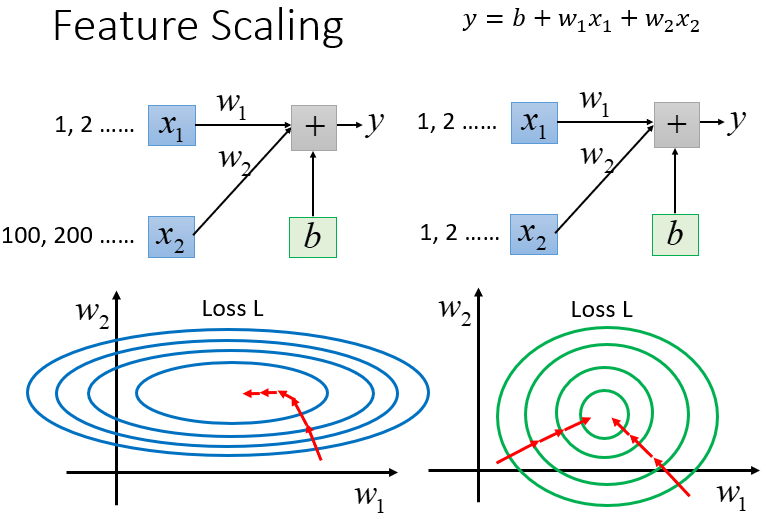
左边的error surface表示，w1对y的影响比较小，所以w1对loss是有比较小的偏微分的，因此在w1的方向上图像是比较平滑的；w2对y的影响比较大，所以w2对loss的影响比较大，因此在w2的方向上图像是比较sharp的。如果x1和x2的的scale是接近的，那么w1和w2对loss就会有差不多的影响力，loss的图像接近于圆形，那这样做对gradient descent有什么好处呢？

对Gradient Descent的帮助

之前我们做的demo已经表明了，对于这种长椭圆形的error surface，如果不使用Adagrad之类的方法，是很难搞定它的，因为在像w1和w2这样不同的参数方向上，会需要不同的learning rate，用相同的learning rate很难达到最低点。如果x1和x2有相同的scale的话，loss在参数w1、w2平面上的投影就是一个正圆形，update参数会比较容易。

而且gradient descent的每次update并不都是向着最低点走的，每次update的方向是顺着等高线的方向(梯度gradient下降的方向)，而不是径直走向最低点；但是当经过对input的scale使loss的投影是一个正圆的话，不管在这个区域的哪一个点，它都会向着圆心走。因此feature scaling对参数update的效率是有帮助的

如何做feature scaling

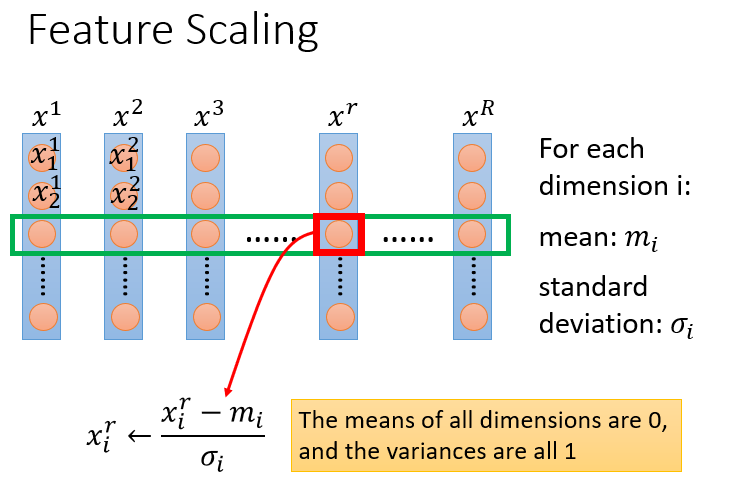
假设有R个example(上标i表示第i个样本点)，$x^1,x^2,x^3,…,x^r,…x^R$，每一个example，它里面都有一组feature(下标j表示该样本点的第j个特征)

对每一个feature (demension) i，都去算出它的平均值mean=$m_i$，以及标准差standard deviation=$\sigma_i$

对第r个example的第i个feature的值，减掉均值，除以标准差，即：

$x_i^r=\frac{x_i^r-m_i}{\sigma_i}$

2.Gradient Descent Theory

考虑当用梯度下降解决问题：

$\theta^*=\arg \underset{\theta}{\min} L(\theta)$

每次更新参数 $\theta$，都得到一个新的$ \theta$，它都使得损失函数更小。即：

$L(\theta^0)>L(\theta^1)>L(\theta^2)>\dots$

上述结论正确吗？其实是不正确的，我们并不能每次更新$\theta$，都能使损失函数更小。那么如何更新$\theta$才能使损失函数更小呢。

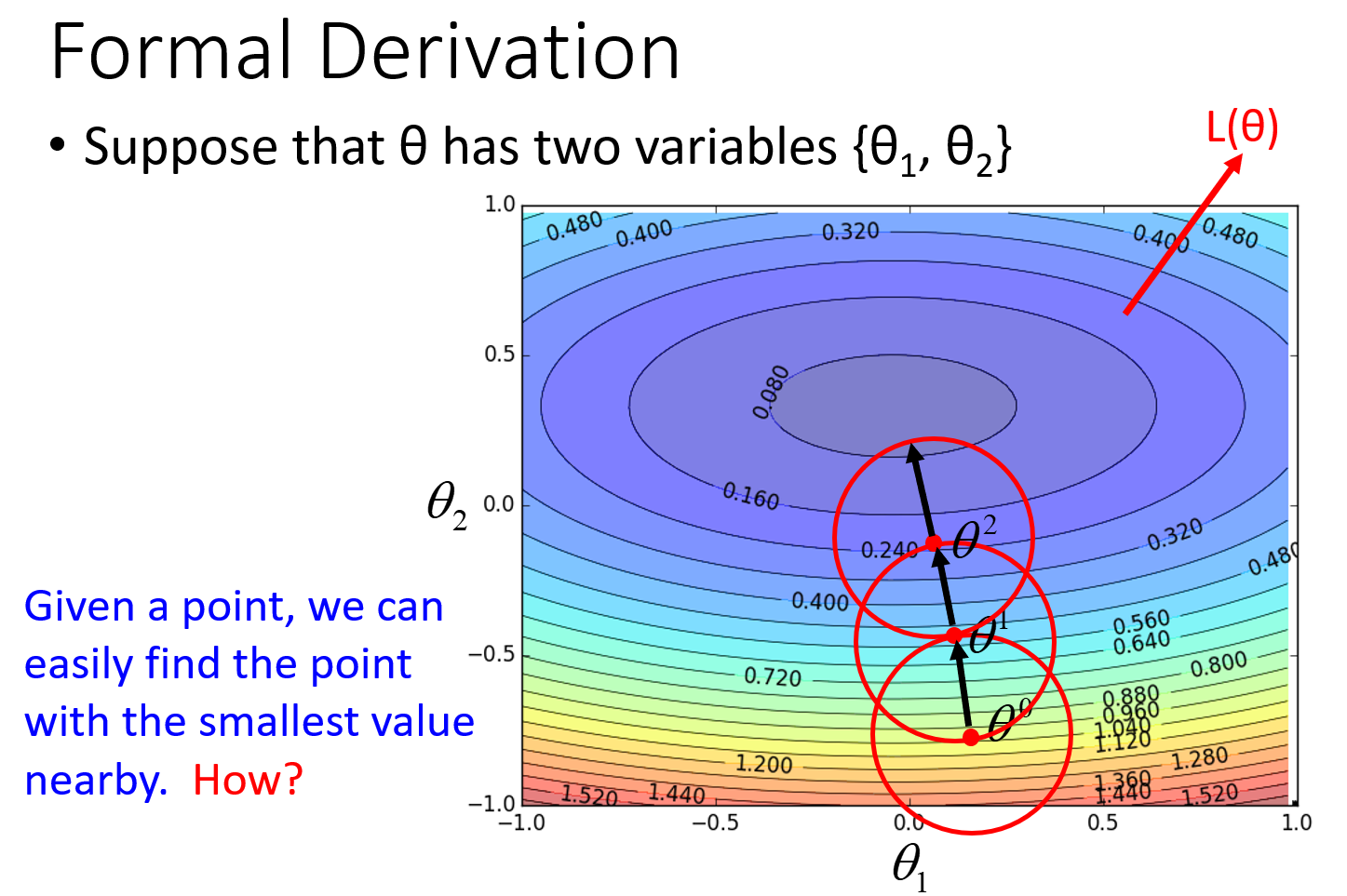
比如在$\theta^0$ 处，可以在一个小范围的圆圈内找到使损失函数最小的$\theta^1$，不断的这样去寻找。接着就考虑如何在这样一个小圆圈中寻找到$\theta^1$。这里就需要引入泰勒展开式（高数里都有讲啦）。

回到刚才的问题上，我们将点(a,b)附件的小圆内的损失函数在点(a,b)处展开：

$L(\theta)≈L(a,b)+\frac{\partial L(a,b)}{\partial \theta_1}(\theta_1-a)+\frac{\partial L(a,b)}{\partial \theta_2}(\theta_2-b)$

令

$s=L(a,b),\quad u=\frac{\partial L(a,b)}{\partial \theta_1},\quad v=\frac{\partial L(a,b)}{\partial \theta_2}$

则

$L(\theta)≈s + u\cdot (\theta_1-a)+v\cdot (\theta_2-b)$

设红色圆圈的半径为d，则有限制条件：

$(\theta_1-a)^2+(\theta_2-b)^2≤d^2$

求$L(\theta)_{min}$，这里有个小技巧，把$L(\theta)$转化为两个向量的乘积：

$u\cdot (\theta_1-a)+v\cdot (\theta_2-b)=(u,v)\cdot (\theta_1-a,\theta_2-b)=(u,v)\cdot (\Delta \theta_1,\Delta \theta_2)$

显然，当向量$(\theta_1-a,\theta_2-b)$与向量$(u,v)$反向，且刚好到达red circle的边缘时(用$\eta$去控制向量的长度)，$L(\theta)$最小。

于是$L(\theta)$局部最小值对应的参数为中心点减去gradient的加权：

$\begin{bmatrix} \Delta \theta_1 \\ \Delta \theta_2 \end{bmatrix}= -\eta \begin{bmatrix} u \\ v \end{bmatrix}=> \begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix}= \begin{bmatrix} a\\ b \end{bmatrix}-\eta \begin{bmatrix} u\\ v \end{bmatrix}= \begin{bmatrix} a\\ b \end{bmatrix}-\eta \begin{bmatrix} \frac{\partial L(a,b)}{\partial \theta_1}\\ \frac{\partial L(a,b)}{\partial \theta_2} \end{bmatrix}$

这就是gradient descent在数学上的推导，注意它的重要前提是，设定的红色圈圈的范围要足够小，这样泰勒展开给我们的近似才会精确，而$\eta$的值是与圆的半径成正比的，因此理论上learning rate要无穷小才能够保证每次gradient descent在update参数之后的loss会越来越小。于是当learning rate没有设置好，泰勒近似不成立，就有可能使gradient descent过程中的loss没有越来越小

当然泰勒展开可以使用二阶、三阶乃至更高阶的展开，但这样会使得运算量大大增加，反而降低了运行效率。

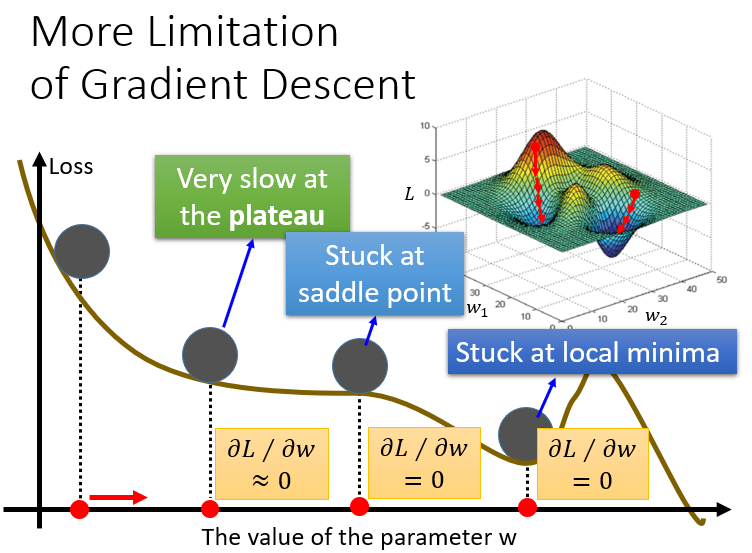
3.More Limitation of Gradient Descent

之前已经讨论过，gradient descent有一个问题是它会停在local minima的地方就停止update了。事实上还有一个问题是，微分值是0的地方并不是只有local minima，settle point （鞍点）的微分值也是0。以上都是理论上的探讨，到了实践的时候，其实当gradient的值接近于0的时候，我们就已经把它停下来了，但是微分值很小，不见得就是很接近local minima，也有可能是在一个鞍点上。还有个限制就是在”坡度“小的区域update得很慢。总结一下就是下面三点：

Very slow at the plateau
Stuck at saddle point
Stuck at local minima