1.Classification
这节课的例子是对宝可梦进行分类(老宝可梦训练大师了),宝可梦有18种属性,现在要解决的分类问题就是做一个宝可梦种类的分类器,我们要找一个function,这个function的input是某一只宝可梦,它的output就是这只宝可梦属于这18类别中的哪一个type。
对每一只宝可梦(比如皮卡丘),可以用7个feature的数值组成的vector来描述它。

把编号400以下的宝可梦当做training data,编号400以上的当做testing data。这里我们先只考虑二分类,只考虑水系Water和一般系Normal宝可梦。
1.1.Classification as Regression?
以binary classification为例,我们在Training时让输入为class 1的输出为1,输入为class 2的输出为-1;那么在testing的时候,regression的output是一个数值,它接近1则说明它是class 1,它接近-1则说明它是class 2。但Regression中对“好,坏”的定义并不适用于Classification。
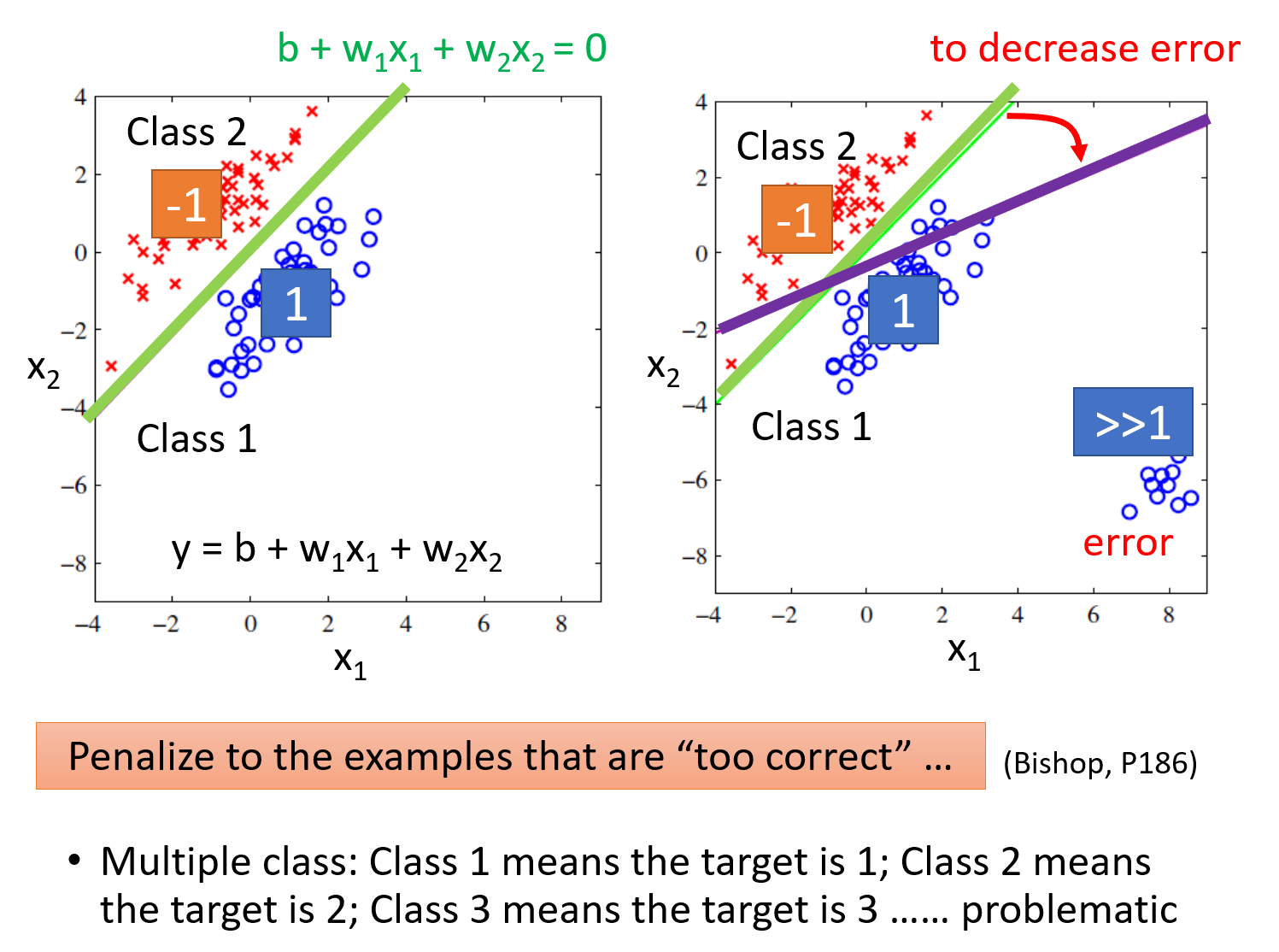
1.2.Ideal Alternatives
理想的方法是这样的:我们要找的function f(x)里面会有另外一个function g(x),当我们的input x输入后,如果g(x)>0,那f(x)的输出就是class 1,如果g(x)<0,那f(x)的输出就是class 2,这个方法保证了function的output都是离散的表示class的数值。

把loss function定义成$L(f)=\sum\limits_n\delta(f(x^n)≠\hat{y}^n)$,即这个model在所有的training data上predict预测错误的次数,也就是说分类错误的次数越少,这个function表现得就越好
但是这个loss function没有办法微分,是无法用gradient descent的方法去解的,当然有Perceptron、SVM这些方法可以用(感知机和支持向量机的内容,在林轩田老师的机器学习基石和技法课程中都有详细的讲解),但这里先用另外一个solution来解决这个问题,即从概率的角度来考虑二分类问题。
2.Solution: Generative model

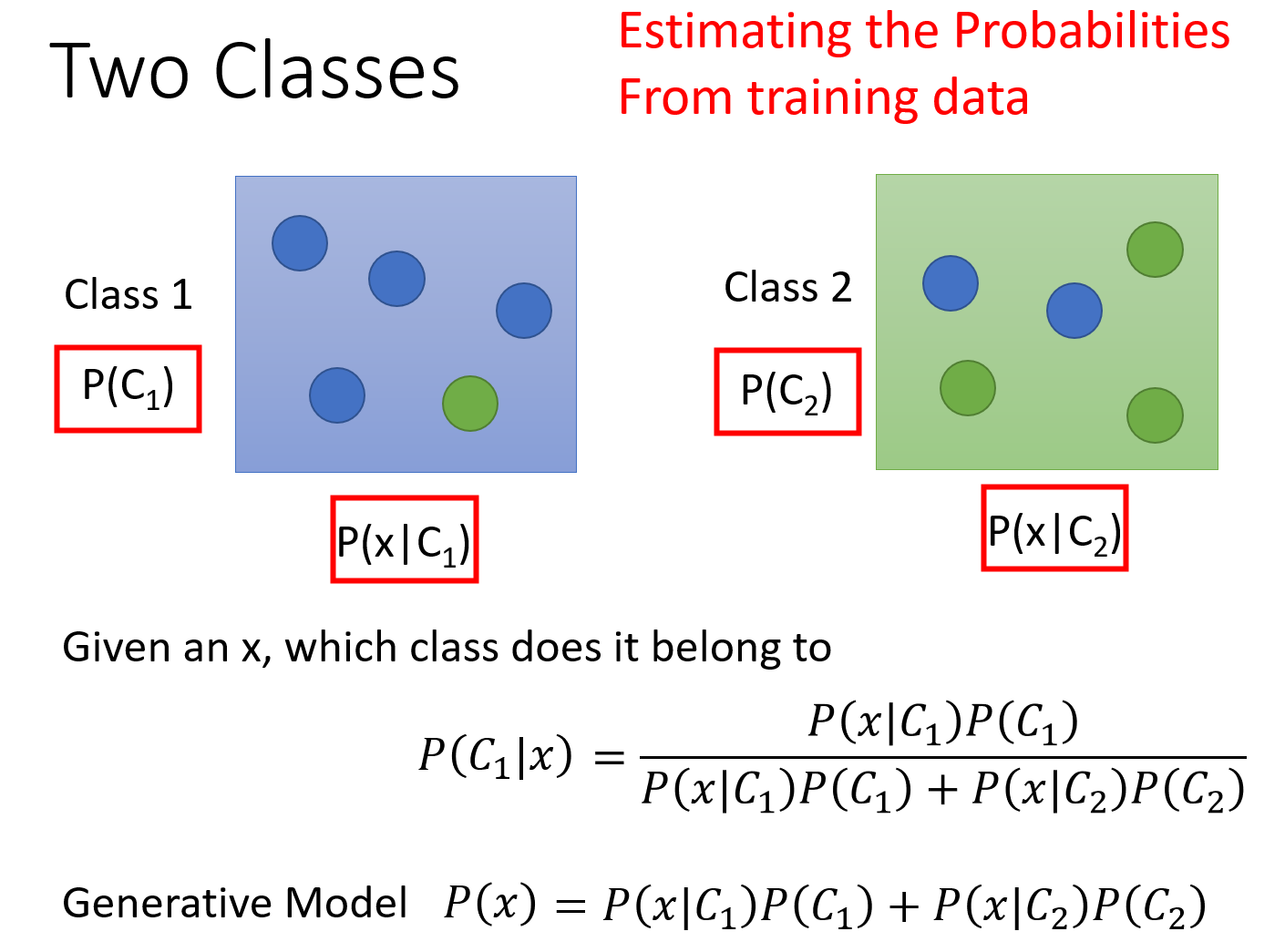
这两张图的内容很好理解,就是贝叶斯公式啦。这种想法叫做Generative model(生成模型),因为有这个model,就可以拿它来generate $x$(如果你可以计算出每一个$x$出现的概率,就可以用这个distribution分布来生成$x$、sample $x$出来)。
接下来考虑怎么计算其中的四项:$P(C_1),P(C_2),P(x|C_1),P(x|C_2)$。
2.1.Prior
$P(C_1)$和$P(C_2)$这两个概率,被称为Prior,计算这两个值还是很简单的。
假设我们还是考虑二元分类问题,编号小于400的data用来Training,编号大于400的data用来testing,如果想要严谨一点,可以在Training data里面分一部分validation出来模拟testing的情况
在Training data里面,有79只水系宝可梦,61只一般系宝可梦,那么$P(C_1)=79/(79+61)=0.56$,$P(C_2)=61/(79+61)=0.44$
2.2.Probability from Class
计算$P(x|C_1)$和$P(x|C_2)$的值,假设$x$是一只新来的海龟,它显然是水系的,但是在79只水系的宝可梦training data里面根本就没有海龟,那要如何计算$P(x|C_1)$呢。
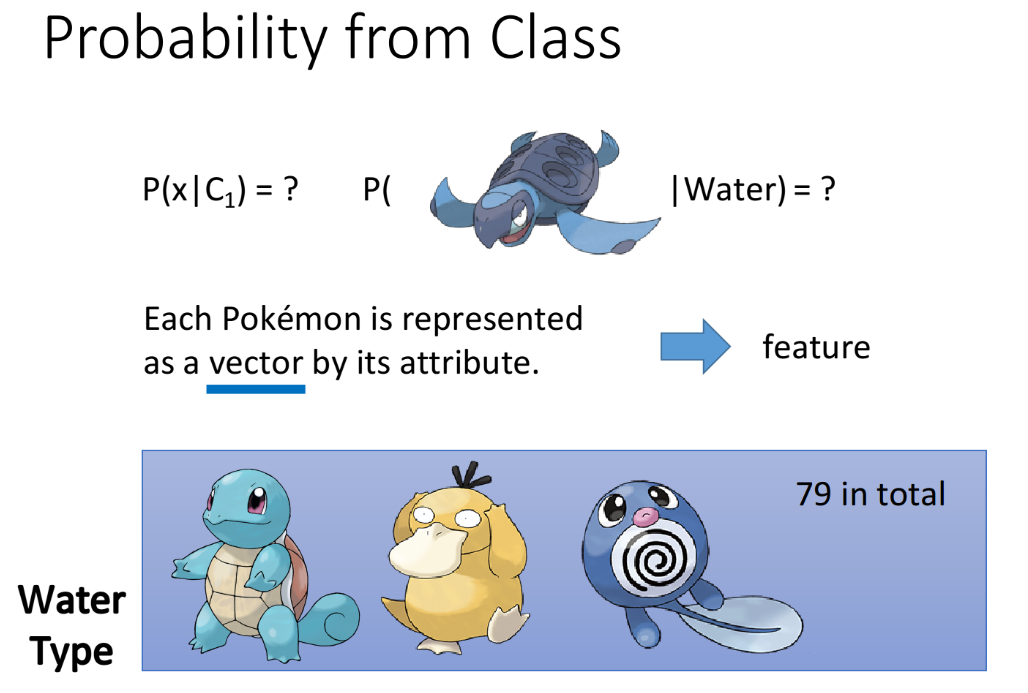
每一只宝可梦可以用由特征值组成的向量来表示,每个sample有7个feature,为了方便可视化,这里只考虑Defense和SP Defence两种feature。我们需要用已有的数据去估测海龟出现的可能性,你可以想象说这已有的79只水系宝可梦的data其实只是冰山一角,假定水系神奇宝贝的Defense和SP Defense是从一个Gaussian的distribution里面sample出来的,下图只是采样了79个点之后得到的分布,但是从高斯分布里采样出海龟这个点的几率并不是0。现在的问题是怎么从这79个已有的点计算出Gaussian distribution函数。
2.3.Gaussian distribution函数
Input: vector $x$, output: probability of sampling x ;其中$\mu$表示方差均值mean,$\Sigma$表示协方差矩阵covariance matrix。
从下图中可以看出,同样的$\Sigma$,不同的$u$,概率分布最高点的地方是不一样的:
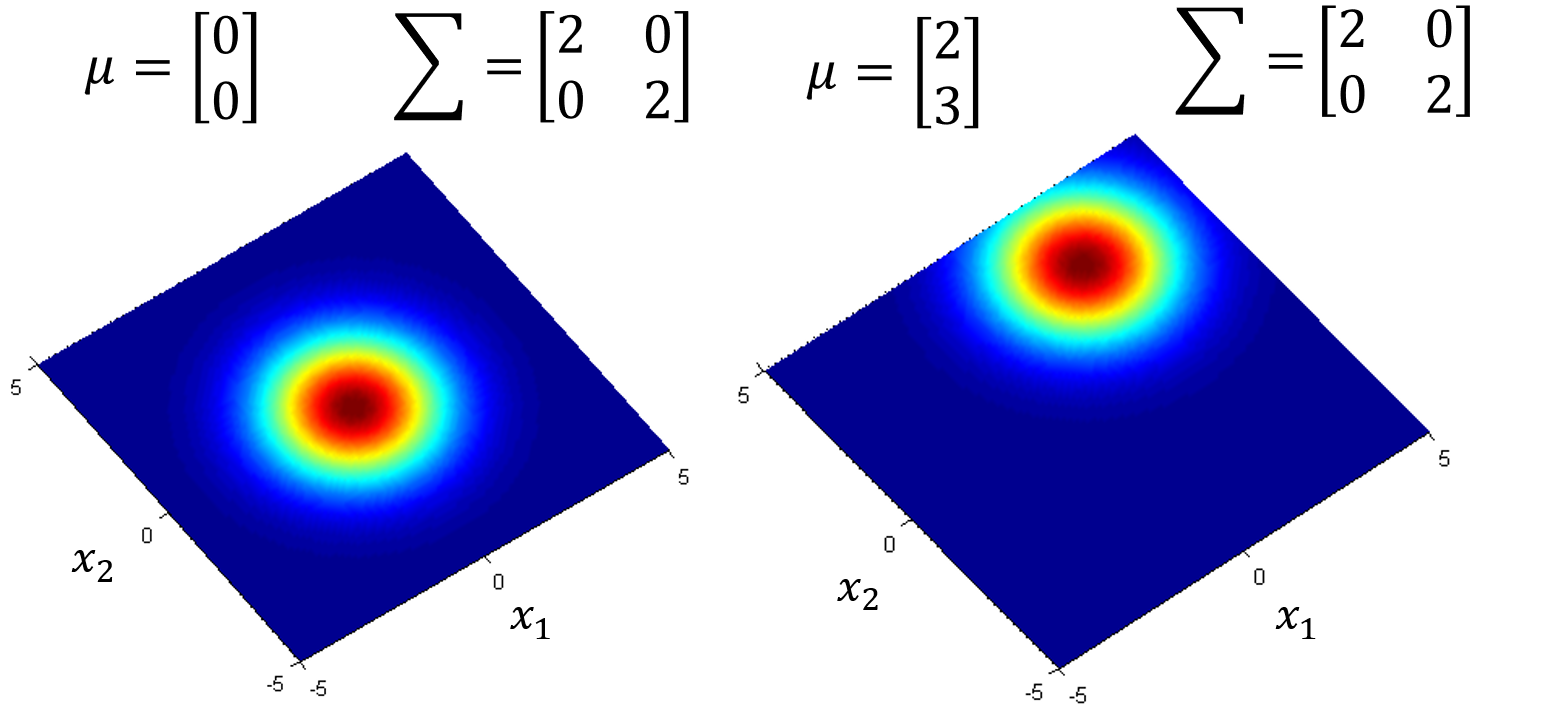
如果是同样的$u$,不同的$\Sigma$,概率分布最高点的地方是一样的,但是分布的密集程度是不一样的:
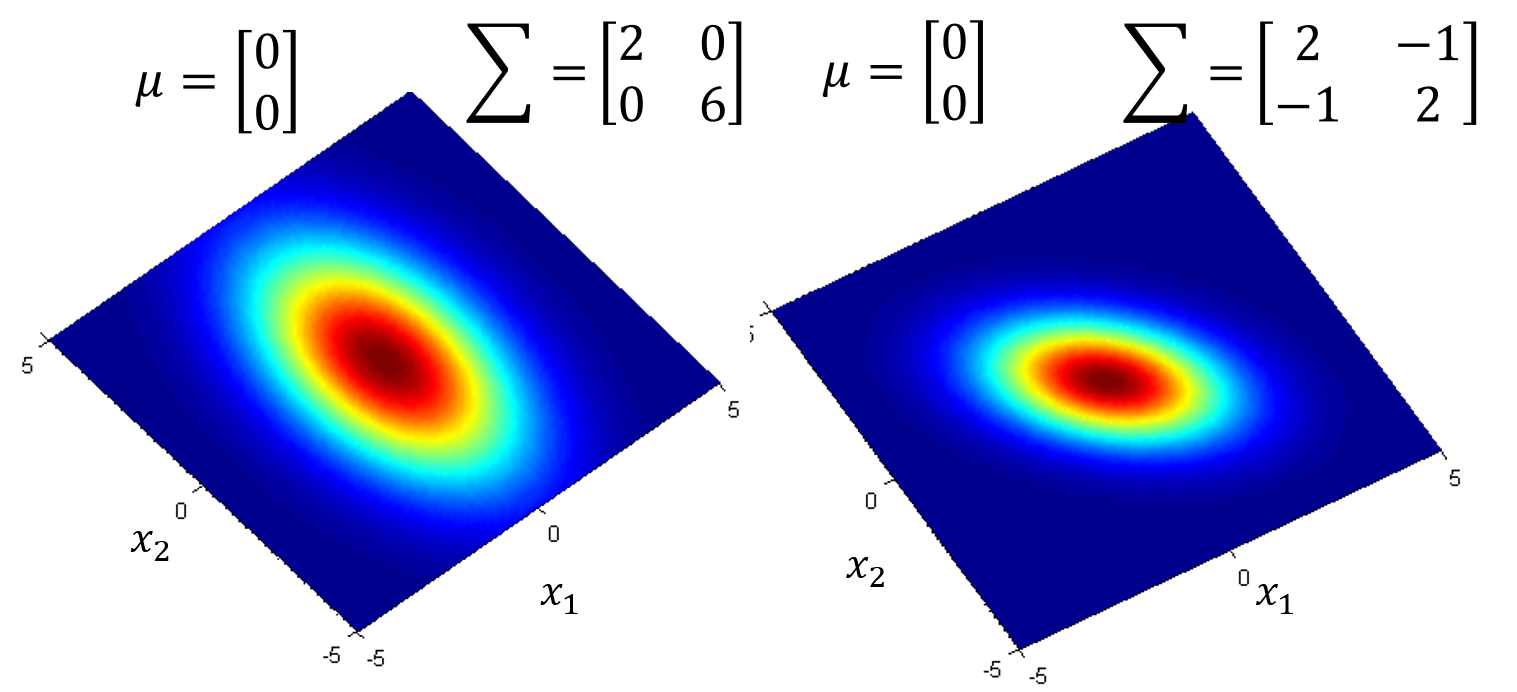
Gaussian distribution函数是由$\mu$和$\Sigma$决定的,估计$\mu$和$\Sigma$可以使用极大似然估计(Maximum Likelihood)的方法,其思路是找出最特殊的那对$u$和$\Sigma$,从它们决定的高斯函数中再次采样出79个点,使”得到的分布情况与当前已知79点的分布情况相同“这件事情发生的可能性最大。
实际上任意一组$u$和$\Sigma$对应的高斯函数($u$表示该Gaussian的中心点,$\Sigma$表示该Gaussian的分散程度)都有可能sample出跟当前分布一致的样本点,就像上图中的两个红色圆圈所代表的高斯函数,但肯定存在着发生概率最大的哪一个Gaussian,而这个函数就是我们要找的。
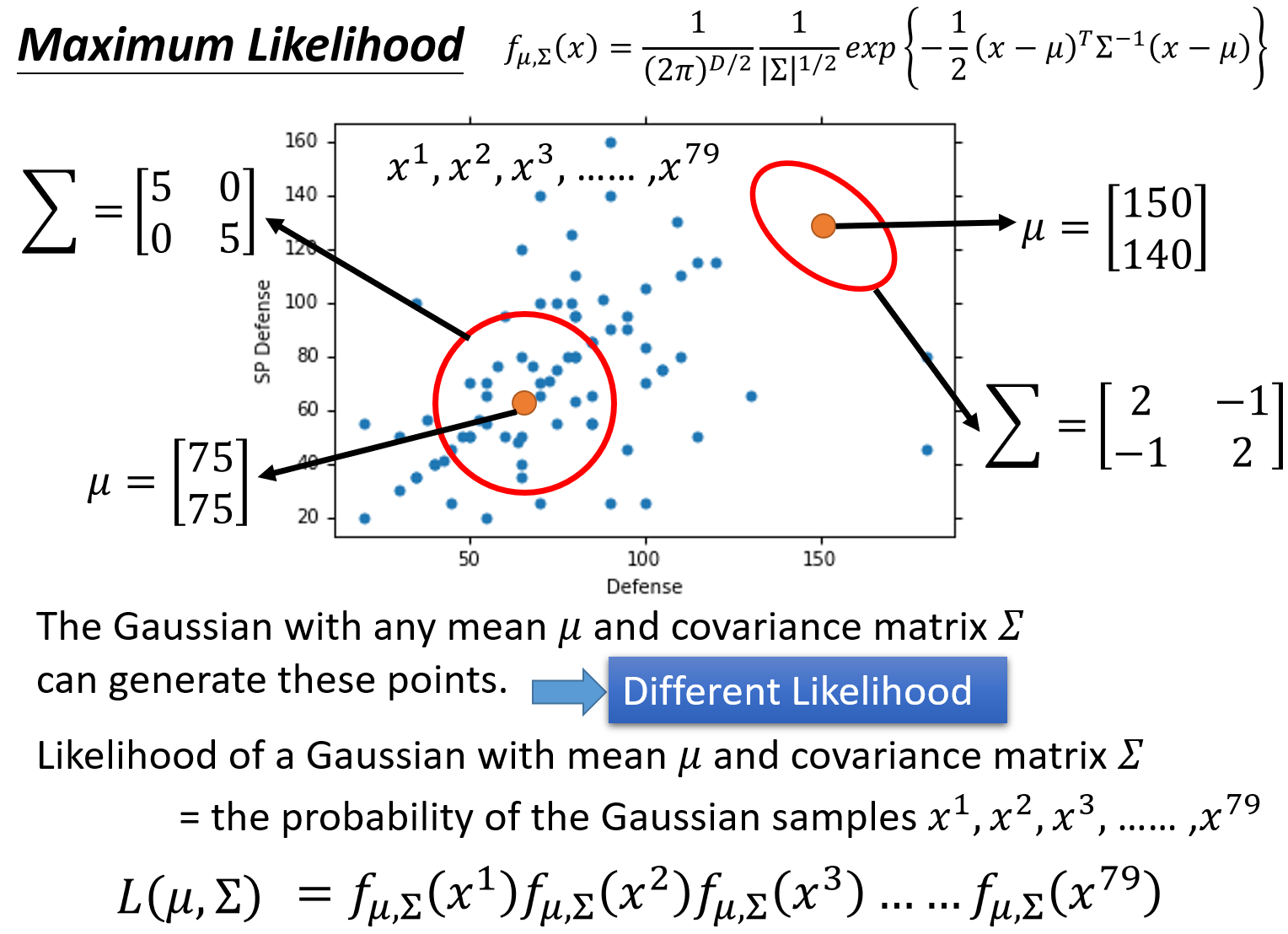
似然函数:
实际上就是该事件发生的概率就等于每个点都发生的概率之积,要求的$\mu$和$\Sigma$就是使似然函数取极大值的$\mu$和$\Sigma$:
对$\mu$和$\Sigma$分别偏导,使微分等于0,得到的高斯函数的$u$和$\Sigma$的最优解如下:
这样我们由Training Data就可以分别求出Class 1和Class 2的$\mu$和$\Sigma$,从而计算出海龟这个sample的$P(x|C_1),P(x|C_2)$。
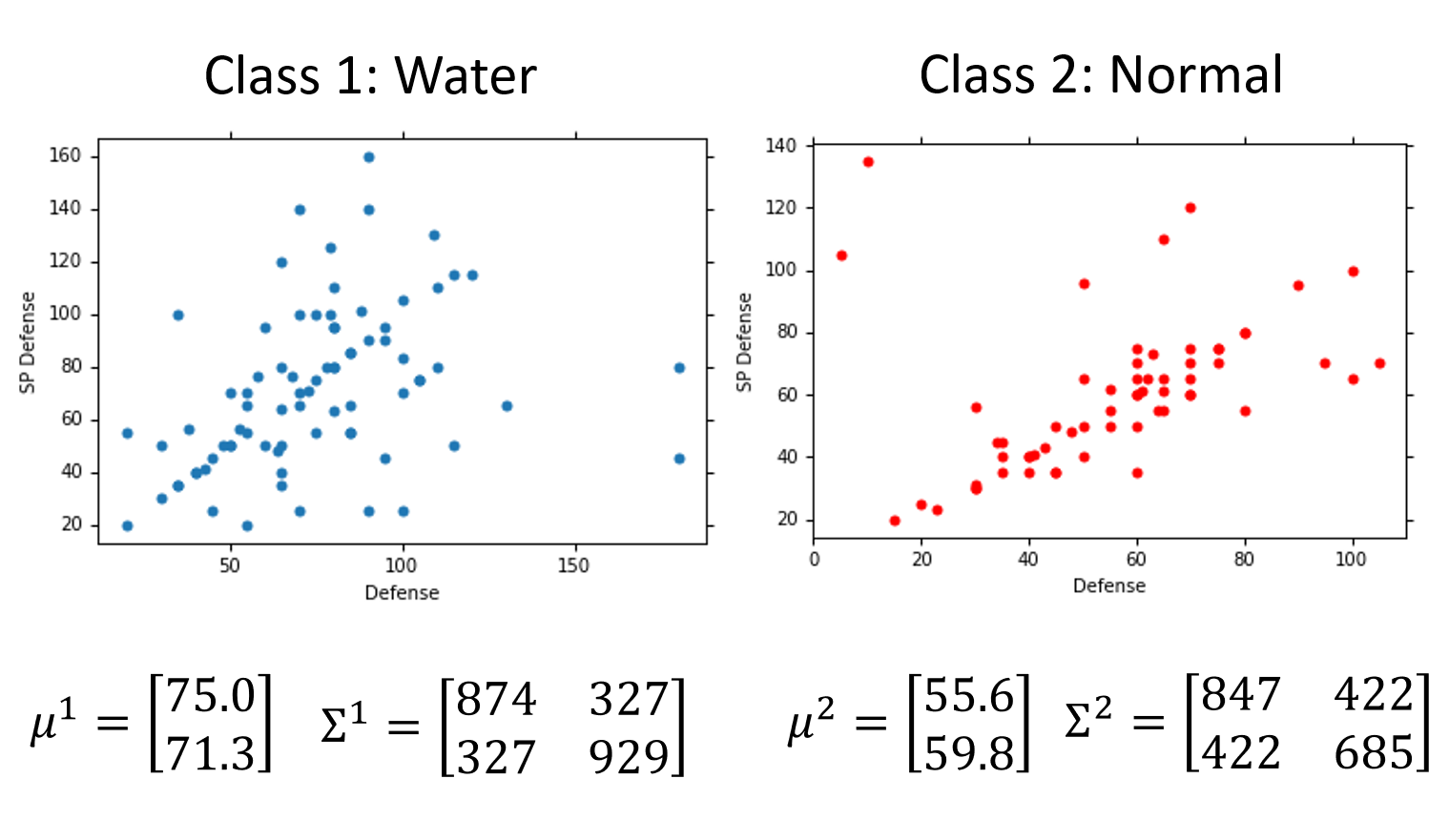
2.4.Do Classification
接着将$P(C_1),P(x|C_1),P(C_2),P(x|C_2)$代入公式计算出$P(C_1|x)$,若大于0.5,则说明sample $x$属于Class 1啦。

将得到的结果在图中表示出来,横轴是Defense,纵轴是SP Defense,蓝色的点是水系的宝可梦的分布,红色的点是一般系的宝可梦的分布,对图中的每一个点都计算出它是class 1的概率$P(C_1|x)$,这个概率用颜色来表示,如果某点在红色区域,表示它是水系宝可梦的概率更大;如果该点在其他颜色的区域,表示它是水系宝可梦的概率比较小
因为我们做的是分类问题,因此令几率>0.5的点为类别1,几率<0.5的点为类别2,也就是右上角的图中的红色和蓝色两块区域,再把testing data上得到的结果可视化出来,即右下角的图,发现分的不是太好,正确率才是47%。
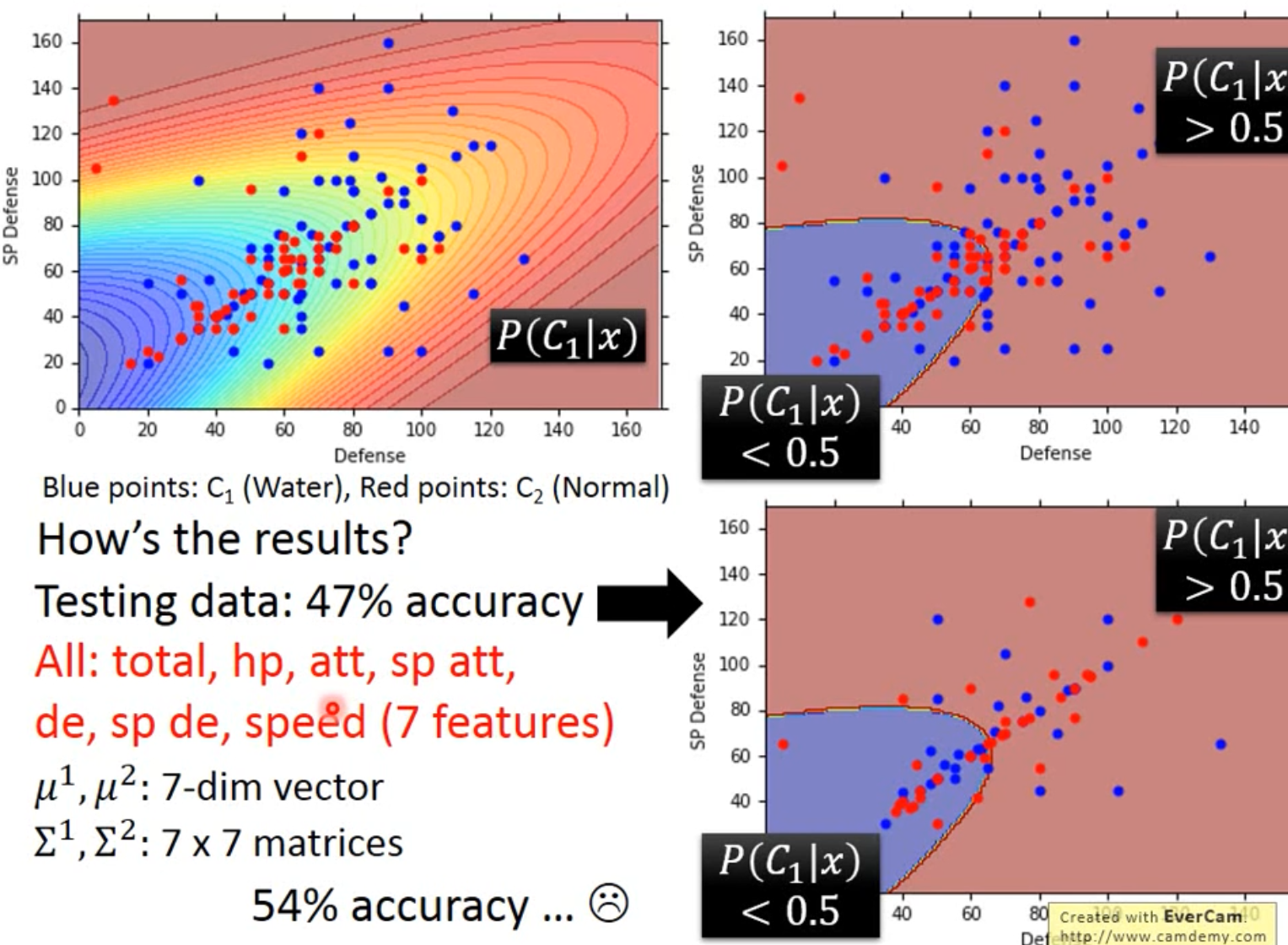
我们之前用的只是Defense和SP Defense这两个feature,在二维空间上得到的效果不太好,但实际上一开始就提到了宝可梦总共是有7个features的,也许在二维空间上它们是重叠在一起的,但是在六维空间上看它们也许会区分得很好。考虑7个feature时,$\mu$是一个7-dim的vector,$\Sigma$则是一个7*7的matrix,发现得到的准确率也才54%,这个分类器表现并不好,接下来考虑如何改进这个分类器。
2.5.Modify Model
上面用到的Gaussian distribution函数,我们给每一个Class的Gaussian都计算了自己的mean和convariance,这种做法其实并不实用,常用的做法是,不同的class可以share同一个cocovariance matrix。variance是跟input的feature size的平方成正比的,所以当feature的数量很大的时候,$\Sigma$大小的增长是可以非常快的,在这种情况下,给不同的Gaussian以不同的covariance matrix,会造成model的参数太多,而参数多会导致该model的variance过大,出现overfitting的现象,因此对不同的class使用同一个covariance matrix,可以有效减少参数,减小overfitting。
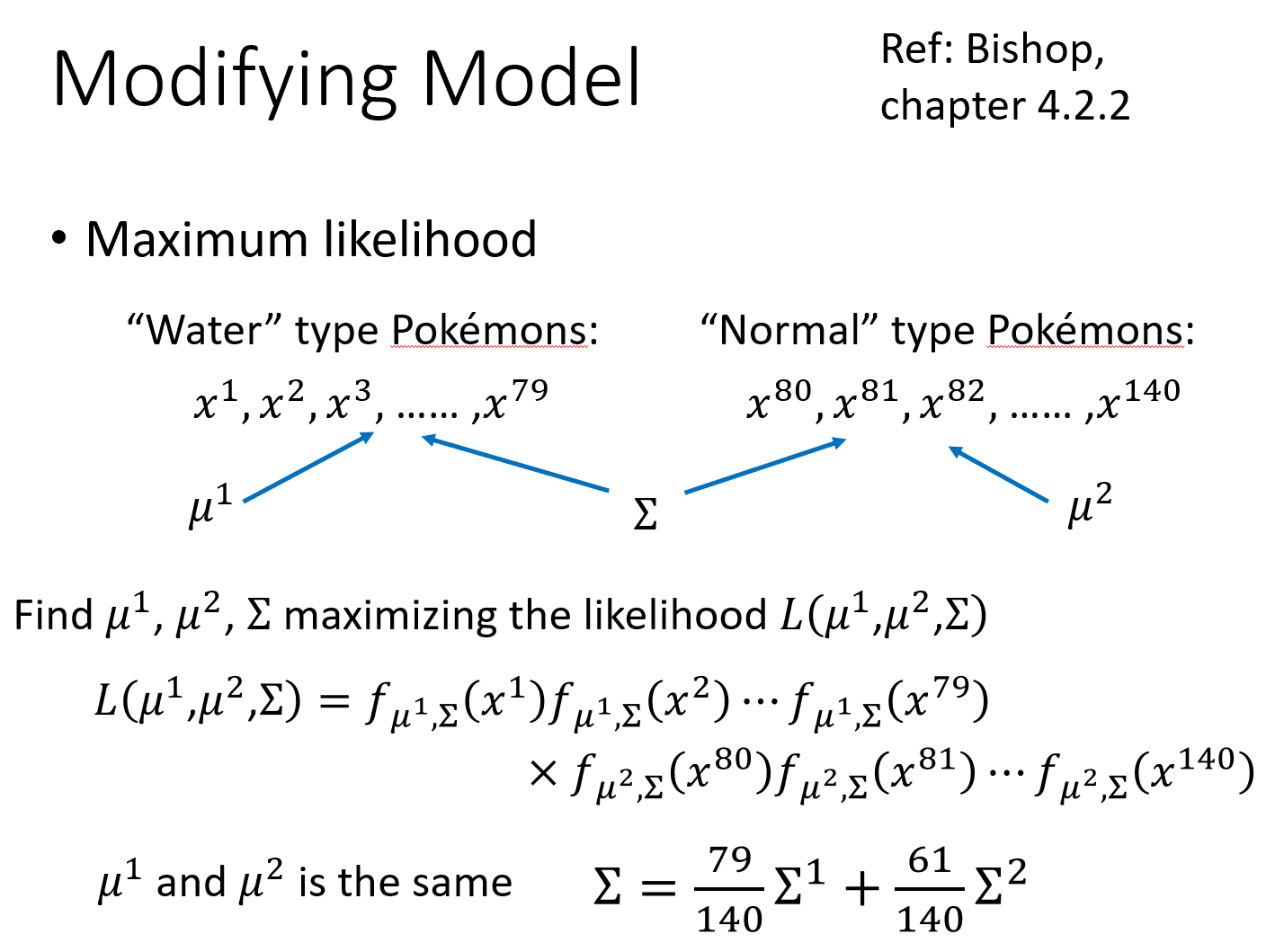
这样用$\mu_1$、$\mu_2$和$\Sigma$来决定一个总的似然函数,求出其取极大值时的$\mu_1$、$\mu_2$和$\Sigma$,发现得到的$u_1$和$u_2$和原来一样,还是各自的均值,而$\Sigma$则是原先两个$\Sigma_1$和$\Sigma_2$的加权。
将结果表示在图中,你会发现,class 1和class 2在没有共用covariance matrix之前,它们的分界线是一条曲线;如果共用covariance matrix的话,它们之间的分界线就会变成一条直线,这样的model,我们也称之为linear model(尽管Gaussian不是linear的,但是它分两个class的boundary是linear)。
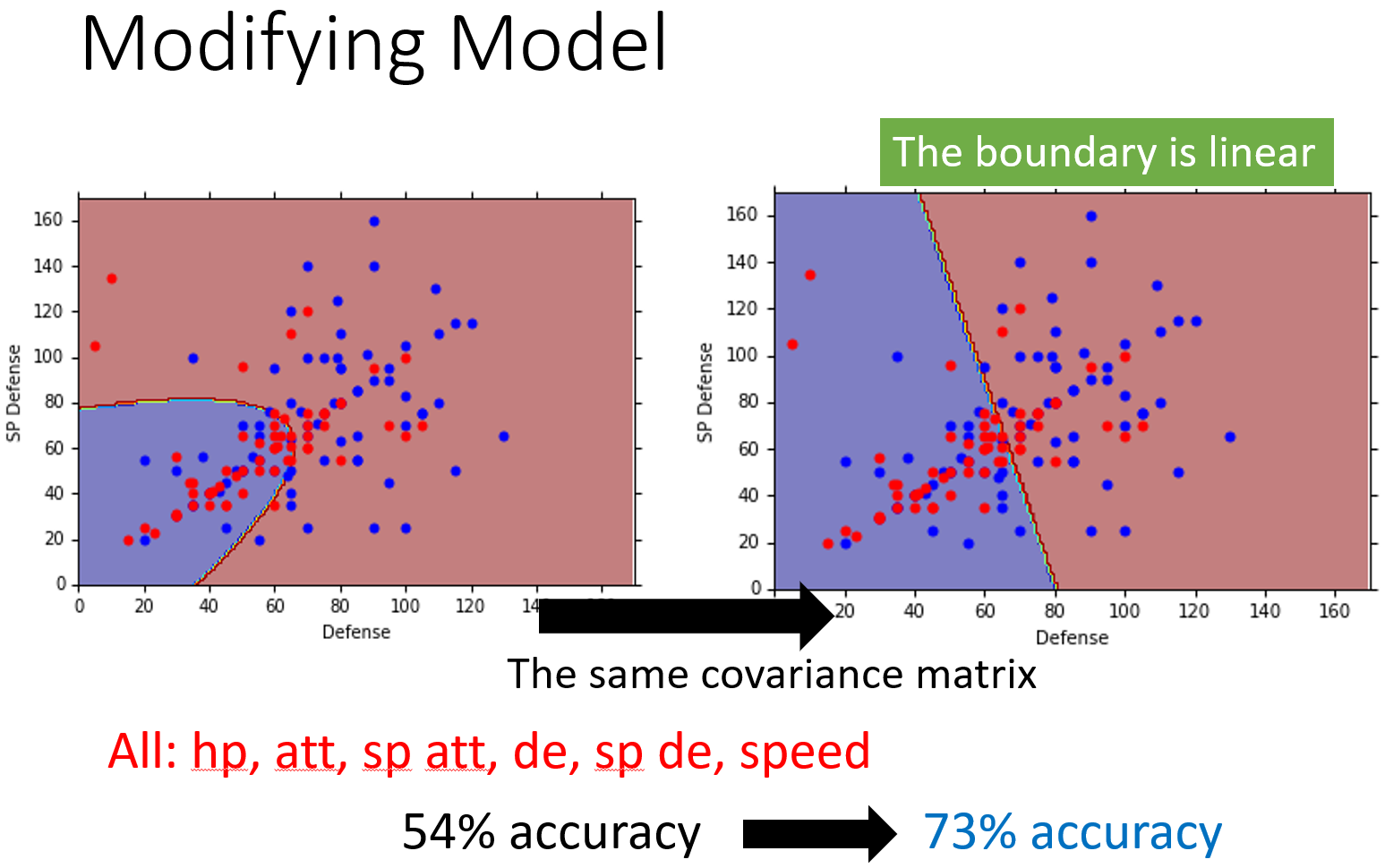
如果考虑宝可梦的所有的7个feature,且共用covariance的话,正确率会从原来的54%提升到73%。
2.6.Three Steps of classification
回顾一下做classification的三个步骤,实际上也就是做machine learning的三个步骤:
Find a function set(model)
这些required probability $P(C)$和probability distribution $P(x|C)$就是model的参数,选择不同的Probability distribution(比如不同的分布函数,或者是不同参数的Gaussian distribution),就会得到不同的function,把这些不同参数的Gaussian distribution集合起来,就是一个model,如果不适用高斯函数而选择其他分布函数,就是一个新的model了
当这个posterior Probability $P(C|x)>0.5$的话,就output class 1,反之就output class 2
Goodness of function
对于Gaussian distribution这个model来说,要评价的是决定这个高斯函数形状的均值$u$和协方差$\Sigma$这两个参数的好坏,而极大似然函数$L(u,\Sigma)$的输出值,就评价了这组参数的好坏
Find the best function
找到的那个最好的function,就是使$L(u,\Sigma)$值最大的那组参数,实际上就是所有样本点的均值和协方差:
式中的$x$表示一个feature的vector,上标$i$表示第$i$个sample

2.7.Probability distribution
上面的讨论中我们使用的是Gaussian distribution函数,当然你也可以使用其他分布函数,这通常要根据数据集的具体情况来确定,比如一个特征是binary feature,那选择使用伯努利分布Bernoulli distribution比较好。如果选择的是简单的分布函数(参数比较少),那么bias就偏大,variance就小;如果选择复杂的分布函数,那么bias就偏小,variance就偏大。
Naive Bayes Classifier(朴素贝叶斯分类法)
考虑这样一件事情,假设$x=[x_1 \ x_2 \ x_3 \ … \ x_k \ … \ ]$中每一个dimension $x_k$的分布都是相互独立的,它们之间的covariance都是0,那我们就可以把x产生的几率拆解成$x_1,x_2,…,x_k$产生的几率之积。

这里每一个dimension的分布函数都是一维的Gaussian distribution,就相当于原高维的Gaussian,它的covariance matrix变成是diagonal(对角的),在不是对角线的地方,值都是0,这样就可以更加减少需要的参数量,就可以得到一个更简单的model。
这种方法叫做Naive Bayes Classifier(朴素贝叶斯分类法),如果真的明确了所有的feature之间是相互独立的,是不相关的,使用朴素贝叶斯分类法的performance是会很好的;如果这个假设是不成立的,那么Naive bayes classfier的bias就会很大,它就不是一个好的classifier(朴素贝叶斯分类法本质就是减少参数)。
在宝可梦这个例子中(李老师也是个老二次元了|ू・ω・` )),使用朴素贝叶斯的效果并不好,因为不同feature之间还是有相关的,各种feature之间的covariance还是必要的,比如战斗力和防御力它们之间是正相关的,covariance不能等于0。
2.8.Analysis Posterior Probability
接下来我们来分析一下这个后置概率的表达式,会发现一些有趣的现象
表达式上下同除以分子,再引入变量$z$,得到$\sigma(z)=\frac{1}{1+e^{-z}}$,这个function叫做sigmoid function

sigmoid函数真是再熟悉不过了,接下来推导一下$z$的具体表达式,Warning of Math(老师原话:下面这部分推导听不懂的同学可以先睡一会⊙(・◇・)?,之后直接听结论)



推导是有些复杂,但当$\Sigma_1$和$\Sigma_2$相同时,经过化简$z$就变成了一个linear的function,$x$前的一项可以当做vector $w$,后面的几项相加是一个scalar,当做常数$b$。

$P(C_1|x)=\sigma (w\cdot x+b)$这个式子就解释了,当class 1和class 2共用$\Sigma$的时候,它们之间的boundary会是线性的。
这样在Generative model里,我们要做的就是用某些方法去找出$N_1,N_2,u_1,u_2,\Sigma$,找出这些以后就算出$w$和$b$,把它们代进$P(C_1|x)=\sigma(w\cdot x+b)$这个式子,计算概率。
但是为什么要这么麻烦呢(キ`゚Д゚´)?我们的最终目标都是要找一个vector $w$和const $b$,何必先去计算概率,算出一些$u,\Sigma$,然后再回过头来又去算$w$和$b$。那么能不能直接把$w$和$b$计算出来呢,下一节课Logistic Regression将会解决这个问题。