Background Konwledge:
- $\mu$-strong convexity
- Lipschitz continuity
- Bregman proximal inequality
这一节课会比较概念上的讲解Optimization for Deep Learning这个主题,不会去详细证明每个算法在某些情况能达到convergence。
明确几个Notations:
- $\theta_t$:model parameters at time step $t$
- $\nabla L(\theta_t) $ or $g_t$:gradient at $\theta_t$, used to compute $\theta_{t+1}$
- $m_{t+1}$:momentum accumulated form time step 0 to time step t, which is used to compute $\theta_{t+1}$(可以理解为momentum记录了time step 0到t的梯度信息)
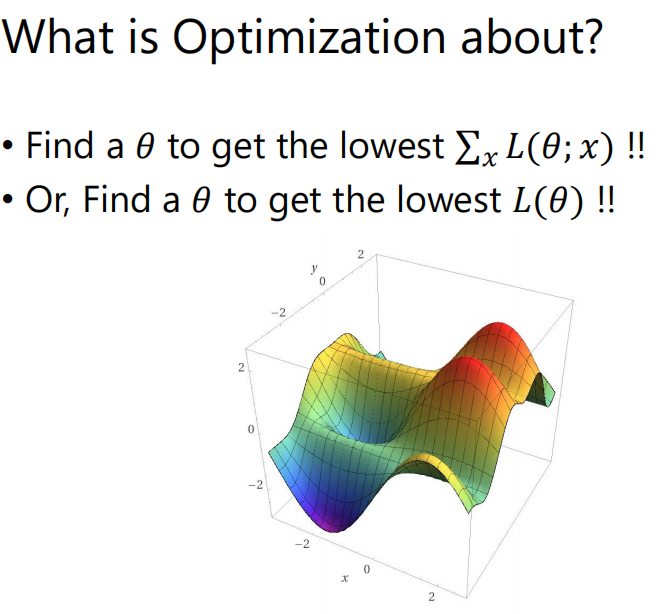
我们先要考虑对一个神经网络做Optimization是要做什么,就是要找到一组参数$\theta$使得training data中所有的x算出来的loss之和最小,即让神经网络越贴近训练资料越好,把一个$x_t$输入到神经网络中得到的$y_t$越接近$\hat y_t$越好;或者如果用特定的$x$,那我们就是要找在loss surface上的最小值。
On-line vs Off-line
- On-line: one pair of $(x_t, \hat y_t)$ at a time step
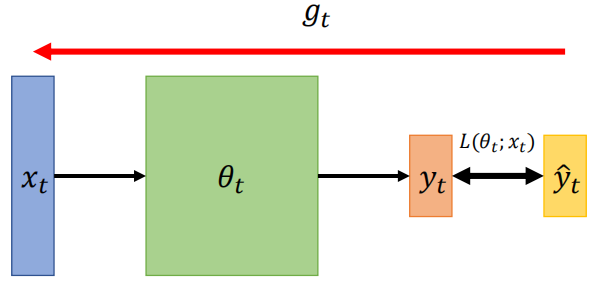
- Off-line: pour all $(x_t,\hat y_t)$ into the model at every time step
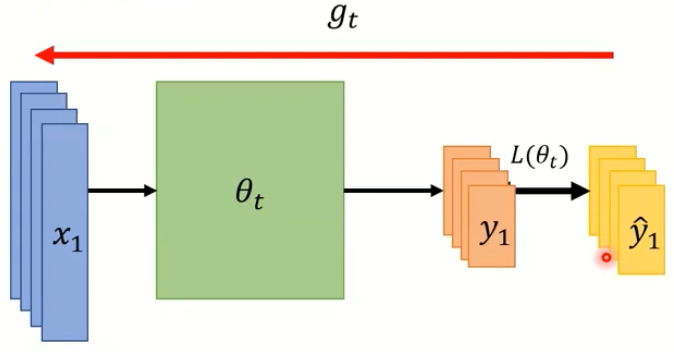
显然Off-line learning的训练方式会更好,我们一次可以看到所有的training data,但由于电脑硬件的限制等因素Off-line实际实施起来却有困难。但这节课中我们先暂且抛开这些因素,只关注Off-line的cases。
回顾之前讲过的几种优化算法(具体可以看之前的笔记):
SGD(Stochastic Gradient Descent,随机梯度下降)
SGD with momentum
- Adagrad
- RMSProp
- Adam
来看一下提出这些方法的时间:

Optimizers: Real Application
大家听过的很多著名的深度学习模型,比如NLP领域的BRET(Bidirectional Encoder Representation from Transformers,是一个预训练的语言表征模型),Transformer(sequence to sequence模型),Tacotron(端到端语言合成模型);Big-GAN(图像生成模型);MAML(Model-Agnostic Meta-Learning)都是用ADAM训练出来的。又如CV领域的YOLO(目标检测),Mask R-CNN(对象实例分割框架),ResNet(深度残差网络,用于图片分类)则是用到SGDM 。
那这些很知名的model都是用这些14年以前提出的optimizer来训练的呢,可以说是因为ADAM和SGDM已经做得非常好了,后面提出的optimizer都是去填补它们俩中间的空白,并没有很明显的超越,如下面几张图中的例子。
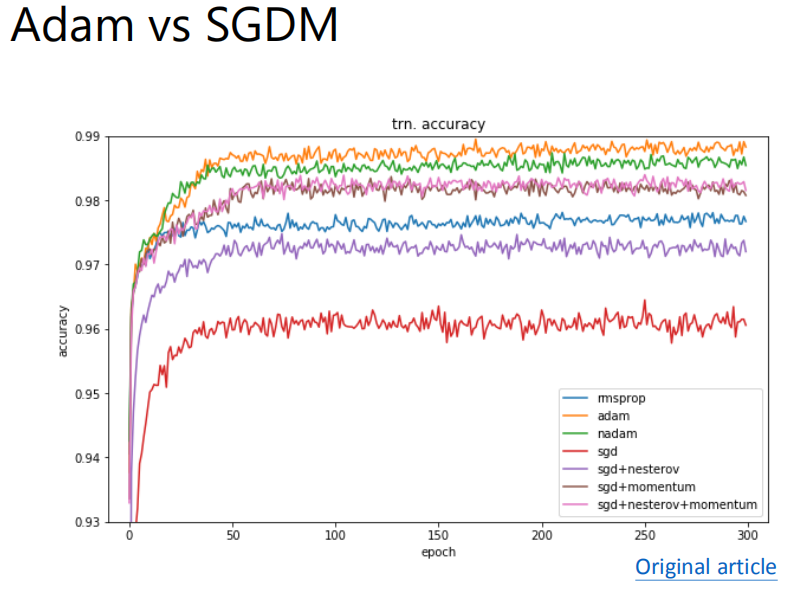
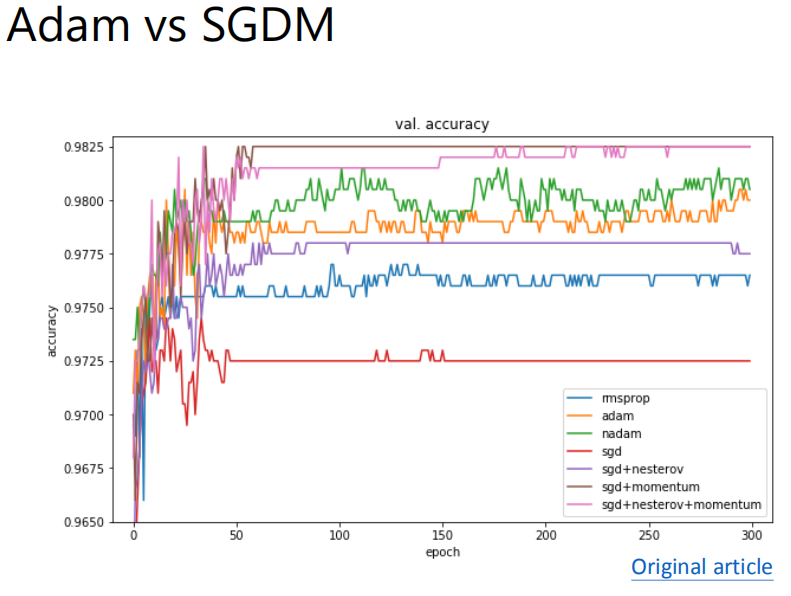
Adam和SGDM是有一定的差别的:
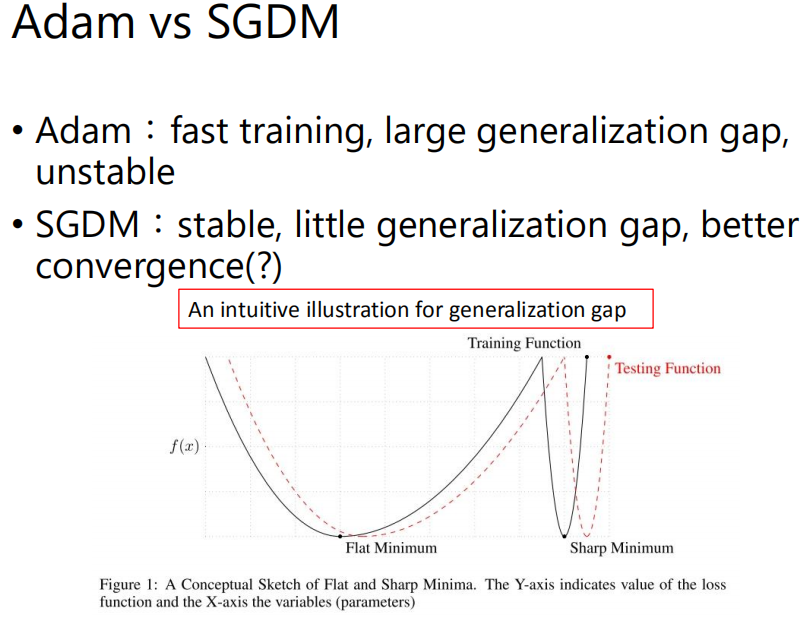
Adam的generalization能力比较差,在testing data上的落差比较大;而SGDM的generalization能力比较好,在testing data上的落差比较小。
先来直观地理解一下generalization gap,上图中的黑色实线是Training loss function,红色虚线是Testing function,因为Training data和Testing data的分布有差异,所以它们的loss function可能会有点像,但也有差距。有两个值相同的Minimum,如果找到一个比较平坦的Minimum,那两个function在这里都比较平坦,差距会比较小;如果找到一个比较sharp的Minimum,两个function在这里都比价陡,差距会比较大。那造成Adam和SGDM在generalization上的差异的一个可能的原因就是Adam比较会找到Sharp Minimum,而SGDM比较会找到Flat Minimum,当然也还有其他的原因。
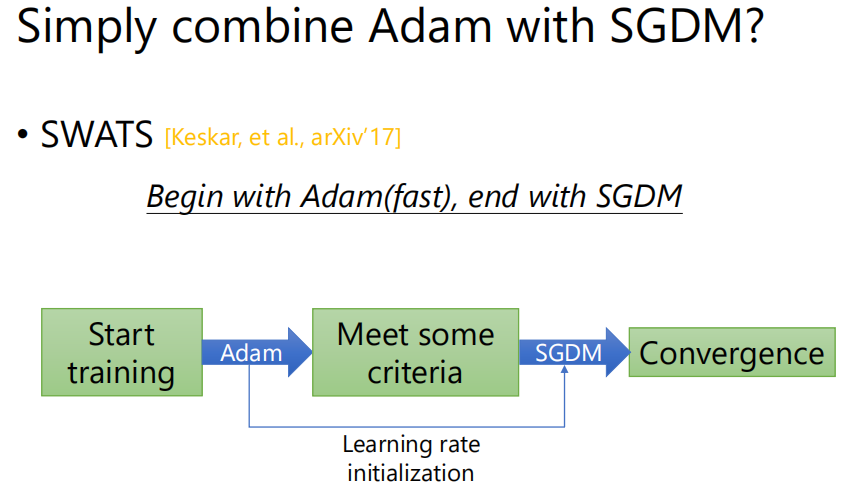
既然Adam比较快,SGDM比较稳,而且可以收敛到比较小的值,那就有人提出将这两种方法结合—SWATS。训练的前半部分用Adam,后半部分用SGDM,但论文中Adam和SGDM切换的点的设置并不是很科学。
那我们有没有办法来修正Adam,让Adam像SGDM一样收敛的又稳又好呢。先来考虑Adam存在什么问题,
首先我们假设公式中的$\beta_1=0$,只关注adaptive learning rate,即分母$v_t$那一项的影响。设$\beta_2=0.999$,那$v_t$会受到gradient的影响大概就有$1/(1-0.999)=1000$个step那么久。论文[Reddi, et al., ICLR’18里写到在training的最后阶段,大部分的gradient都会很小,且对descent的方向不能提供什么有用的信息。只有某几个minibatch的gradient会很大,会较明确地告诉参数应该往哪个方向update。那基于这一事实,在做Adam的时候会出现问题呢。

假设已经training了10W个step,10W之后的几个step的gradient都很小,比如说都是1;直到过了1000个step后突然出现一个很大的gradient,如100000;下一个step,gradient会变得很小,比如1。
考虑第100000个step,由于我们假设$\beta_1=0$,那$m_t$就等于gradient的大小;假设前面在这之前的step的gradient有很多1,这时分母$\sqrt{\hat v_t}+\varepsilon$也是1 ,那这一步的movement就是$\eta$;之后几个step也是如此。当gradient为100000的step,$m_t=g_t=10^5$,$\sqrt{\hat v_t}+\varepsilon=\sqrt{0.001\cdot(10^5)^2}=10^{3.5}$,那movement就是$10\sqrt{10}\eta$。到下一个step,gradient=1,movement=$10^{-3.5}\eta$。那这会发生什么问题呢?

可以看到前面这1000个step它们提供的movement是$1000\eta$,而之后这个gradient=10W的真正有意义的step,它只会移动$10\sqrt{10}\eta \approx 30\eta$,可见真正提供比较多信息的gradient它在update的时候只能造成很小的影响。当前面gradient比较小的时候,network可能不知道后面会出现有很大的gradient,就以为现在的gradient已经不错了,结果造成了不好的影响。并且movement的大小是有上限的,为$\sqrt{\frac{1}{1-\beta_2}}\eta$。所以当大部分的gradient都很小,真正有意义的gradient的作用就会受影响。
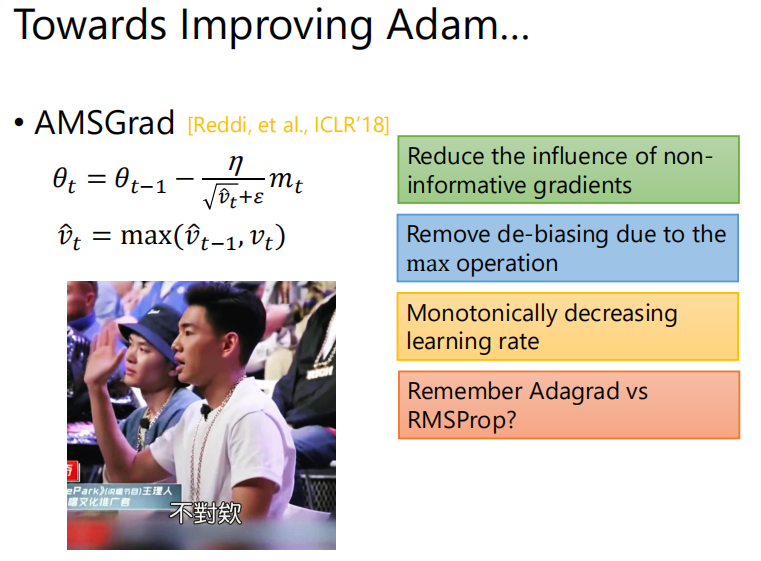
作者提处的方法叫AMSGrad,目标就是减小这些无意义的gradient的影响,做法是令$\hat v_t=\max(\hat v_{t-1},v_t)$。上面的例子来说明就是,假设在10W步之前出现过很大的gradient,但走到10W步这里已经忘了,给很小的gradient的step也走的比较大,那后面遇到很大的gradient反而会走的很小。作者的思路就是通过max operation来记住过去最大的$v_t$。
记得之前我们有讲过Adagrad的表达式,$w^{t+1}=w^t-\frac{\eta}{\sqrt{\sum\limits_{i=0}^t(g^i)^2}}\cdot g^t$,它会因为分母一直变大,导致learning rate一直减小,这是要解决的问题。那到AMSGrad这里反而后绕了回来,让分母变大,那可能AMSGrad并不是一个很好的解法。
下面来看另外一篇论文[Luo, et al., ICLR’19]提供的解决思路。

AMSGrad只考虑了解决learning rate很大的情况,这篇论文的作者的方法AdaBound,也考虑在gradient很大的时候,让learning rate不会很小。他将$\frac{\eta}{\sqrt{\hat v_t}+\varepsilon}$做了一个clip(将这一项的值限制在一个最小值和最大值之间),但这个有点经验公式的意味,且这个最小值和最大值和loss并没有什么关系,不太符合我们做Adaptive learning rate的期望。

那我们现在换个角度,来看一看对SGDM可以做哪些调整。SGDM的优点是稳定,收敛得好,但它运算得很慢,造成这的原因是它每次update的时候用的是固定的learning rate,而不想Adaptive leaning rates的算法那样可以动态地调整learning rates的大小。

然而SGDM是无法做到learning rate的,那可不可以帮SGDM找一个最佳的learning rate呢,这个learning rate收敛得比较快,让SGDM的结果比较接近Adam。
我们在调learning rate的时候常会有这样的经验,当learning rate最小或最大的时候,结果都不会太好;一定是当learning rate适中的时候会得到较好的performance。
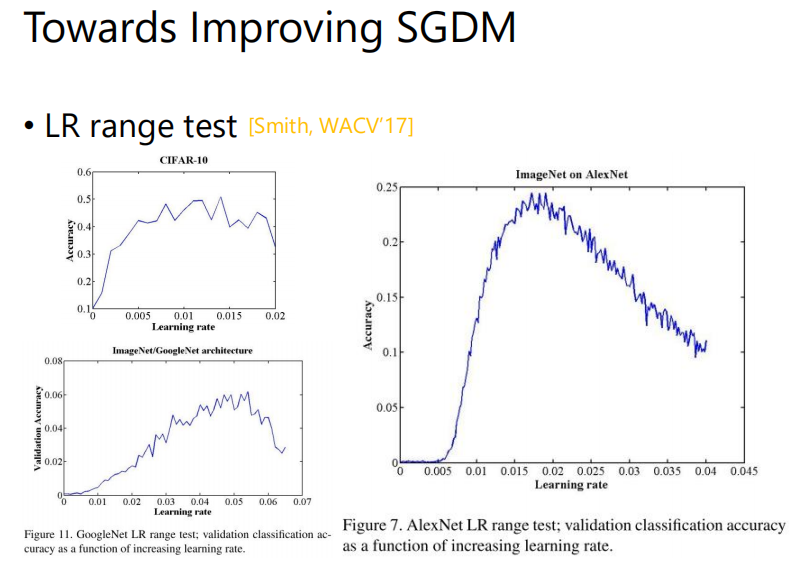
在论文[Smith, WACV’17]里面,作者提出了Cyclical LR,让learning rate在大小大小地周期性变化。learning rate大的时候就相当于做一个forward的动作,learning rate小的时候就相当于做一个fine tune或者是收敛的动作。通常我们在做的时候,learning rate会不断变小,这里让Learning rate变大其实是鼓励这个model“不要满足现状”,在适当的时候做更多尝试。这里有一些参数要决定:step size,以及最大和最小的learning rate。

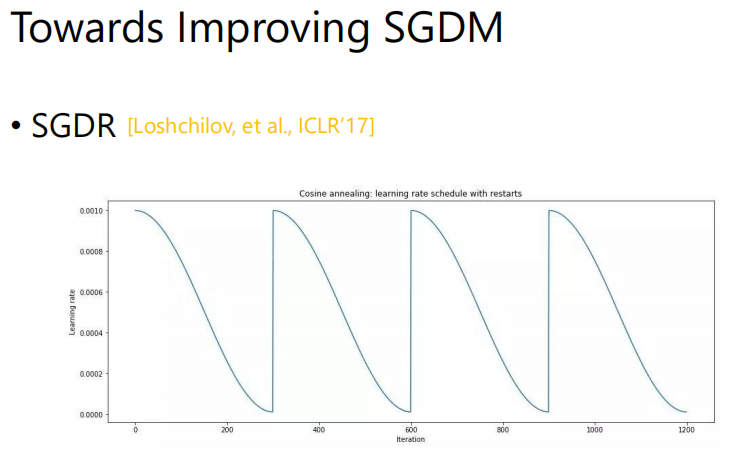
下面是一个很类似的做法SGDR[Loshchilov,et al., ICLR‘17],只是调整learning rate的方法不一样。
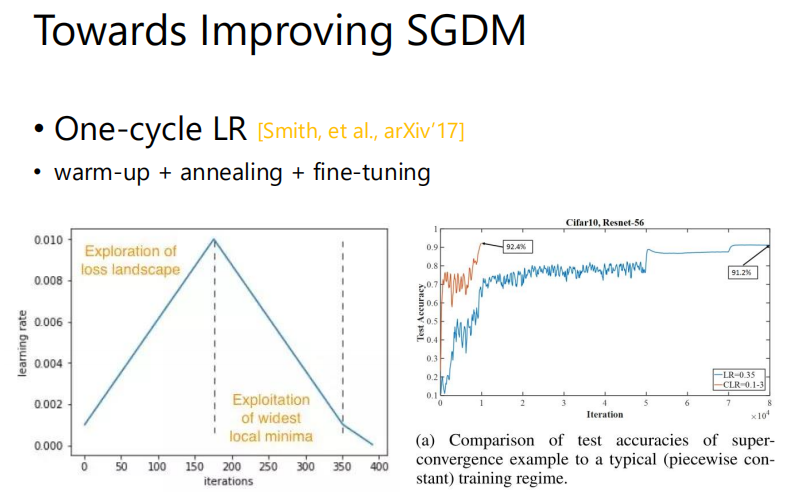
另一个方法One-cycle LR的思想是只做一个cycle,分为三个阶段:warm up—learning rate逐渐增大,直到找到一个还不错的minima附近;annealing—learning rate逐渐减小;fine-tuning—收敛。
那你可能会想Adam需要这样的三个过程嘛,比如Adam需要warm up嘛,有人也做了这方面的研究