DL笔记（11）Unsupervised Learning-PCA

1.Unsupervised Learning

无监督学习(Unsupervised Learning)可以做的事大致分为两种：

• “化繁为简”
  • 聚类(Clustering)
  • 降维(Dimension Reduction)
• “无中生有”：Generation

对于无监督学习(Unsupervised Learning)来说，我们通常只会拥有$(x,\hat y)$中的$x$或$\hat y$，其中：

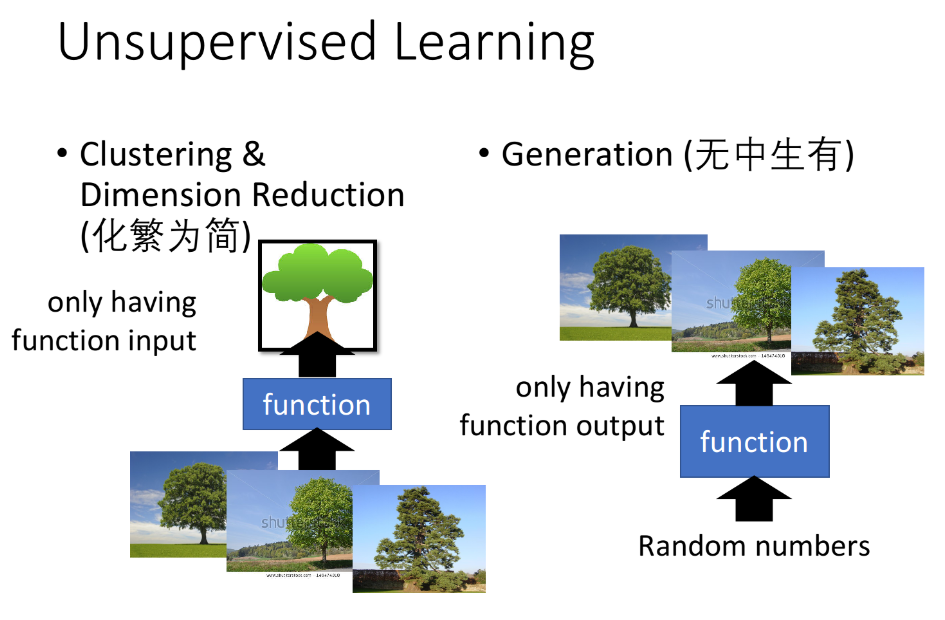
• 化繁为简就是把复杂的input变成比较简单的output，比如把一大堆没有打上label的树图片转变为一棵抽象的树，此时training data只有input $x$，而没有output $\hat y$；
• 无中生有就是随机给function一个数字，它就会生成不同的图像，此时training data没有input $x$，而只有output $\hat y$。

下面我们先简单介绍下Clustering，然后focus在dimension reduction上，而且只focus在linear dimension reduction上。

2. Clustering

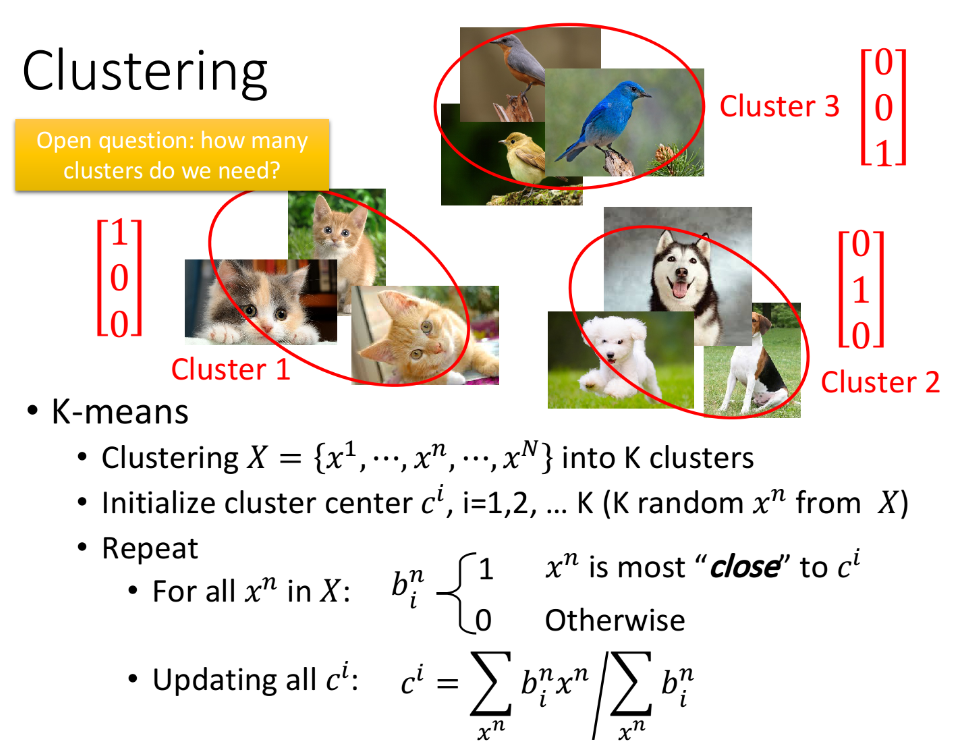
Clustering（聚类），顾名思义，就是把相近的样本划分为同一类，比如对下面这些没有标签的image进行分类，手动打上cluster 1、cluster 2、cluster 3的标签，这个分类过程就是化繁为简的过程。那有一个很critical的问题：我们到底要分几个cluster？

2.1. K-means

最常用的聚类方法是K-means：

• 我们有一大堆的unlabeled data $\{x^1,…,x^n,…,x^N\}$，我们要把它划分为K个cluster；
• 对每个cluster都要找一个center $c^i,i\in \{1,2,…,K\}$，initial的时候可以从training data里随机挑K个object $x^n$出来作为K个center $c^i$的初始值；
• 遍历所有的object $x^n$，并判断它属于哪一个cluster，如果$x^n$与第i个cluster的center $c^i$最接近，那它就属于该cluster，我们用$b_i^n=1$来表示第n个object属于第i个cluster，$b_i^n=0$表示不属于；
• 更新center：把每个cluster里的所有object取平均值作为新的center值，即$c^i=\sum\limits_{x^n}b_i^n x^n/\sum\limits_{x^n} b_i^n$；
• 重复进行以上的操作；

注：如果不是从原先的data set里取center的初始值，可能会导致部分cluster没有样本点。

2.2. HAC

HAC（Hierarchical Agglomerative Clustering，层次聚类）。假设现在我们有5个样本点，想要做clustering：

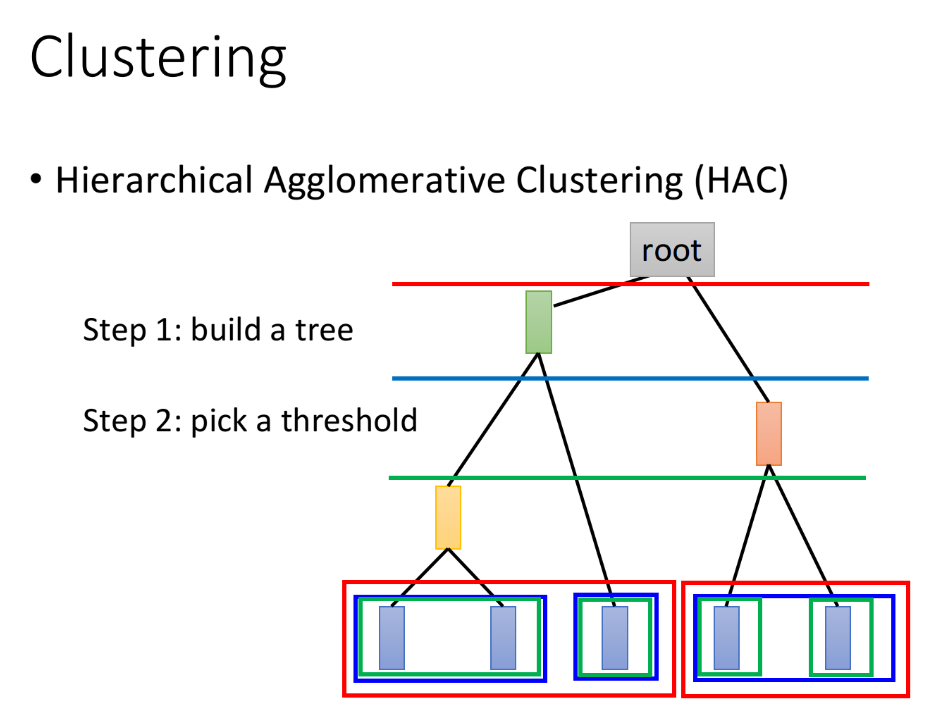
• build a tree:

  （整个过程类似建立Huffman Tree，只不过Huffman是依据词频，而HAC是依据相似度建树）

  • 对5个样本点两两计算相似度，挑出最相似的一对，比如样本点1和2；
  • 将样本点1和2进行merge (可以对两个vector取平均)，生成代表这两个样本点的新结点；
  • 此时只剩下4个结点，再重复上述步骤进行样本点的合并，直到只剩下一个root结点。

• pick a threshold：

  选取阈值，形象来说就是在构造好的tree上横着切一刀，相连的叶结点属于同一个cluster；

  下图中，不同颜色的横线和叶结点上不同颜色的方框对应着切法与cluster的分法，比如按红色的线切就会分成2个cluster，按蓝色的线切就会分成3个cluster。

HAC和K-means最大的区别在于如何决定cluster的数量，在K-means里，K的值是要你直接决定的；而在HAC里，你并不需要直接决定分多少cluster，而是去决定“这一刀切在树的哪里”

3. Dimension Reduction

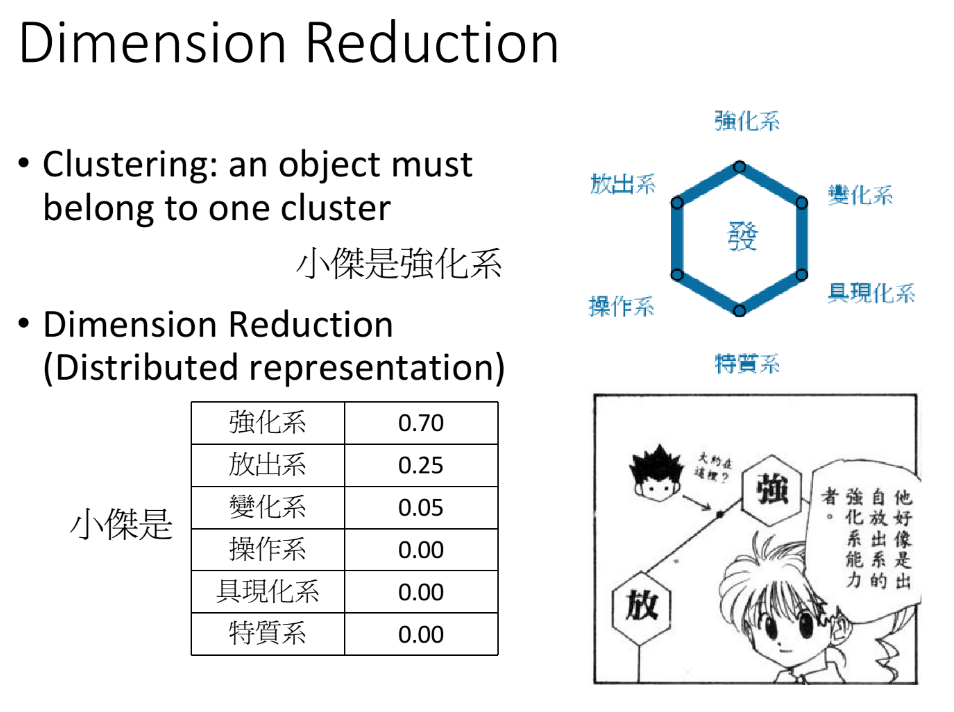
clustering的缺点是以偏概全，它强迫每个object都要属于某个cluster。但实际上某个object可能拥有多种属性，或者多个cluster的特征，如果把它强制归为某个cluster，就会失去很多信息；或许我们应该用一个vector来描述该object，这个vector的每一维都代表object的某种属性（这个vector的dimension肯定要比object原来的feature数目少），这种做法就叫做Distributed Representation。如果原先的object是high dimension的，比如image，那现在用计算出来的它的某些attribute（属性，特征）来描述它，就可以使之从高维空间转变为低维空间，这就是所谓的降维(Dimension Reduction)。Distribution Representation和Dimension Reduction其实是一样的事情，只是叫法不同。

比如哟下图中动漫“全职猎人”中小杰的念能力分布，从表中可以看出我们不能仅仅把他归为强化系，而应该要用一个vector来表示他的attribute。

3.1 Why Dimension Reduction Help?

接下来我们从另一个角度来看为什么Dimension Reduction可能是有用的。假设data为下图左侧中的3D螺旋式分布，你会发现用3D的空间来描述这些data其实是很浪费的，因为我们完全可以把这个卷摊平，此时只需要用2D的空间就可以描述这个3D的信息。

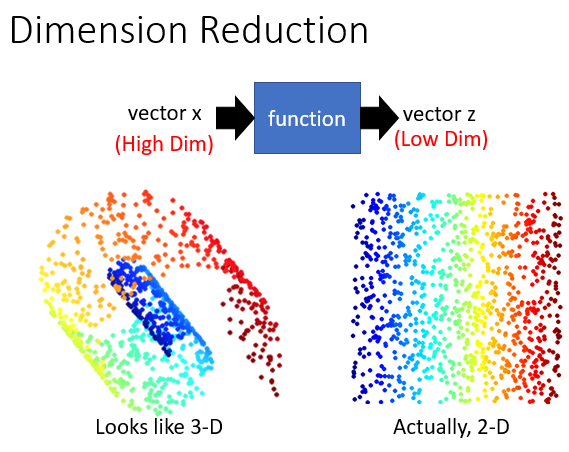
如果以MNIST(手写数字集)为例，每一张image都有28*28的dimension，但我们反过来想，大多数28*28 dimension的vector转成image，看起来都不会像是一个数字，所以描述数字所需要的dimension可能远比28*28要来得少。

举一个极端的例子，下面这几张表示“3”的image，我们完全可以用中间这张image旋转$\theta$角度来描述，也就是说，我们只需要用$\theta$这一个dimension就可以描述原先28*28 dimension的图像。你只要抓住角度的变化就可以知道28维空间中的变化，这里的28*28维pixel就是之前提到的樊一翁的胡子，而1维的角度则是他的头，也就是“去芜存菁，化繁为简”的思想

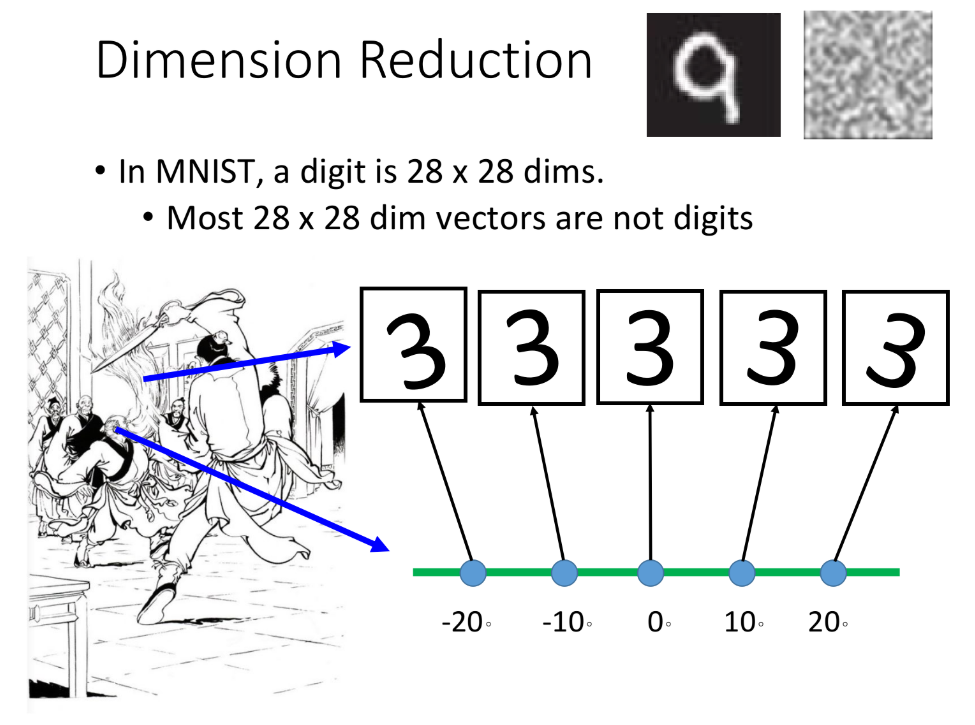
3.2. How to do Dimension Reduction？

那怎么去做Dimension Reduction呢，在Dimension Reduction里，我们要找一个function，这个function的input是原始的$x$，output是经过降维之后的$z$。最简单的方法是Feature Selection，即直接从原有的dimension里删掉一些直观上就对结果没有影响的dimension，就做到了降维，比如下图中从$x_1,x_2$两个维度中直接拿掉$x_1$；但这个方法不总是有用，因为很多情况下任何一个dimension其实都不能被拿掉，就像下图中的螺旋卷。

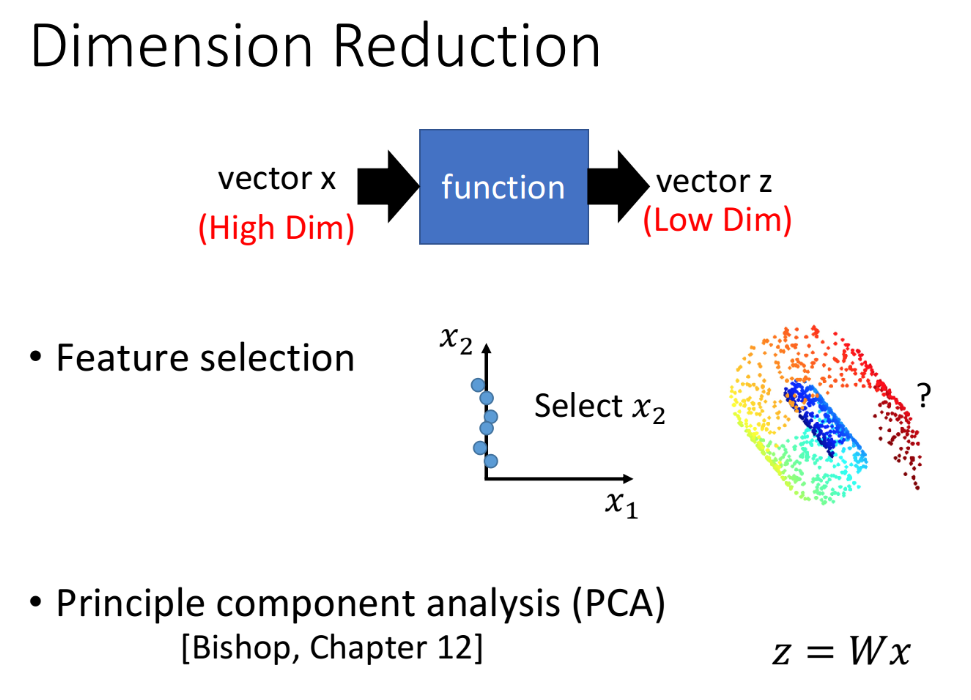
4. PCA

另一个常见的方法叫做PCA（Principe Component Analysis，主成分分析）。PCA认为降维就是一个很简单的linear function，它的input x和output z之间是linear transform，即$z=Wx$，PCA要做的，就是根据training data的$x$把W给找出来。

4.1 PCA for 1-Dimension

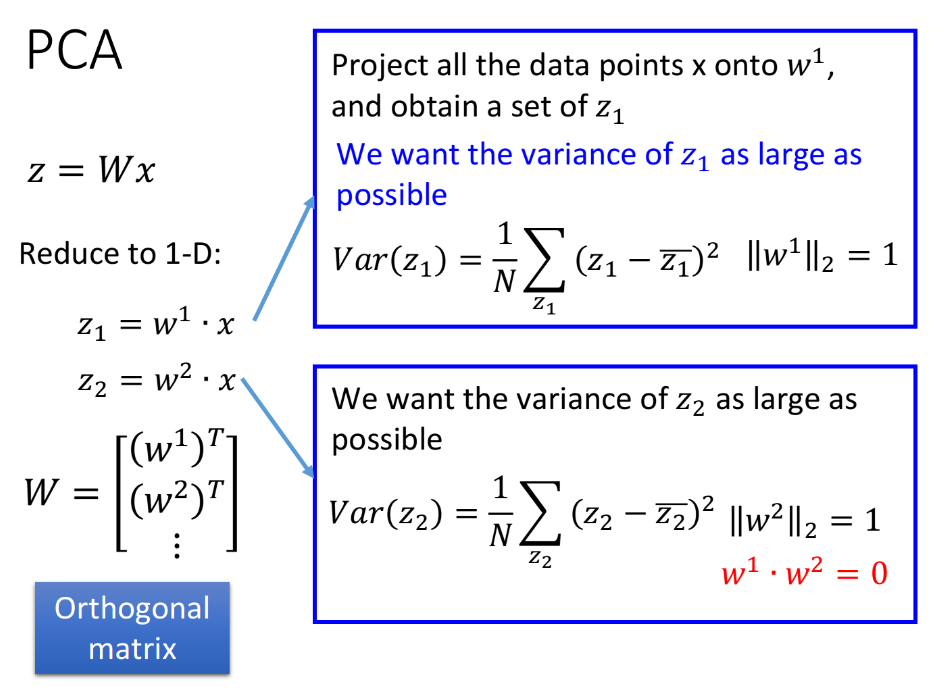
我们先考虑一个简单的case，假设$z$是1维的vector，也就是把$x$投影到一维空间，此时$W$是一个row vector。$z_1=w^1\cdot x$，其中$w^1$表示$w$的第一个row vector，我们假设$w^1$的长度为1，即$||w^1||_2=1$，此时$z_1$就是$x$在$w^1$方向上的投影。

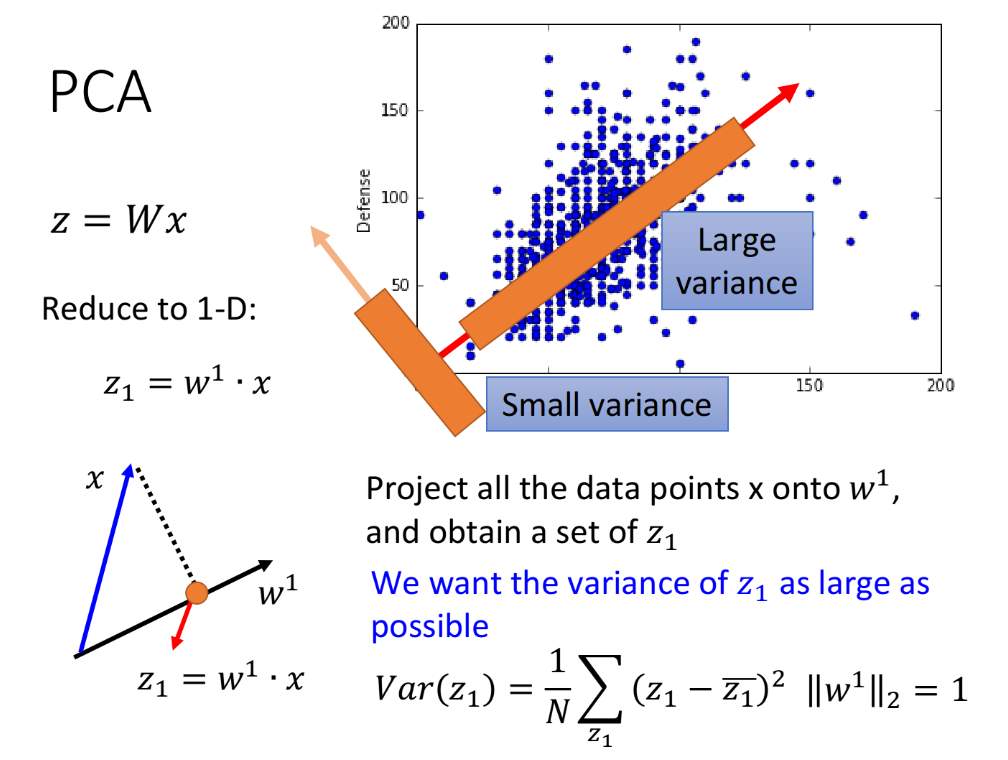
那我们到底要找什么样的$w^1$呢？假设我们现在已有的宝可梦样本点分布如下，横坐标代表宝可梦的攻击力，纵坐标代表防御力，我们的任务是把这个二维分布投影到一维空间上。我们希望选这样一个$w^1$，它使得$x$经过投影之后得到的$z_1$分布越大越好，也就是说经过这个投影后，不同样本点之间的区别，应该仍然是可以被看得出来的。即：

• 我们希望找一个projection（投影）的方向，它可以让$x$经过projection后的variance越大越好；

• 我们不希望projection使这些data point通通挤在一起，导致点与点之间的奇异度消失；

• 要去maximize的对象是$z_1$的variance，其中variance的计算公式：$Var(z_1)=\frac{1}{N}\sum\limits_{z_1}(z_1-\bar{z_1})^2, ||w^1||_2=1$，$\bar {z_1}$是$z_1$的平均值。

如下图给出了所有样本点在两个不同的方向上投影之后的variance比较情况，从这个图上，你可以看出$w^1$或许是代表宝可梦的强度，宝可梦可能有一个隐藏的factor代表它的强度，这个隐藏的factor同时影响了它的防御力跟攻击力，所以防御力跟攻击力是会同时上升的。

4.2 PCA for n-D

当然我们不可能只投影到一维空间，我们还可以投影到更高维的空间

对$z=Wx$来说：

• $z_1=w^1\cdot x$，表示$x$在$w^1$方向上的投影
• $z_2=w^2\cdot x$，表示$x$在$w^2$方向上的投影
• …

$z_1,z_2,…$串起来就得到$z$，而$w^1,w^2,…$分别是$W$的第1,2,…个row，需要注意的是，这里的$w^i$必须相互正交，此时$W$是正交矩阵(orthogonal matrix)，如果不加以约束，则算出来的的$w^1,w^2,…$实际上是相同的值 。

4.3. Lagrange multiplier

求解PCA，实际上已经有现成的函数可以调用，此外你也可以把PCA描述成neural network，然后用gradient descent的方法来求解，这里主要介绍用Lagrange multiplier（拉格朗日乘数法）求解PCA的数学推导过程。

（注：$w^i$和$x$均为列向量，下文中类似$w^i\cdot x$表示的是矢量内积，而$(w^i)^T\cdot x$表示的是矩阵相乘。）

Step1: calculate $w^1$

目标：maximize $(w^1)^TSw^1 $，条件：$(w^1)^Tw^1=1$

• 首先计算出$\bar{z_1}$：

  $$\begin{split} &z_1=w^1\cdot x\\ &\bar{z_1}=\frac{1}{N}\sum z_1=\frac{1}{N}\sum w^1\cdot x=w^1\cdot \frac{1}{N}\sum x=w^1\cdot \bar x \end{split}$$

• 然后计算maximize的对象$Var(z_1)$：

  （其中$Cov(x)=\frac{1}{N}\sum(x-\bar x)(x-\bar x)^T$）

  $$\begin{split} Var(z_1)&=\frac{1}{N}\sum\limits_{z_1} (z_1-\bar{z_1})^2\\ &=\frac{1}{N}\sum\limits_{x} (w^1\cdot x-w^1\cdot \bar x)^2\\ &=\frac{1}{N}\sum (w^1\cdot (x-\bar x))^2\\ &=\frac{1}{N}\sum(w^1)^T(x-\bar x)(x-\bar x)^T w^1\\ &=(w^1)^T\frac{1}{N}\sum(x-\bar x)(x-\bar x)^T w^1\\ &=(w^1)^T Cov(x)w^1 \end{split}$$

• 当然这里想要求$Var(z_1)=(w^1)^TCov(x)w^1$的最大值，还要加上$||w^1||_2=(w^1)^Tw^1=1$的约束条件，否则$w^1$可以取无穷大。

• 令$S=Cov(x)$，它是：

  • 对称的(symmetric)
  • 半正定的(positive-semidefine)，即所有特征值(eigenvalues)是非负的(non-negative)

  （看来是要复习一下研一上学的矩阵理论了(￣ω￣;)）

• 使用拉格朗日乘数法，利用目标和约束条件构造函数：

  $$g(w^1)=(w^1)^TSw^1-\alpha((w^1)^Tw^1-1)$$

• 对$w^1$这个vector里的每一个element做偏微分：

  $$\partial g(w^1)/\partial w_1^1=0\\ \partial g(w^1)/\partial w_2^1=0\\ \partial g(w^1)/\partial w_3^1=0\\ ...$$

• 整理上述推导式，可以得到：

  其中，$w^1$是$S$的特征向量(eigenvector)

  $$Sw^1=\alpha w^1$$

• 注意到满足$(w^1)^Tw^1=1$的特征向量$w^1$有很多，我们要找的是可以maximize $(w^1)^TSw^1$的那一个，于是利用上一个式子：

  $$(w^1)^TSw^1=(w^1)^T \alpha w^1=\alpha (w^1)^T w^1=\alpha$$

• 此时maximize $(w^1)^TSw^1$就变成了maximize $\alpha$，也就是$S$的最大的特征值$\alpha$对应的那个特征向量，就是我们要找的$w^1$

• 结论：$w^1$是$S=Cov(x)$这个matrix中的最大的特征值$\lambda_1$对应的特征向量

Step2: calculate $w^2$

在推导$w^2$时，相较于$w^1$，多了一个限制条件：$w^2$必须与$w^1$正交(orthogonal)。

目标：maximize $(w^2)^TSw^2$，条件：$(w^2)^Tw^2=1,(w^2)^Tw^1=0$

结论：$w^2$也是$S=Cov(x)$这个matrix第二大的特征值$\lambda_2$对应的特征向量

• 同样是用拉格朗日乘数法求解，先写一个关于$w^2$的function，包含要maximize的对象，以及两个约束条件

  $$g(w^2)=(w^2)^TSw^2-\alpha((w^2)^Tw^2-1)-\beta((w^2)^Tw^1-0)$$

• 对$w^2$的每个element做偏微分：

  $$\partial g(w^2)/\partial w_1^2=0\\ \partial g(w^2)/\partial w_2^2=0\\ \partial g(w^2)/\partial w_3^2=0\\ ...$$

• 整理后得到：

  $$Sw^2-\alpha w^2-\beta w^1=0$$

• 上式两侧同乘$(w^1)^T$，得到：

  $$(w^1)^TSw^2-\alpha (w^1)^Tw^2-\beta (w^1)^Tw^1=0$$

• 其中$\alpha (w^1)^Tw^2=0,\beta (w^1)^Tw^1=\beta$，

  而由于$(w^1)^TSw^2$是vector×matrix×vector=scalar，因此在外面套一个transpose（转置）不会改变其值，因此该部分可以转化为：

  （注：$S$是symmetric matrix（对称矩阵）的，既有$S^T=S$。）

  $$\begin{split} (w^1)^TSw^2&=((w^1)^TSw^2)^T\\ &=(w^2)^TS^Tw^1\\ &=(w^2)^TSw^1 \end{split}$$

  我们已经知道$w^1$满足$Sw^1=\lambda_1 w^1$，代入上式：

  $$\begin{split} (w^1)^TSw^2&=(w^2)^TSw^1\\ &=\lambda_1(w^2)^Tw^1\\ &=0 \end{split}$$

• 因此有$(w^1)^TSw^2=0$，$\alpha (w^1)^Tw^2=0$，$\beta (w^1)^Tw^1=\beta$，又根据

  $$(w^1)^TSw^2-\alpha (w^1)^Tw^2-\beta (w^1)^Tw^1=0$$

  可以推得$\beta=0$

• 此时$Sw^2-\alpha w^2-\beta w^1=0$就转变成了$Sw^2-\alpha w^2=0$，即

  $$Sw^2=\alpha w^2$$

• 由于$S$是symmetric的，因此在不与$w_1$冲突的情况下，这里$\alpha$选取第二大的特征值$\lambda_2$时，可以使$(w^2)^TSw^2$最大

• 结论：$w^2$也是$S=Cov(x)$这个matrix中的特征向量，对应第二大的特征值$\lambda_2$

（实对称矩阵的不同特征值对应的特征向量是正交的，这个在线性代数或者矩阵理论课程中都有讲过，或者可以参考實對稱矩陣可正交對角化的證明，这是我上学期末在复习矩阵理论的时候发现了一个台湾线代老师的博客，里面有非常多讲解线代知识的文章，思路和内容都要比SJTU用的教材好太多，简直救我期末于水火ヾ(ｏ･ω･)ﾉ）

4.4. PCA-decorrelation

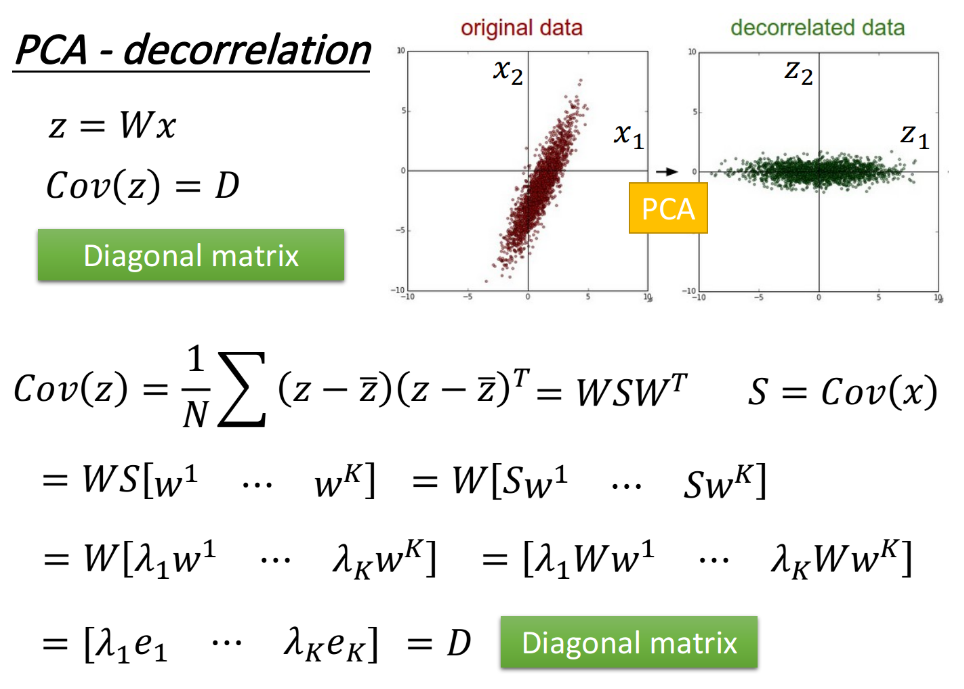
$z=W\cdot x$的神奇之处在于$Cov(z)=D$，即$z$的covariance是一个diagonal matrix，推导过程如下图所示。PCA可以让不同dimension之间的covariance变为0，即不同new feature之间是没有correlation的，这样做的好处是，减少feature之间的联系从而减少model所需的参数量。

如果你把原来的input data通过PCA之后再给其他model使用，那这些model就可以使用简单的形式，而无需考虑不同dimension之间类似$x_1\cdot x_2,x_3\cdot x_5^3,…$这些交叉项，此时model得到简化，参数量大大降低，相同的data量可以得到更好的训练结果，从而可以避免overfitting的发生。

5. PCA - Another Point of View

上面我们进行了PCA的数学推导，下面从另一个角度更直观地介绍PCA做了什么。

5.1. Reconstruction Component

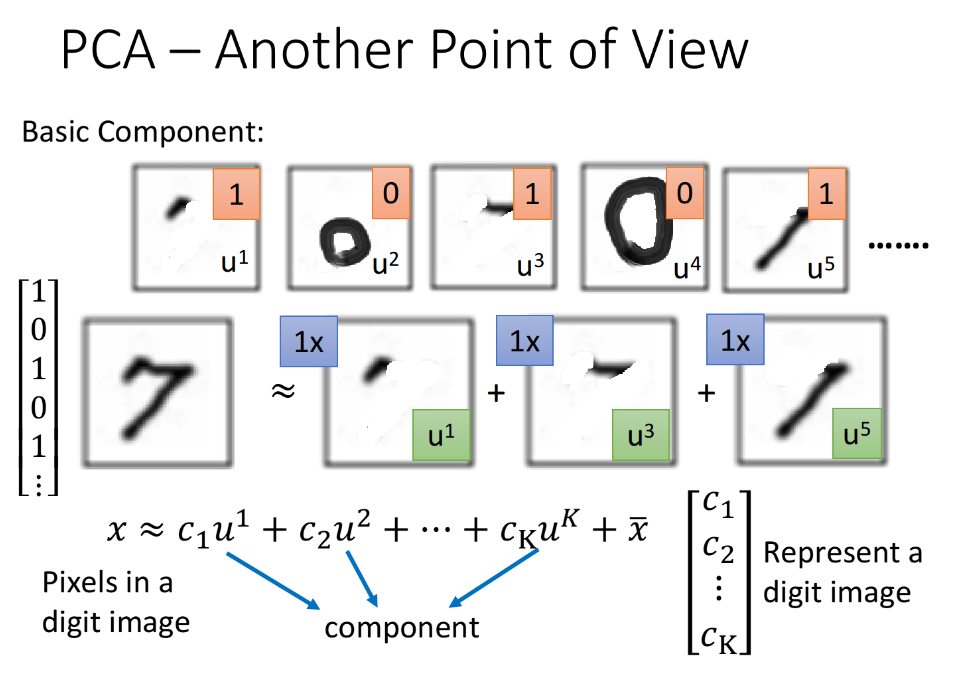
假设我们现在考虑的是手写数字识别，这些数字是由一些类似于笔画的basic component组成的，本质上就是一个vector，记做$u_1,u_2,u_3,…$，以MNIST为例，不同的笔画都是一个28×28的vector，把某几个vector加起来，就组成了一个28×28的digit，写成表达式就是：$x≈c_1u^1+c_2u^2+…+c_ku^k+\bar x$，其中$x$代表某张digit image中的pixel，它等于k个component的加权和$\sum c_iu^i$，加上所有image的平均值$\bar x$。

比如7就是$x=u^1+u^3+u^5$，我们可以用$\left [\begin{matrix}c_1\ c_2\ c_3…c_k \end{matrix} \right]^T$来表示一张digit image，如果component的数目k远比pixel的数目要小，那这个描述就是比较有效的。

实际上目前我们并不知道$u^1$~$u^k$具体的值，因此我们要找这样k个vector，使得$x-\bar x$与$\hat x$越接近越好：

$$x-\bar x≈c_1u^1+c_2u^2+...+c_ku^k=\hat x$$

而用未知component来描述的这部分内容，叫做Reconstruction error，即$||(x-\bar x)-\hat x||$，接下来我们就要去找k个vector $u^i$去minimize这个error：

$$L=\min\limits_{u^1,...,u^k}\sum||(x-\bar x)-(\sum\limits_{i=1}^k c_i u^i) ||_2$$

回顾PCA，$z=W\cdot x$，实际上我们通过PCA最终解得的$\{w^1,w^2,…,w^k\}$就是使reconstruction error最小化的$\{u^1,u^2,…,u^k\}$，简单证明如下：

• 将所有的$x^i-\bar x≈c_1^i u^1+c_2^i u^2+…$写在一起，就可以用下图中的矩阵相乘来表示，我们的目标是使等号两侧矩阵之间的差距越小越好；

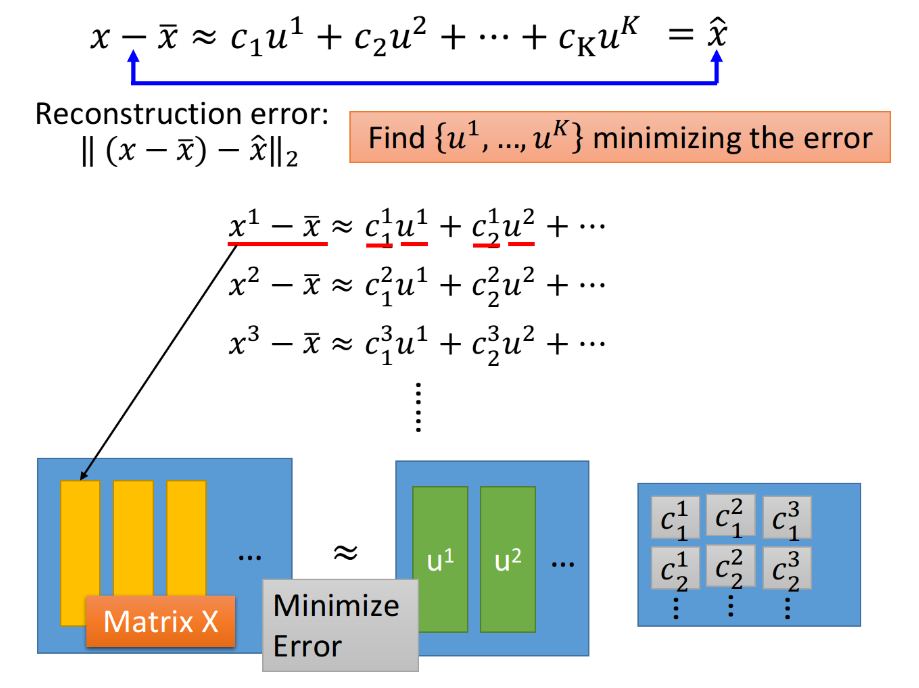
• 可以使用SVD（Singular Value Decomposition，奇异值分解）将每个matrix $X_{m×n}$都拆成matrix $U_{m×k}$、$\Sigma_{k×k}$、$V_{k×n}$的乘积，其中k为component的数目；

  （SVD可以参考奇異值分解專題)，我之前也有纸质笔记，有时间的话可以整理一下，咕咕咕。）

• 值得注意的是，使用SVD拆解后的三个矩阵相乘，是跟等号左边的矩阵$X$最接近的，此时$U$就对应着$u^i$那部分的矩阵，$\Sigma\cdot V$就对应着$c_k^i$那部分的矩阵

• 根据SVD的结论，组成矩阵$U$的k个列向量(标准正交向量, orthonormal vector)就是$XX^T$最大的k个特征值(eignvalue)所对应的特征向量(eigenvector)，而$XX^T$实际上就是$x$的covariance matrix，因此$U$就是PCA的k个解组成的matrix；

• 因此我们可以发现，通过PCA找出来的Dimension Reduction的transform，实际上就是把$X$拆解成能够最小化Reconstruction error的component的过程，通过PCA所得到的$w^i$就是component $u^i$，而Dimension Reduction的结果就是参数$c_i$

• 简单来说就是，用PCA对$x$进行降维的过程中，我们要找的投影方式$w^i$就相当于恰当的组件$u^i$，投影结果$z^i$就相当于这些组件各自所占的比例$c_i$

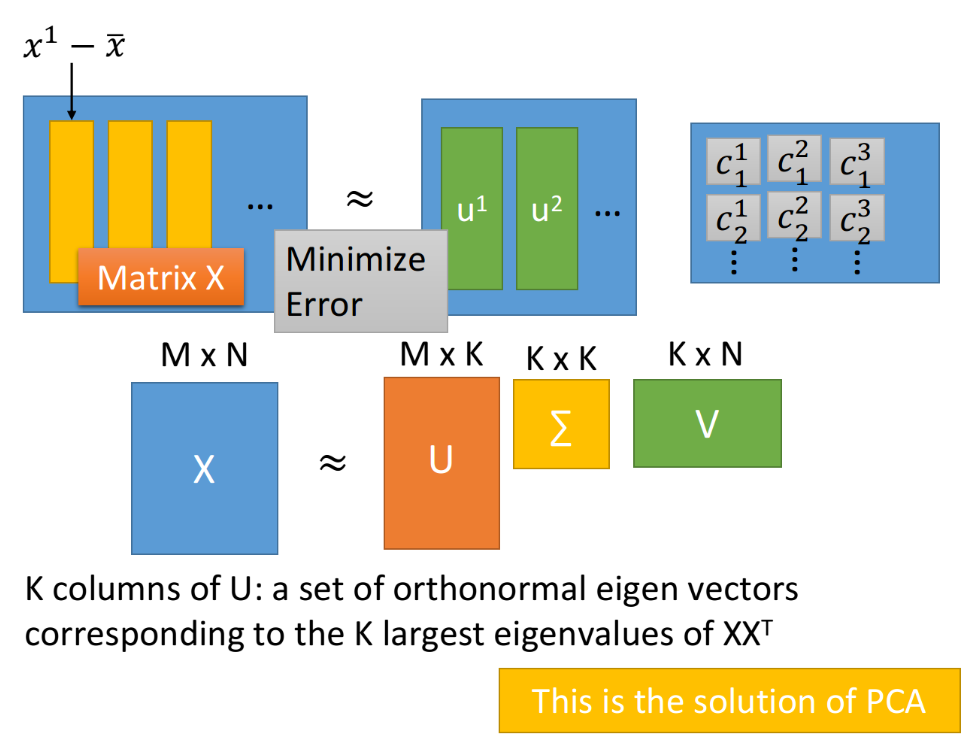
• 下面的式子简单演示了将一个样本点$x$划分为k个组件的过程，其中$\left [\begin{matrix}c_1 \ c_2\ … c_k \end{matrix} \right ]^T$是每个组件的比例；把$x$划分为k个组件即从n维投影到k维空间，$\left [\begin{matrix}c_1 \ c_2\ … c_k \end{matrix} \right ]^T$也是投影结果，其中$x$和$u_i$均为n维列向量。

  $$\begin{split} &x= \left [ \begin{matrix} u_1\ u_2\ ...\ u_k \end{matrix} \right ]\cdot \left [ \begin{matrix} c_1\\ c_2\\ ...\\ c_k \end{matrix} \right ]\\ \\ &\left [ \begin{matrix} x_1\\ x_2\\ ...\\ x_n \end{matrix} \right ]=\left [ \begin{matrix} u_1^1\ u_2^1\ ... u_k^1 \\ u_1^2\ u_2^2\ ... u_k^2 \\ ...\\ u_1^n\ u_2^n\ ... u_k^n \end{matrix} \right ]\cdot \left [ \begin{matrix} c_1\\ c_2\\ ...\\ c_k \end{matrix} \right ]\\ \end{split}$$

5.2. NN for PCA

现在我们已经知道，用PCA找出来的$\{w^1,w^2,…,w^k\}$就是k个component $\{u^1,u^2,…,u^k\}$，而$\hat x=\sum\limits_{k=1}^K c_k w^k$，我们要使$\hat x$与$x-\bar x$之间的差距越小越好，我们已经根据SVD找到了$w^k$的值，而对每个不同的样本点，都会有一组不同的$c_k$值，在PCA中我们已经证得，$\{w^1,w^2,…,w^k\}$这k个vector是标准正交化的(orthonormal)，因此：

$$c_k=(x-\bar x)\cdot w^k$$

这个时候我们就可以使用神经网络来表示整个过程，假设$x$是3维向量，要投影到k=2维的component上：

• 对$x-\bar x$与$w^k$做inner product的过程类似于neural network，$x-\bar x$在3维空间上的坐标就相当于是neuron的input，而$w^1_1$，$w^1_2$，$w^1_3$则是neuron的weight，表示在$w^1$这个维度上投影的参数，而$c_1$则是这个neuron的output，表示在$w^1$这个维度上投影的坐标值；对$c_2$也同理

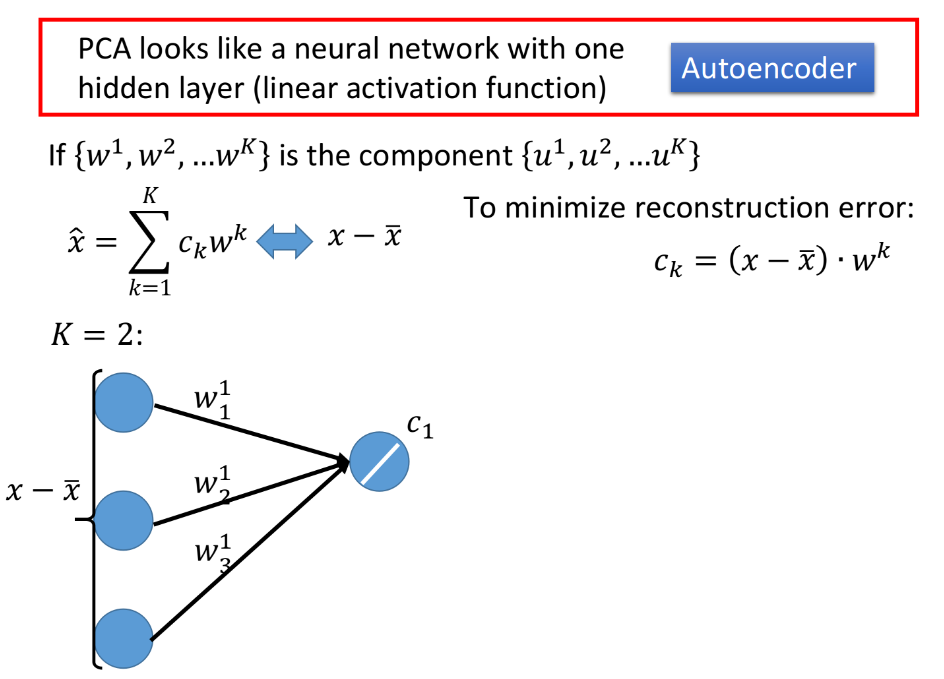
• 得到$c_1$之后，再让它乘上$w^1$，得到$\hat x$的一部分

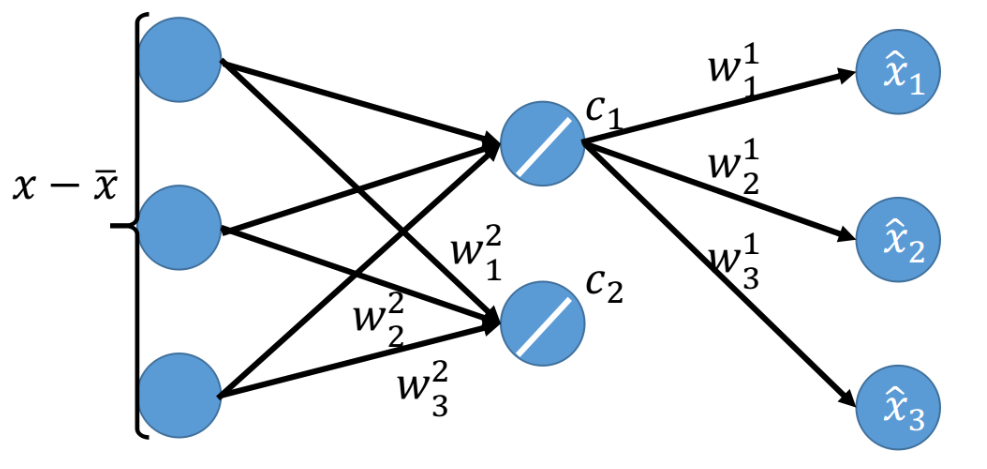
• 对$c_2$进行同样的操作，乘上$w^2$，贡献$\hat x$的剩余部分，此时我们已经完整计算出$\hat x$三个分量的值

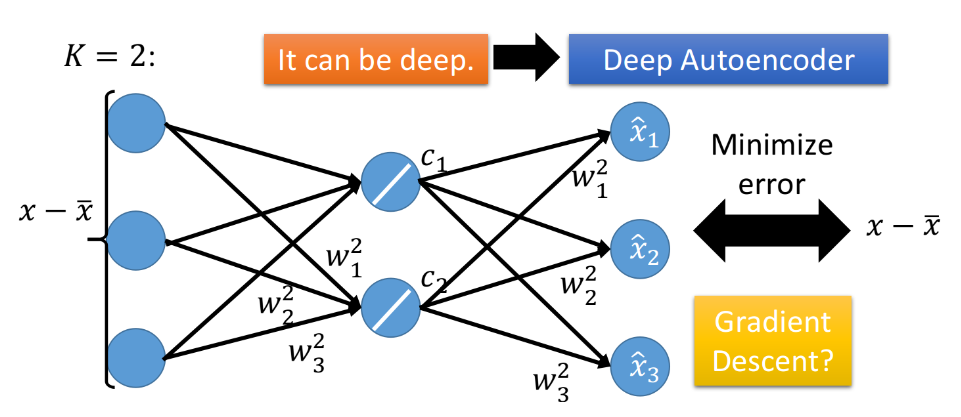
• 此时，PCA就被表示成了只含一层hidden layer的神经网络，且这个hidden layer是线性的激活函数，训练目标是让这个NN的input $x-\bar x$与output $\hat x$越接近越好，这件事就叫做Autoencoder。

• 注意，通过PCA求解出的$w^i$与直接对上述的神经网络做梯度下降所解得的$w^i$是会不一样的，因为PCA解出的$w^i$是正交的(orgonormal)，而用NN的方式得到的解无法保证$w^i$相互垂直，NN无法做到Reconstruction error比PCA小，因此：

  • 在linear的情况下，直接用PCA找$W$远比用神经网络的方式更快速方便
  • 用NN的好处是，它可以使用不止一层hidden layer，它可以做deep autoencoder

5.3. Weakness of PCA

PCA也有很明显的弱点：

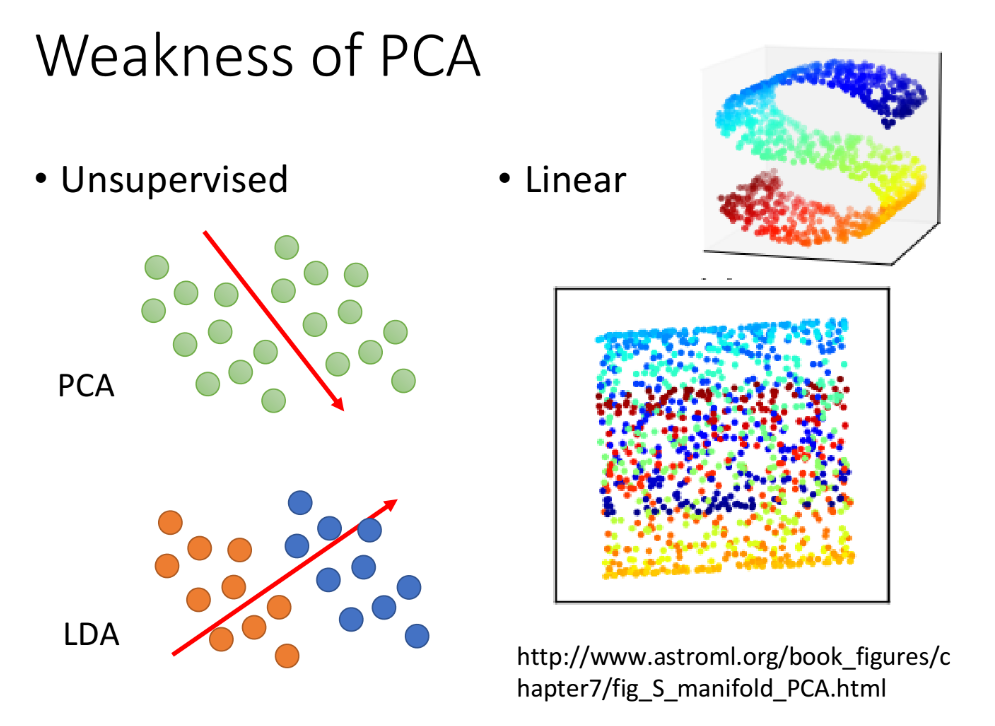
• 它是unsupervised的，如果我们要将下图绿色的点投影到一维空间上，PCA给出的从左上到右下的划分很有可能使原本属于蓝色和橙色的两个class的点被merge在一起

  这时要解决问题可能就需要引入label data，LDA（Linear Discriminant Analysis，线性判别分析）则是考虑了labeled data之后进行降维的一种方式，但属于supervised，不在本文讨论。

LDA不同于PCA方差最大化理论，LDA算法的思想是将数据投影到低维空间之后，使得同一类数据尽可能的紧凑，不同类的数据尽可能分散。因此，LDA算法是一种有监督的机器学习算法。同时，LDA有如下两个假设:(1) 原始数据根据样本均值进行分类。(2) 不同类的数据拥有相同的协方差矩阵。

（摘自文章机器学习-LDA(线性判别降维算法)）

• 它是linear的，对于下图中的彩色曲面，我们期望把它平铺拉直进行降维，但这是一个non-linear的投影转换，PCA无法做到这件事情，PCA只能做到把这个曲面打扁压在平面上，类似下图，而无法把它拉开。对类似曲面空间的降维投影，需要用到non-linear transformation

6. More Examples

6.1. PCA for Pokemon

这里举一个实际应用的例子，用PCA来分析宝可梦的数据，假设总共有800只宝可梦，每只都用一个六维的vector来表示，即vector={HP, Atk, Def, Sp Atk, Sp Def, Speed}，然后我们用PCA来分析，首先要面对的问题是，要将6维的vector投影到多少维的空间上？

如果做可视化分析的话，投影到二维或三维平面可以方便人眼观察，实际上，宝可梦的$cov(x)$是6维，最多可以投影到6维空间。一个常用的方法是：我们可以先找出6个特征向量和对应的特征值$\lambda_i$，其中$\lambda_i$表示第$i$个投影维度的variance有多大(即在第i个维度的投影上点的散步程度有多大，variance越大，点的分布就越散，这也是我们所希望的)，然后我们就可以计算出每个$\lambda_i$的比例，ratio=$\frac{\lambda_i}{\sum\limits_{i=1}^6 \lambda_i}$

从上图的ratio可以看出$\lambda_5$、$\lambda_6$所占比例不高，即第5和第6个principle component(可以理解为维度)所发挥的作用是比较小的，用这两个dimension做投影所得到的variance很小，投影在这两个方向上的点比较集中，意味着这两个维度表示的是宝可梦的共性，无法对区分宝可梦的特性做出太大的贡献，所以我们只需要利用前4个principle component即可。

注意到新的维度本质上就是旧的维度的加权矢量和，下图给出了前4个维度的加权情况，从PC1到PC4这4个principle component都是6维度加权的vector，它们都可以被认为是某种组件，每一个宝可梦都可以由这4个principle component加权之和。

我们来仔细分析一下这四个component代表的“含义”：

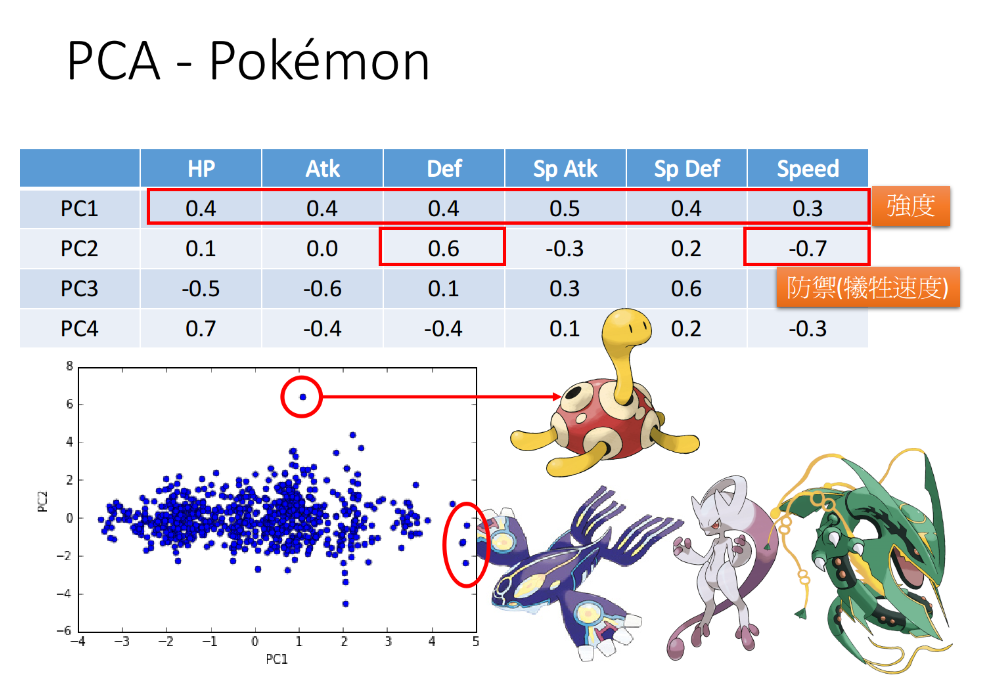
• 对第一个vector PC1来说，每个值都是正的，因此这个组件在某种程度上代表了宝可梦的强度

• 对第二个vector PC2来说，防御力Def很大而速度Speed很小，这个组件可以增加宝可梦的防御力但同时会牺牲一部分的速度

• 如果将宝可梦仅仅投影到PC1和PC2这两个维度上，则降维后的二维可视化图像如下图所示：

  从该图中也可以得到一些信息：

  • 在PC2维度上特别大的那个样本点刚好对应着普普(海龟)，确实是防御力且速度慢的宝可梦
  • 在PC1维度上特别大的那三个样本点则对应着盖欧卡、超梦等综合实力很强的宝可梦

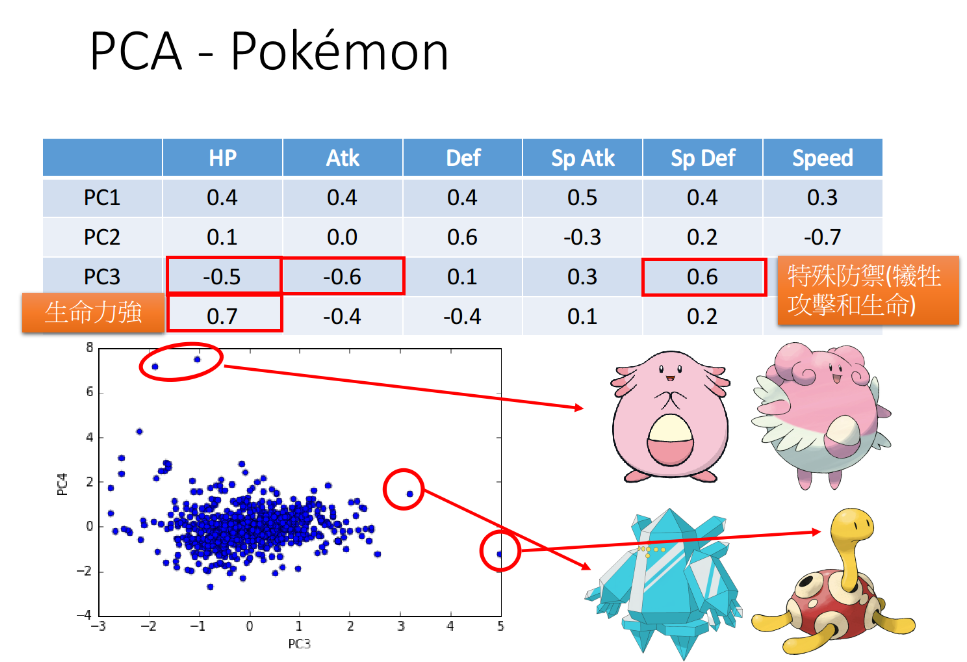
• 对第三个vector PC3来说，sp Def很大而HP和Atk很小，这个组件是用生命力和攻击力来换取特殊防御力

• 对第四个vector PC4来说，HP很大而Atk和Def很小，这个组件是用攻击力和防御力来换取生命力

• 同样将宝可梦只投影到PC3和PC4这两个维度上，则降维后得到的可视化图像如下图所示：

  该图同样可以告诉我们一些信息：

  • 在PC3维度上特别大的样本点依旧是普普，第二名是冰柱机器人，它们的特殊防御力都比较高
  • 在PC4维度上特别大的样本点则是吉利蛋和幸福蛋，它们的生命力比较强

6.2. PCA for MNIST

再次回到手写数字识别的问题上来，这个时候我们就可以熟练地把一张数字图像用多个组件(维度)表示出来了：

$$digit\ image=a_1 w^1+a_2 w^2+...$$

这里的$w^i$就表示降维后的其中一个维度，即一个principle component，它是由原先28×28维进行加权求和的结果，因此$w^i$也是一张28×28的图像，下图列出了通过PCA得到的前30个组件的形状：

注：PCA就是求$Cov(x)=\frac{1}{N}\sum (x-\bar x)(x-\bar x)^T$的前30个最大的特征值对应的特征向量

6.3. PCA for Face Recognition

同理，在人脸识别的例子中，通过PCA找出人脸的前30个component(维度)，如下图所示，用这些脸的组件做线性组合就可以得到所有的脸。

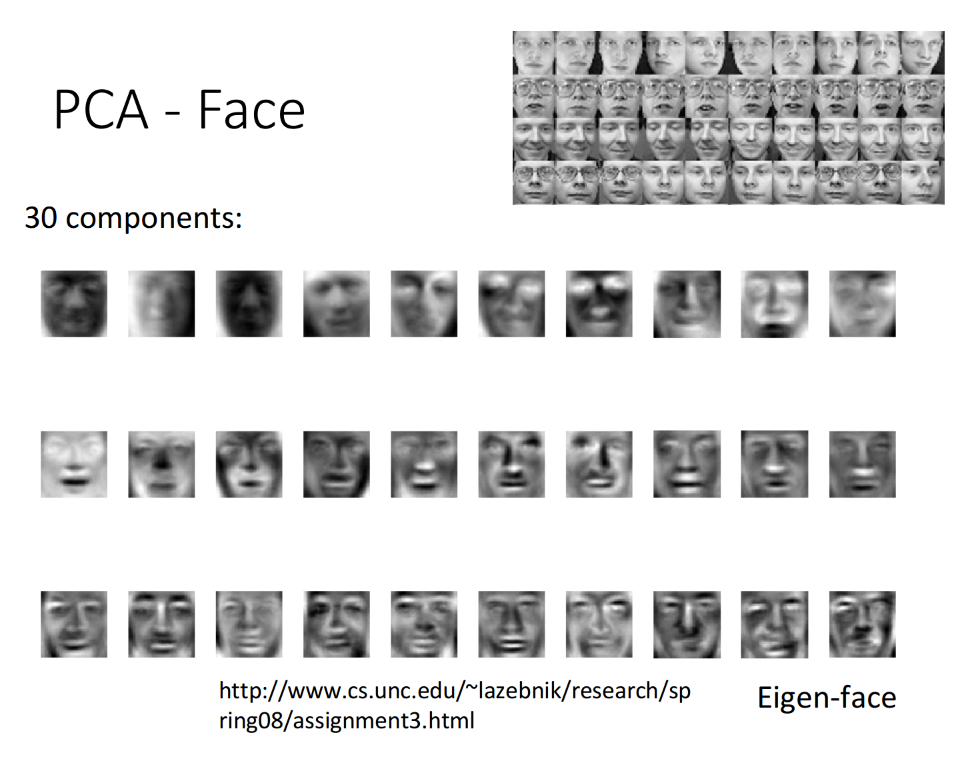
在对MNIST和Face的PCA结果展示的时候，你可能会注意到我们找到的组件好像并不算是组件，比如MNIST找到的几乎是完整的数字雏形，而Face找到的也几乎是完整的人脸雏形，但我们预期的组件不应该是类似于横折撇捺，眼睛鼻子眉毛这些吗？如果你仔细思考了PCA的特性，就会发现得到这个结果是可能的：

$$digit\ image=a_1 w^1+a_2 w^2+...$$

注意到linear combination的weight $a_i$可以是正的也可以是负的，因此我们可以通过把组件进行相加或相减来获得目标图像，这会导致你找出来的component不是基础的组件，但是通过这些组件的加加减减肯定可以获得基础的组件元素。

6.4. NMF

如果你要一开始就得到类似笔画这样的基础组件，就要使用NMF(non-negative matrix factorization)，非负矩阵分解的方法。PCA可以看成对原始矩阵$X$做SVD进行矩阵分解，但并不保证分解后矩阵的正负，实际上当进行图像处理时，如果部分组件的matrix包含一些负值的话，如何处理负的像素值也会成为一个问题(可以做归一化处理，但比较麻烦)。而NMF的基本思想是，强迫使所有component的每一个dimension都是正的，且它的加权值$a_1$都必须是正的，也就是说所有图像都必须由组件叠加得到：

• Forcing $a_1$, $a_2$…… be non-negative
  • additive combination
• Forcing $w_1$, $w_2$…… be non-negative
  • More like “parts of digits”

(注：关于NMF的具体算法内容可参考paper Daniel D. Lee and H. Sebastian Seung. “Algorithms for non-negative matrix factorization.”Advances in neural information processing systems. 2001. ）

NMF for MNIST

在MNIST数据集上，通过NMF找到的前30个组件如下图所示，可以发现这些组件都是由基础的笔画构成：

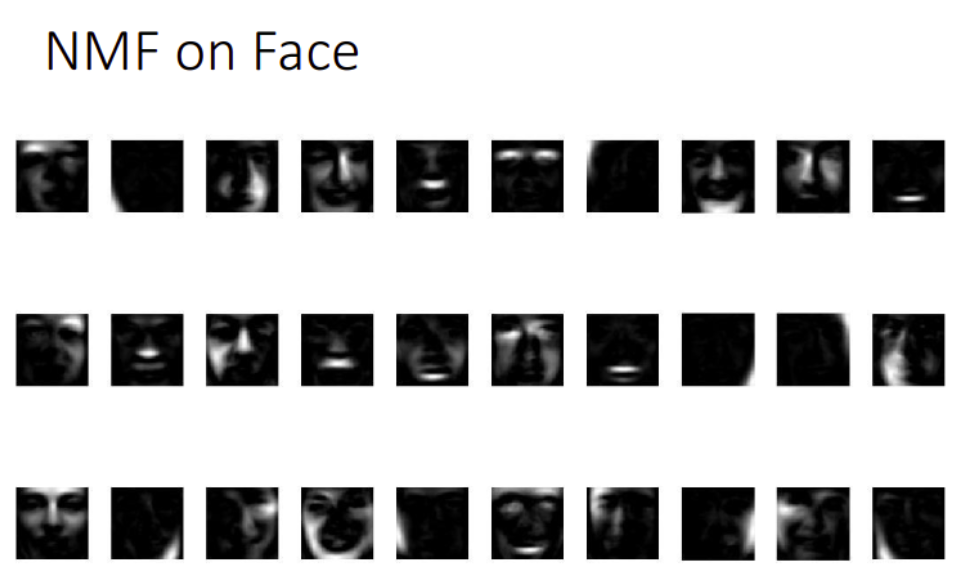
NMF for Face

在Face数据集上，通过NMF找到的前30个组价如下图所示，相比于PCA这里更像是脸的一部分

More Related Approaches

降维的方法有很多，这里再列举一些与PCA有关的方法：

• Multidimensional Scaling (MDS) [Alpaydin, Chapter 6.7]

  MDS不需要把每个data都表示成feature vector，只需要知道特征向量之间的distance，就可以做降维，PCA保留了原来在高维空间中的距离，在某种情况下MDS就是特殊的PCA

• Probabilistic PCA [Bishop, Chapter 12.2]

  PCA概率版本

• Kernel PCA [Bishop, Chapter 12.3]

  PCA非线性版本

• Canonical Correlation Analysis (CCA) [Alpaydin, Chapter 6.9]

  CCA常用于两种不同的data source的情况，比如同时对声音信号和唇形的图像进行降维

• Independent Component Analysis (ICA)

  ICA常用于source separation，PCA找的是正交的组件，而ICA则只需要找“独立”的组件即可

• Linear Discriminant Analysis (LDA) [Alpaydin, Chapter 6.8]

  LDA是supervised的方式

7. Matrxi Factorization

接下来用一个简单的推荐系统的例子来介绍下矩阵分解的思想。有时候存在两种object，它们之间会受到某种共同潜在因素(latent factor)的操控，如果我们找出这些潜在因素，就可以对用户的行为进行预测，这也是推荐系统常用的方法之一。

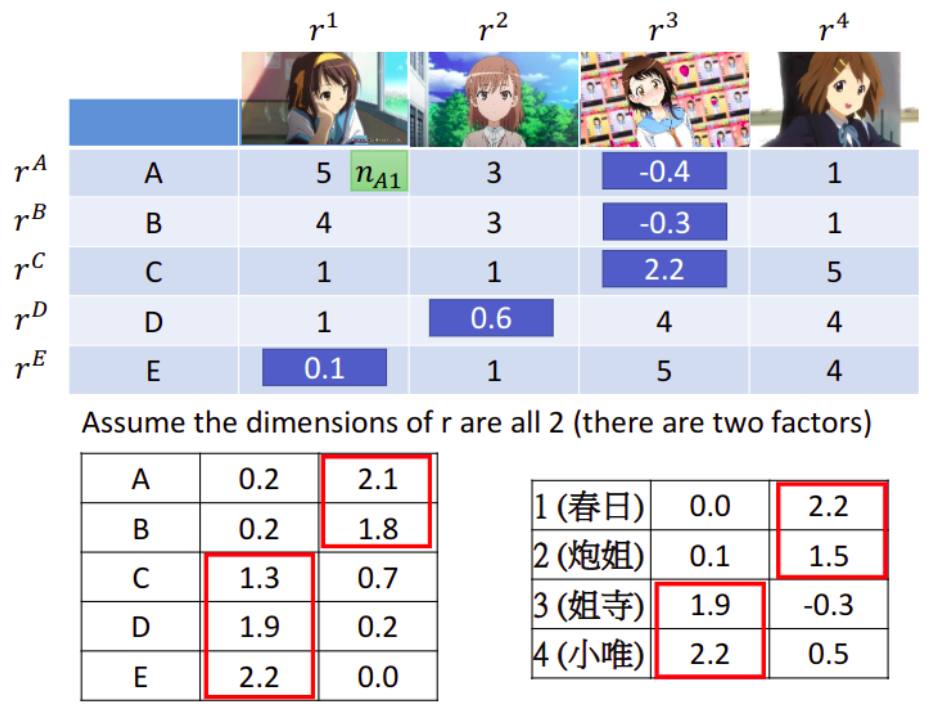
假设我们现在去调查每个人购买的手办数目，ABCDE代表5个人，每个人或者每个手办的动漫人物实际上都是有着傲娇的属性或天然呆的属性（老师是老二次元实锤）。我们可以用vector去描述人和公仔的属性，如果某个人的属性和某个公仔的属性是match的，即他们背后的vector很像(内积值很大)，这个人就会偏向于拥有更多这种类型的公仔。

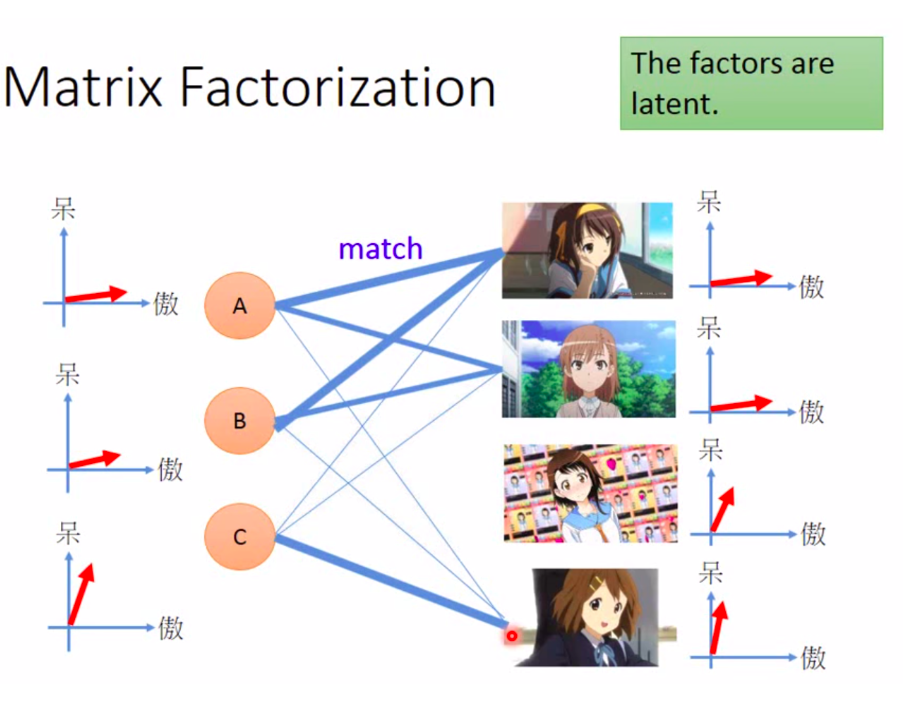
matrix expression

但是，我们没有办法直接观察某个人背后这些潜在的属性，也不会有人在意一个肥宅心里想的是什么（肥宅大哭），我们同样也没有办法直接得到动漫人物背后的属性；我们目前有的，只是动漫人物和人之间的关系，即每个人已购买的公仔数目，我们要通过这个关系去推测出动漫人物与人背后的潜在因素(latent factor)。

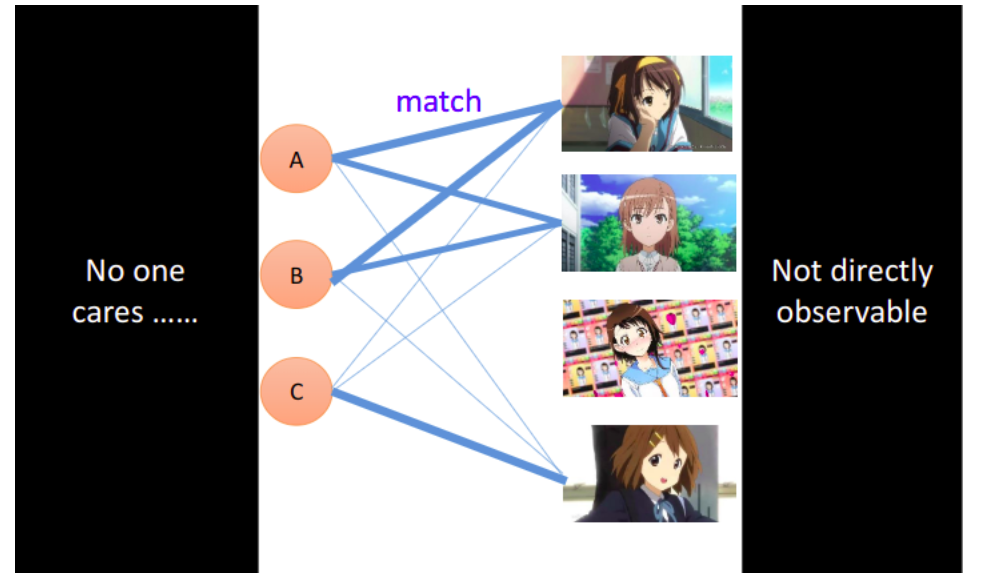
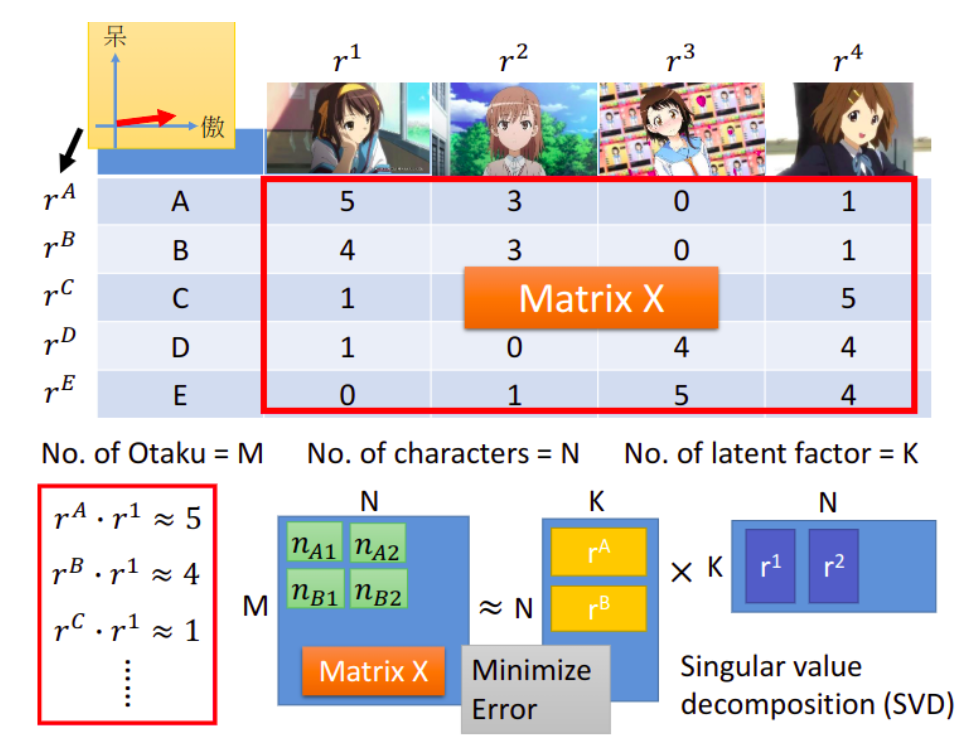
我们可以把每个人的属性用vector $r^A$、$r^B$、$r^C$、$r^D$、$r^E$来表示，而动漫人物的属性则用vector $r^1$、$r^2$、$r^3$、$r^4$来表示，购买的公仔数目可以被看成是matrix $X$，对$X$来说，行数为人数，列数为动漫角色的数目。做一个假设：matrix $X$里的每个element，都是属于人的vector和属于动漫角色的vector的内积，比如，$r^A\cdot r^1≈5$，表示$r^A$和$r^1$的属性比较贴近，那A这个人就会买比较多凉宫春日的手办。

接下来就用下图所示的矩阵相乘的方式来表示这样的关系，其中$K$为latent factor的数量，这是未知的，需要你自己去调整选择，我们要找一组$r^A$~$r^E$和$r^1$~$r^4$，使得右侧两个矩阵相乘的结果与左侧的matrix $X$越接近越好，可以使用SVD的方法求解。

prediction

但有时候，部分的information可能是会missing的，这时候就难以用SVD精确描述，但我们可以使用梯度下降的方法求解，loss function如下：

$$L=\sum\limits_{(i,j)}(r^i\cdot r^j-n_{ij})^2$$

其中$r^i$值的是人背后的latent factor，$r^j$指的是动漫角色背后的latent factor，我们要让这两个vector的内积与实际购买该公仔的数量$n_{ij}$越接近越好，这个方法的关键之处在于，计算上式时，可以跳过missing的数据，最终通过gradient descent求得$r^i$和$r^j$的值。

假设latent factor的数目等于2，则人的属性$r^i$和动漫角色的属性$r^j$都是2维的vector，这里实际进行计算后，把属性中较大值标注出来，可以发现：

• 人：A、B属于同一组属性，C、D、E属于同一组属性

• 动漫角色：1、2属于同一组属性，3、4属于同一组属性

• 结合动漫角色，可以分析出动漫角色的第一个维度是天然呆属性，第二个维度是傲娇属性

• 接下来就可以预测未知的值，只需要将人和动漫角色的vector做内积即可

这样就可以针对阿宅做一个简单的推荐系统了。

more about matrix factorization

实际上除了人和动漫角色的属性之外，可能还存在其他因素操控购买数量这一数值，因此我们可以将式子更精确地改写为：

$$r^A\cdot r^1+b_A+b_1≈5$$

其中$b_A$表示A这个人本身有多喜欢买公仔，$b_1$则表示这个动漫角色本身有多受欢迎，这些内容是跟属性vector无关的，此时loss function被改写为：

$$L=\sum\limits_{(i,j)}(r^i\cdot r^j+b_i+b_j-n_{ij})^2$$

当然你也可以加上一些regularization去对结果做约束。（有关Matrix Factorization和推荐系统更多内容的介绍，可以参考paper Matrix Factorization Techniques For Recommender Systems；有关Matrix Factorization的理论知识，可以参考：線代啟示錄）

for Topic Analysis

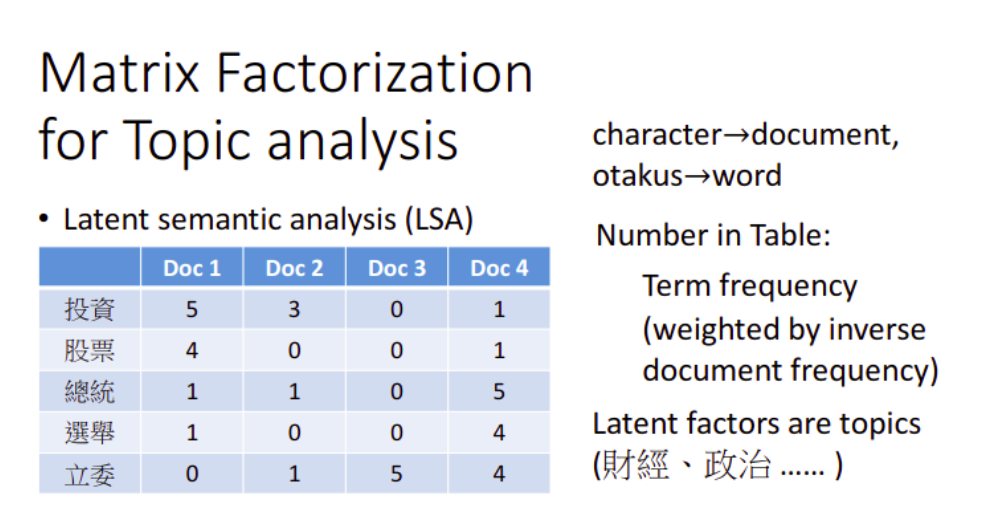
如果把matrix factorization的方法用在topic analysis上，就叫做LSA(Latent semantic analysis)，潜在语义分析。我们只需要把动漫人物换成文章，人换成词汇，表中的值从购买数量换成词频即可，table里面的值就是term frequency，把这个term frequency乘上一个weight代表说这个term本身有多重要。

Evaluation一个term的重要性的常用的方式是：inverse document frequency(计算每一个词汇在整个paper有多少比率的document涵盖这个词汇，假如说，每个词汇，每个document都有，那它的inverse document frequency就很小，代表着这个词汇的重要性是低的，假设某个词汇只有某一篇document有，那它的inverse document frequency就很大，代表这个词汇对于这篇文章的重要性是高的，这个词汇的含义与文章的语义关联性就比较高。)

在这个task里，做matrix factorization，就会找到每一个document背后的latent factor，它可能指的是topic(主题)，这个topic有多少是跟财经有关的，有多少是跟政治有关的。document1跟document2有比较多的“投资，股票”这样的词汇，那document1跟document2就有比较高的可能背后的latent factor是比较偏向“财经”的。我们可以用词汇的重要性给词频加权，在各种文章中出现次数越多的词汇越不重要，出现次数越少则越重要。这个场景下找出的latent factor可能会是主题(topic)，比如某个词汇或某个文档有多少比例是偏向于财经主题、政治主题…

Topic analysis的方法多如牛毛，但基本的思想是差不多的，常见的方法有pLSA（probability latent semantic analysis，概率潜在语义分析）和LDA（latent Dirchlet allocation，隐含狄利克雷分布）。注意这里的LDA和之前在5.3节提到的LDA是不一样的。

pLSA 可以参考：pLSA原理及其代码实现；

LDA 可以参考：一文详解LDA主题模型