贷款违约预测（1）赛题理解

1.赛题概况

比赛地址：零基础入门金融风控-贷款违约预测

本次比赛以金融风控中的个人信贷为背景，根据贷款申请人的数据信息预测其是否有违约的可能，以此判断是否通过此项贷款，是一个二分类问题。

赛题的数据来自某信贷平台的贷款记录，包括47列变量信息，其中15列为匿名变量，比赛界面有对应的数据概况介绍，说明列的性质特征。总数据量120万条，其中，训练集80万条，测试集A 20万条，测试集B 20万条。

预测指标：采用AUC作为评价指标，AUC越接近1.0，模型的预测性能越好。

2.二分类问题中常见的评估指标

1.混淆矩阵（Confuse Matrix）

二分类问题的预测结果可以根据情况分成以下四类：

（1）真正 TP（True Positive）：预测值为1，真实值为1

（2）假正 FP（False Positive）：预测值为1，真实值为0

（3）真负 TN（True Negative）：预测值为1，真实值为0

（4）假负 FN（False Negative）：预测值为0，真实值为1

import numpy as np
from sklearn.metrics import confusion_matrix
y_true = [0, 1, 0, 1]
y_pred = [1, 1, 1, 0]
confusion_matrix(y_true, y_pred)

1 2	array([[0, 2], [1, 1]], dtype=int64)

1 2	tn, fp, fn, tp = confusion_matrix([0, 1, 0, 1], [1, 1, 1, 0]).ravel() (tn, fp, fn, tp)

1	(0, 2, 1, 1)

2.准确率（Accuracy）

分类正确的样本数占总样本数的比例数。准确率在样本不均衡的数据集上不适用。

$Accuracy = \frac{TP+TN}{TP+TN+FP+FN}$

3.精确率（Precision）

又称查准率，正确预测为正样本（TP）占预测为正样本（TP+FP）的比例。

$Percision=\frac{TP}{TP+FP}$

4.召回率（Recall）

又称查全率，正确预测为正样本（TP）占正样本的（TP+FN）比例。

$Recall=\frac{TP}{TP+FN}$

5.F1 - score

Precision和Recall指标有时是此消彼长的，即精准率高了，召回率就下降，在一些场景下要兼顾精准率和召回率，最常见的方法就是F-Measure，又称F-Score。F-Measure是P和R的加权调和平均，即；

$\frac{1}{F_{\beta}}=\frac{1}{1+\beta^2} \cdot \left( \frac{1}{P}+\frac{\beta^2}{R}\right) \\ F_{\beta} = \frac{(1+\beta^2)\times P \times R}{(\beta^2 \times P) + R}$

当$\beta=1$时，也就是常见的F1-Score，是P和R的调和平均，当F1较高时，模型的性能越好。

$F1-Socre = \frac{2\times P \times R }{P+R}$

from sklearn import metrics

y_true = [0, 1, 0, 1]
y_pred = [1, 1, 1, 0]

print('accuracy:',  metrics.accuracy_score(y_true, y_pred))
print('precision:', metrics.precision_score(y_true, y_pred))
print('recall:', metrics.recall_score(y_true, y_pred))
print('f1-score:', metrics.f1_score(y_true, y_pred))

accuracy: 0.25
precision: 0.3333333333333333
recall: 0.5
f1-score: 0.4

6.P-R曲线（Precision-Recall Curve）

描述精确率/召回率变化的曲线。

若一个学习器A的P-R曲线被另一个学习器B的P-R曲线完全包住，则称：B的性能优于A。若A和B的曲线发生了交叉，则谁的曲线下的面积大，谁的性能更优。但一般来说，曲线下的面积是很难进行估算的，所以衍生出了“平衡点”（Break-Event Point，简称BEP），即当P=R时的取值，平衡点的取值越高，性能更优。

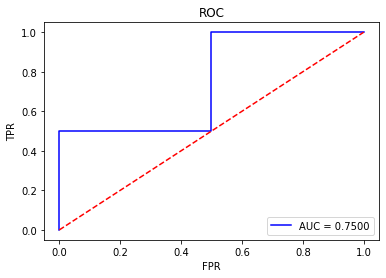
7.ROC曲线（Receiver Operating Characteristic）

ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类别不平衡（Class Imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化，ROC以及AUC可以很好的消除样本类别不平衡对指标结果产生的影响。

ROC曲线分别使用下面两个指标作为X轴和Y轴：

（1）真正率（True Positive Rate , TPR），又称灵敏度（sensitivity）：（其实和召回率一样）

$TPR = \frac{TP}{TP+FN}$

（2）假正率（False Positive Rate , FPR），又称特异度（specificity）：

$FPR = \frac{FP}{TN+FP}$

8.AUC（Area Under Curve）

曲线下面积，是处于ROC Curve下方的那部分面积的大小。对于ROC曲线下方面积越大表明模型性能越好，于是AUC就是由此产生的评价指标。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了模型较好的性能。

import matplotlib.pyplot as plt 
import numpy as np
from sklearn import metrics
y_true = np.array([1, 1, 2, 2])
y_score = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = metrics.roc_curve(y_true, y_score, pos_label=2) 
auc=metrics.auc(fpr, tpr)

plt.title('ROC')
plt.plot(fpr, tpr,'b',label='AUC = %0.4f'% auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')

参考：【机器学习】一文读懂分类算法常用评价指标

Task02-Task05:

数据探索性分析
特征工程
建模与调参
模型融合

notebook已上传到GitHub仓库，线上成绩为0.7360，仍需继续努力。