0%

算法基础（1）

发表于 更新于 分类于 本文字数： 4.3k
开个新坑( ･´ω`･ )，算法基础系列用来记录自己在Acwing上学习和刷题的过程。Acwing算法基础第一章的内容：快速排序，归并排序，二分查找。

开个新坑( ･´ω`･ )，算法基础系列用来记录自己在Acwing上学习和刷题的过程。共勉。

第一章 基础算法

快速排序

算法1：快速排序

快排用到了分治的思想，对一个下标左边界为$l$，下标右边界为$r$的数组，进行快速排序一般可以分为三个步骤：

其中最关键的是第二步-调整区间。暴力做法虽然时间复杂度是常数，但空间占用比较多（需要开额外的数组）。下面是优化后的方法：

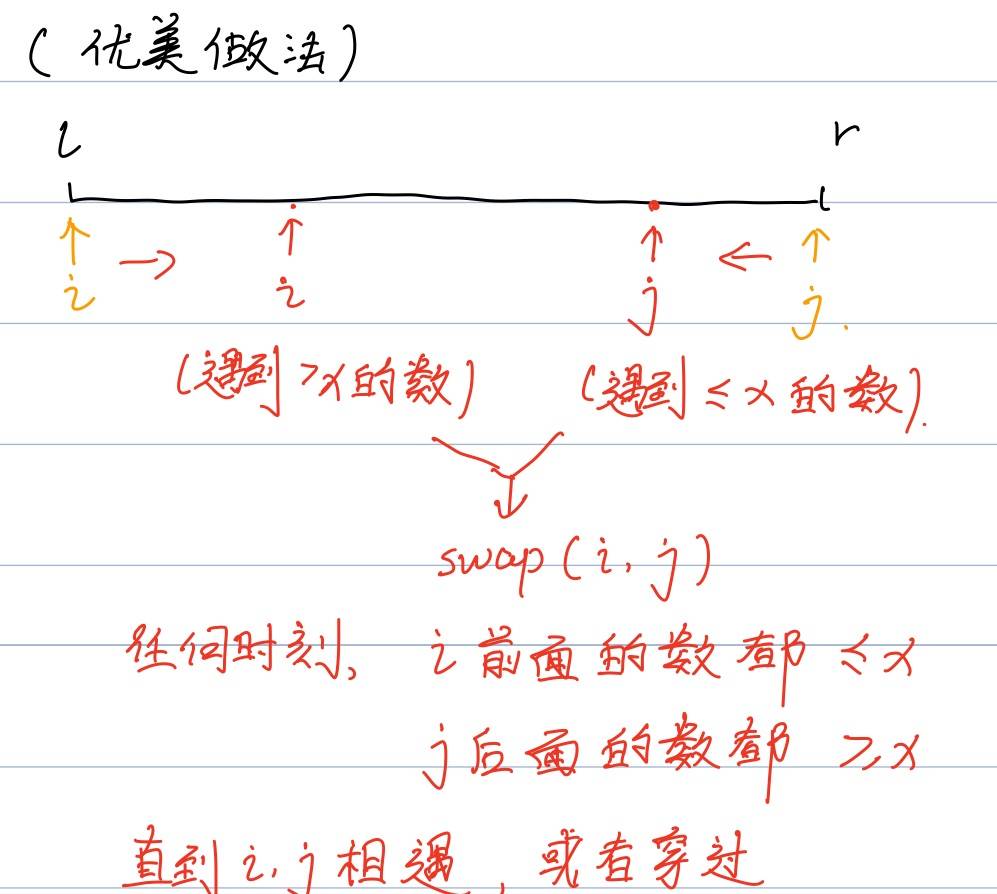
在解题中为了避免在处理边界问题上浪费太多时间，可以记一些快排的模板。

  • 快排模板题：给定你一个长度为$n$的整数数列。请你使用快速排序对这个数列按照从小到大进行排序。并将排好序的数列按顺序输出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N];

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    
    int x = q[l + r >> 1];   // x = q[l]，题目的数据加强过，写成x = q[l]会超时
    int i = l - 1, j = r + 1;   //先把i, j往外移一位。因为后面要先移位再判断
    while(i < j)
    {
        do i++; while(q[i] < x);
        do j--; while(q[j] > x);
        if(i < j)  swap(q[i], q[j]);
    }
    
    quick_sort(q, l, j);
    quick_sort(q, j+1, r);
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++)  scanf("%d", &q[i]);
    
    quick_sort(q, 0, n-1);
    
    for(int i = 0; i < n; i++)  printf("%d ", q[i]);
    return 0;
    
}

快速排序的时间复杂度和空间复杂度：

分析和证明过程可以参考：【算法】快速排序

时间复杂度 空间复杂度
最优 $O(n\log n)$ $O(\log n)$
最坏 $O(n^2)$ $O(n)$
平均 $O(n\log n)$ $O(\log n)$

  • 扩展题：快速选择。

    第$k$个数：给定一个长度为$n$的整数数列，以及一个整数$k$，请用快速选择算法求出数列从小到大排序后的第$k$个数。

    数据范围：$1 \le n \le 100000$，$1 \le k \le n$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;

const int N = 100010;
int n, k;
int q[N];

//快速选择，时间复杂度O(2n)
int quick_sort(int l, int r, int k)
{
    if(l >= r) return q[l];
    int x = q[l + r >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        while( q[ ++ i] < x);
        while( q[ -- j] > x);
        if( i < j )  swap(q[i], q[j]);
    }
    int sl = j - l + 1;
    if( k <= sl ) return quick_sort(l, j, k);
    
    return quick_sort(j + 1, r, k - sl);
}

int main()
{
    scanf("%d%d", &n, &k);
    for(int i = 0; i < n; i++)  scanf("%d", &q[i]);
    
    cout << quick_sort(0, n - 1, k);
    return 0;
}

归并排序

算法2：归并排序

归并排序也用到了分治的思想，通常有三个步骤：

归并排序中最关键的是第三步—归并，可以使用双指针，使时间复杂度为$O(n)$。

  • 归并排序模板题：给定你一个长度为$n$的整数数列。请你使用归并排序对这个数列按照从小到大进行排序。并将排好序的数列按顺序输出。

    数据范围：$1 \le n \le 100000$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<iostream>
using namespace std;
const int N = 100010;
int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    
    int mid = l + r >> 1;
    merge_sort(q, l, mid);
    merge_sort(q, mid+1, r);
    
    int k = 0, i = l, j = mid+1;
    while(i <= mid && j <= r)
        if(q[i] < q[j])  tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];
    
    for(i = l, j = 0; i <= r; i++, j++)
        q[i] = tmp[j];
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++) scanf("%d", &q[i]);
    
    merge_sort(q, 0, n-1);
    
    for(int i = 0; i < n; i++) printf("%d ", q[i]);
    return 0;
}

  • 扩展题：逆序数对的数量

    给定一个长度为$n$的整数数列，请你计算数列中的逆序对的数量。逆序对的定义如下：对于数列的第 $i$ 个和第 $j$ 个元素，如果满足 $i < j $且 $a[i] > a[j]$，则其为一个逆序对；否则不是。

    数据范围：$1 \le n \le 100000$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
using namespace std;

typedef long long LL;

const int N = 100010;
int n;
int q[N], tmp[N];

LL merge_sort(int q[], int l, int r)
{
    if(l >= r)  return;
    int mid = l + r >> 1;
    LL res = merge_sort(q, l, mid) + merge_sort(q, mid + 1, r);

    //归并的过程
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j])    tmp[K ++] = q[i ++];
        else
        {
            tmp[k ++] = q[j ++];
            res += mid - i + 1;
        }
    }
    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];

    for(i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
    return res;
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i++)  scanf("%d", &q[i]);

    cout << merge_sort(q, 0, n - 1) << endl;
    return 0;
}

二分查找

算法3：二分查找

  • 整数的二分查找

例题：给定一个按照升序排列的长度为n的整数数组，以及 q 个查询。对于每个查询，返回一个元素k的起始位置和终止位置（位置从0开始计数）。如果数组中不存在该元素，则返回“-1 -1”。

数据范围：$1 \le n \le 100000$，$1 \le q \le 10000$，$1 \le k \le 10000$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<iostream>
using namespace std;

const int N = 100010;
int n, m;
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i++) scanf("%d", &q[i]);
    while(m--)
    {
        int x;
        scanf("%d", &x);
        
        //查找x的左边界，性质是左边界 右面的数都大于等于x
        int l = 0, r = n-1;
        while(l < r)
        {
            int mid = l + r >> 1;
            if(q[mid] >= x)  r = mid;
            else l = mid + 1;
        }
        if(q[l] != x)  cout << "-1 -1" << endl;   //判断题目是不是无解
        else
        {
            cout << l << " ";    
            //查找x的右边界，性质是右边界 左面的数都小于等于x 
            int l = 0, r = n - 1;
            while(l < r)
            {
                int mid = l + r + 1 >> 1;
                if(q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            cout << l << endl;
        }
    }
    return 0;
}
  • 浮点数二分

例题：给定一个浮点数n，求它的三次方根。结果保留6位小数。

数据范围：$-10000 \le n \le 10000$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include<cstdio>

int main()
{
    double x;
    scanf("%lf", &x);
    
    //根据数据范围确定l和r
    double l = -100, r = 100;
    while(r - l > 1e-8)  //通常要比题目要求的精度多2位 
    {
        double mid = (l + r) / 2;
        if(mid * mid * mid >= x) r = mid;
        else l = mid;
    }
    
    printf("%.6lf\n", l);
    return 0;
}