第二章 数据结构
这节课主要讲如何用数组模拟链表,栈与队列。
链表
我们知道链表可以通过结构体+指针来实现,但每次创建一个新节点就要通过new Node; 来实现,这一过程是很慢的,在做笔试题时一般不会采用这样的动态链表的方式,常用的是用数组来模拟链表,又分为两种:
- 单链表,其中在算法题中用的最多的是邻接表,它最主要的应用是存储图和树
- 双链表,主要作用是优化某些问题
关于链表的基础知识可以参考之前写的 Cpp基础(6)结构体与链表
数组模拟单链表:用两个数组e[N]和ne[N],它们通过下标关联起来,下标从0开始,e[i]用来存放第i个节点的值,ne[i]用来存放第i个节点指向的next节点的下标,空节点的下标用-1来表示。
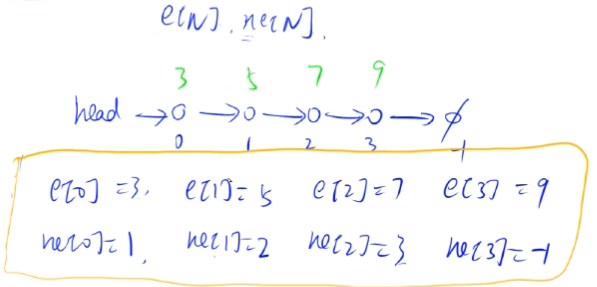
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| #include<iostream>
using namespace std;
const int N = 100010;
int head, e[N], ne[N], idx;
void init()
{
head = -1;
idx = 0;
}
void add_to_head(int x)
{
e[idx] = x, ne[idx] = head, head = idx ++;
}
void add(int k, int x)
{
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++;
}
void remove(int k)
{
ne[k] = ne[ne[k]];
}
int main()
{
int m;
cin >> m;
init();
while( m-- )
{
int k, x;
char op;
cin >> op;
if(op == 'H')
{
cin >> x;
add_to_head(x);
}
else if(op == 'D')
{
cin >> k;
if(!k) head = ne[head];
remove(k - 1);
}
else
{
cin >> k >> x;
add(k - 1, x);
}
}
for(int i = head; i != -1; i = ne[i]) cout << e[i] << ' ';
cout << endl;
return 0;
}
|
双链表的每个节点有两个指针,一个指向前面的点 ,一个指向后面的点,用数组l[]存放节点左边的点的下标,用数组r[]存放节点右边的点的下标。这里我们偷个懒,让下标是0的点是head,让下标是1的点是tail。
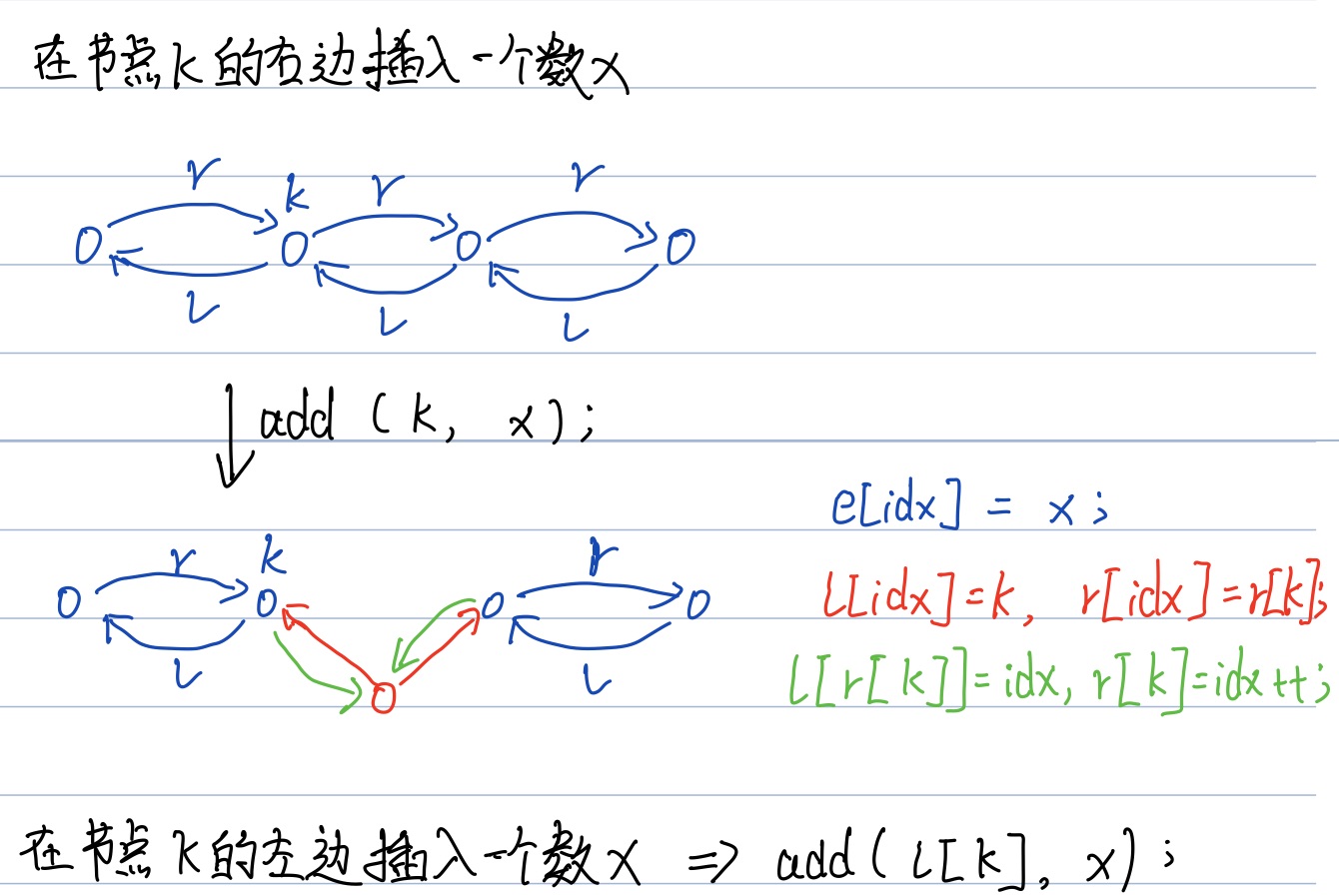
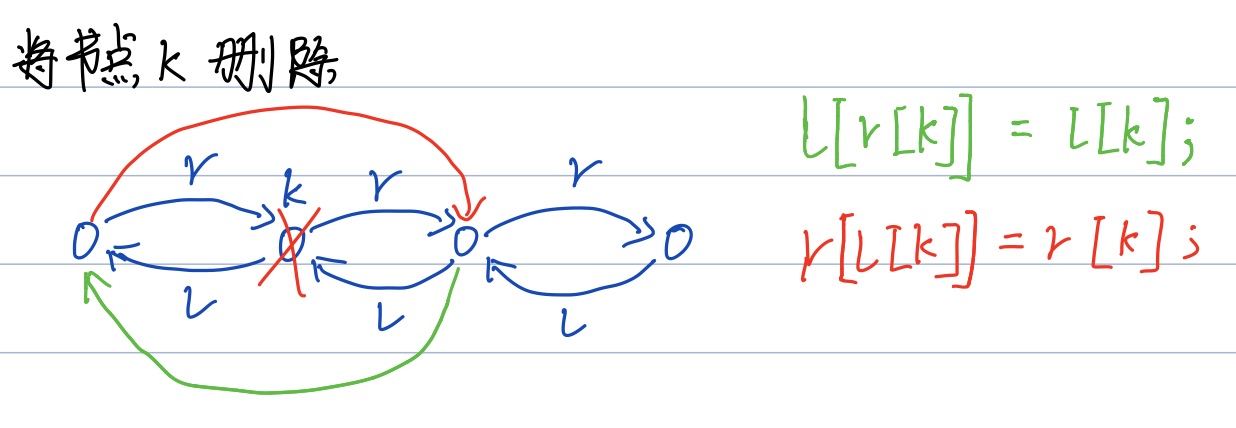
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include<iostream>
using namespace std;
const int N = 100010;
int e[N], l[N], r[N], idx;
void init()
{
r[0] = 1, l[1] = 0;
idx = 2;
}
void add(int k, int x)
{
e[idx] = x;
l[idx] = k, r[idx] = r[k];
l[r[k]] = idx, r[k] = idx ++;
}
void remove(int k)
{
r[l[k]] = r[k];
l[r[k]] = l[k];
}
int main()
{
int m;
cin >> m;
init();
while(m --)
{
string op;
cin >> op;
int k, x;
if(op == "L")
{
cin >> x;
add(0, x);
}
else if(op == "R")
{
cin >> x;
add(l[1], x);
}
else if(op == "D")
{
cin >> k;
remove(k + 1);
}
else if(op == "IL")
{
cin >> k >> x;
add(l[k + 1], x);
}
else
{
cin >> k >> x;
add(k + 1, x);
}
}
for(int i = r[0]; i != 1; i = r[i]) cout << e[i] << ' ';
cout << endl;
return 0;
}
|
栈与队列
栈与队列的基础知识可以参考之前写的 数据结构与算法(7)栈与队列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
const int N = 100010;
int stk[N], tt;
stk[ ++ tt] = x;
tt --;
if(tt > 0) not empty;
else empty;
stk[tt];
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
int q[N], hh, tt = -1;
q[ ++ tt] = x;
hh ++;
if(hh <= tt) not empty;
else empty;
q[hh];
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include<iostream>
using namespace std;
const int N = 100010;
int m;
int stk[N], tt;
int main()
{
cin >> m;
while(m --)
{
string op;
int x;
cin >> op;
if(op == "push")
{
cin >> x;
stk[++ tt] = x;
}
else if(op == "pop") tt --;
else if(op == "empty") cout << (tt ? "NO" : "YES") << endl;
else cout << stk[tt] << endl;
}
return 0;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include<iostream>
using namespace std;
const int N = 100010;
int m;
int q[N], hh, tt = -1;
int main()
{
cin >> m;
while(m --)
{
string op;
int x;
cin >> op;
if(op == "push")
{
cin >> x;
q[++ tt] = x;
}
else if(op == "pop") hh ++;
else if(op == "empty") cout << (hh <= tt ? "NO" : "YES") << endl;
else cout << q[hh] << endl;
}
return 0;
}
|
单调栈与单调队列
单调栈的常见题型:给定一个序列,求序列中每一个数左边离它最近的且比它小的数是多少。
- 例题:给定一个长度为N的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出-1。
保证栈中的数是单调递增的,遍历数列中的数,对于数列中第i个数,若栈非空且栈顶元素大于等于它,就弹出栈顶,直到栈顶比它小,则栈顶即为所求;若栈空,说明不存所求。之后再把第i个数存入栈顶。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include<iostream>
using namespace std;
const int N = 100010;
int stk[N], tt;
int main()
{
int n;
cin >> n;
while(n --)
{
int x;
cin >> x;
while(tt && stk[tt] >= x) tt --;
if(tt) cout << stk[tt] << ' ';
else cout << -1 << ' ';
stk[++ tt] = x;
}
return 0;
}
|
对于每个元素,最多只会进栈一次出栈一次,因此时间复杂度为$O(n)$。
单调队列的常见题型:求滑动窗口中的最大值/最小值
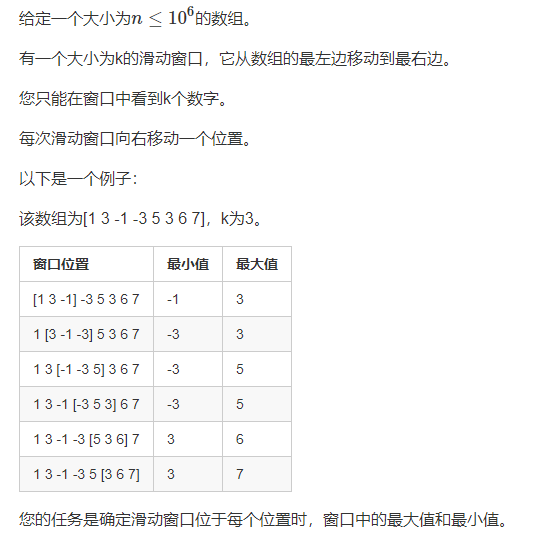

遍历序列中的元素,i表示滑动窗口右端点元素的下标,用一个单调队列来维护当前的滑动窗口,保证队列中的元素是单调递增的,即每插入一个新元素,便判断队尾是否大于等于它,若是就弹出队尾,再把新元素插入队尾,这样每次求滑动窗口中的最小值只需取出队头即可。求滑动窗口中的最大值同理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| #include<iostream>
using namespace std;
int n, k;
const int N = 1000010;
int a[N], q[N];
int main()
{
scanf("%d%d", &n, &k);
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
int hh = 0, tt = -1;
for(int i = 0; i < n; i++)
{
if(hh <= tt && i - k + 1 > q[hh]) hh++;
while(hh <= tt && a[q[tt]] >= a[i]) tt--;
q[++ tt] = i;
if(i >= k - 1) printf("%d ", a[q[hh]]);
}
puts("");
hh = 0, tt = -1;
for(int i = 0; i < n; i++)
{
if(hh <= tt && i - k + 1 > q[hh]) hh++;
while(hh <= tt && a[q[tt]] <= a[i]) tt--;
q[++ tt] = i;
if(i >= k - 1) printf("%d ", a[q[hh]]);
}
puts("");
return 0;
}
|
用单调栈或者单调队列解题的思路都是:先用暴力做法求解,再考虑暴力做法的栈或队列中哪些元素是没有用的,删掉这些没用的元素,再看剩下的元素有没有单调性,如果有就可以考虑用栈或队列做优化。
KMP
给定一个模式串S(长度为M),以及一个模板串P(长度为N),所有字符串中只包含大小写英文字母以及阿拉伯数字。模板串P在模式串S中多次作为子串出现。求出模板串P在模式串S中所有出现的位置的起始下标。
数据范围:$1 \le N \le 10^5$,$1 \le M \le 10^6$。
KMP算法的知识可以参考之前写的 数据结构与算法(20)串——3.KMP算法
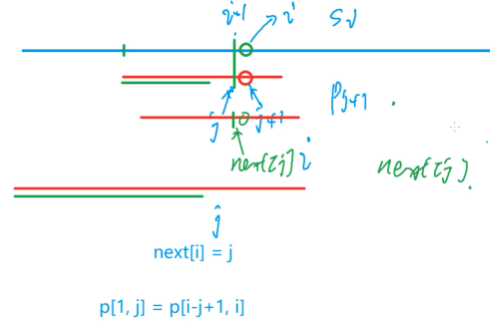
对于模板串要处理出一个:它的一个以第i个元素为右端点的后缀和一个前缀相等,相等的最大长度是多少。如next[i]=j,则说明p[1,j]=p[i-j+1]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| #include<iostream>
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
char p[N], s[M];
int ne[N];
int main()
{
cin >> n >> p + 1 >> m >> s + 1;
for(int i = 2, j = 0; i <= n; i++)
{
while(j && p[i] != p[j + 1]) j = ne[j];
if(p[i] == p[j + 1]) j++;
ne[i] = j;
}
for(int i = 1, j = 0; i <= m; i++)
{
while(j && s[i] != p[j + 1]) j = ne[j];
if(s[i] == p[j + 1]) j++;
if(j == n)
{
printf("%d ", i - n);
j = ne[j];
}
}
return 0;
}
|





